
世界は、多数の解決策が問題は二次方程式の根を見つけることに還元されます。方程式の根は、さまざまなパターンを記述するために重要です。これは古代バビロンの土地測量士にも知られていました。天文学者やエンジニアもそのような問題を解決することを余儀なくされました。西暦6世紀に、インドの科学者アーリヤバタは2次方程式の根を見つけるための基礎を開発しました。公式は19世紀に完成した外観になりました。
二次方程式の基本法則をよく理解しておくことをお勧めします。一般的に、平等は次のように書くことができます。
斧2 + bx + c = 0、
二次方程式の根の数は、1つまたは2つにすることができます。判別式の概念を使用して、簡単な分析を行うことができます。
D = b2 -4ac
計算値に応じて、次のようになります。
注:判別式が負の場合、方程式には実数の範囲にのみ根がありません。代数が複素数の根の概念に拡張された場合、方程式には解があります。
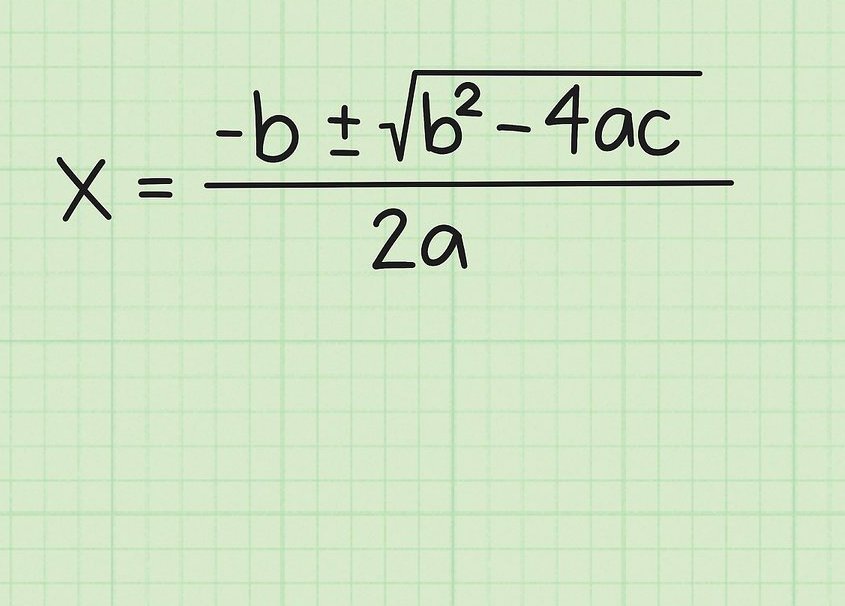
これは、根を見つけるための公式を確認する一連のアクションです。
方程式の一般的な形式から、次のようになります。
斧2 + bx = -c
右側と左側に4aを掛け、bを足します2、 我々が得る
4a2バツ2 + 4abx + b2 = -4ac + b2
左側を平方多項式(2ax + b)として変換します2..。方程式の両辺の平方根を取ります2ax + b = -b±√(-4ac + b2)、係数bを右側に転送すると、次のようになります。
2ax = -b±√(-4ac + b2)
これは、次のことを意味します。
x =(-b±√(b2 -4ac))
表示する必要があるもの。
場合によっては、問題の解決を簡略化できます。したがって、係数bが偶数の場合、より単純な式が得られます。
k = 1 / 2bと表すと、2次方程式の根の一般式は次の形式になります。
x =(-k±√(k2 --ac))/ a
D = 0の場合、x = -k / aが得られます。
もう1つの特殊なケースは、a = 1の方程式の解です。
ビューxの場合2 + bx + c = 0根はx = -k±√(k2 --c)判別式が0より大きい場合。D= 0の場合、ルートは次の簡単な式で決定されます:x = -k。
誰もがそれを知らなくても、二次関数によってよく説明される物理的、化学的、生物学的、さらには社会的現象に常に直面しています。
注:2次関数に基づく曲線は、放物線と呼ばれます。
下記は用例です。

放物線関数の重要性を理解し、「判別式」と「二次方程式の根」の概念を使用して、グラフを使用してその特性を調べる方法を理解しましょう。
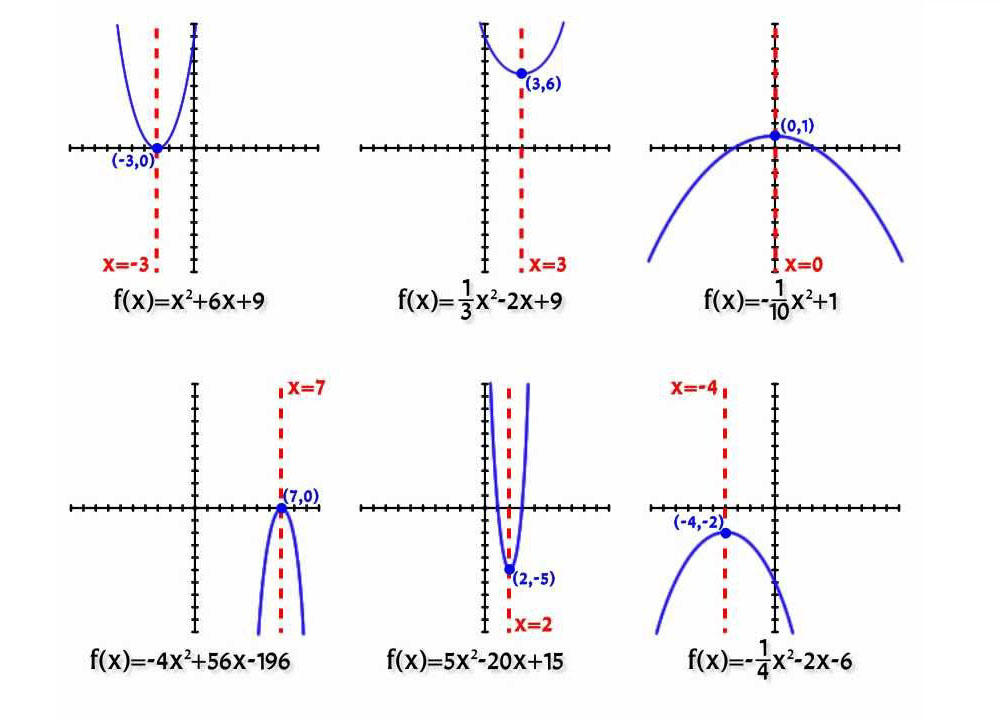
係数aとbの値に応じて、曲線の位置には6つのオプションしかありません。
注:この場合、放物線は直線に縮退するため、オプションa = 0は考慮されません。
上記のすべては、下の図でよく示されています。
条件:一般的なプロパティを使用して、根が互いに等しい2次方程式を作成します。
決定:
問題の条件によってx1 = x2、または-b +√(b2 -4ac)/(2a)= -b +√(b2 -4ac)/(2a)。エントリの簡略化:
-b +√(b2 -4ac)/(2a)-(-b-√(b2 --4ac)/(2a))= 0、角かっこを開き、同様の用語を指定します。方程式は2√(b2 --4ac)= 0。このステートメントは、bの場合に当てはまります。2 -4ac = 0、したがってb2 = 4acの場合、値b =2√(ac)が式に代入されます
斧2 +2√(ac)x + c = 0、誘導型でxを取得します2 +2√(c / a)x + c = 0。
答え:
aが0に等しくなく、任意のcの場合、b =2√(c / a)の場合の解は1つだけです。

すべての単純さのための二次方程式工学計算において非常に重要です。ほとんどすべての物理プロセスは、n次のべき乗則関数を使用した近似で記述できます。二次方程式は、そのような最初の近似になります。
