
Historien til Pythagorean teorem har flereårtusener. Påstanden om at kvadratet på hypotenusen er lik summen av kvadratene på bena, var kjent lenge før fødselen av den greske matematikeren. Imidlertid er Pythagorean-teoremet, skapelsens historie og bevisene for de fleste forbundet med denne forskeren. Ifølge noen kilder var årsaken til dette det første beviset på teoremet, som ble gitt av Pythagoras. Noen forskere tilbakeviser dette faktum.

Før du forteller hvordan historienPythagorean teorem, kort dvele ved biografien til en matematiker. Han levde i VI århundre f.Kr. Fødselsdato for Pythagoras anses å være 570 f.Kr. e., stedet er øya Samos. Lite er kjent om vitenskapsmannens liv. Biografiske data fra gamle greske kilder er sammenvevd med åpenbar fiksjon. På sidene i avhandlingene ser han ut til å være en stor vismann, og mestrer ordet og evnen til å overbevise. Forresten, det er derfor den greske matematikeren fikk kallenavnet Pythagoras, det vil si “overbevisende tale”. I følge en annen versjon ble fødselen til fremtidens vismann spådd av Pythia. Faren hennes het gutten Pythagoras.

Vismannen lærte av datidens store sinn.Blant lærerne til de unge Pythagorasene er Germodamant og Feriqid fra Syros. Den første innpodet en kjærlighet til musikk, den andre lærte filosofi. Begge disse vitenskapene vil forbli i sentrum av oppmerksomheten til forskeren hele livet.
По одной из версий, будучи пытливым юношей, Pythagoras forlot hjemlandet. Han dro for å søke kunnskap i Egypt, der han ifølge forskjellige kilder bodde fra 11 til 22 år gammel, og ble deretter tatt til fange og sendt til Babylon. Pythagoras kunne dra nytte av sin stilling. I 12 år studerte han matematikk, geometri og magi i en eldgammel tilstand. Pythagoras kom tilbake til Samos først ved 56 år gammel. Her styrte tyrannpolitiene på den tiden. Pythagoras kunne ikke godta et slikt politisk system og dro snart til Sør-Italia, der den greske kolonien Croton lå.
I dag er det umulig å si sikkert om Pythagoras var i Egypt og Babylon. Kanskje forlot han Samos senere og dro rett til Croton.

Historien til Pythagorean teorem er relatert til utviklingen avopprettet av den greske filosofskolen. Denne religiøse og etiske brorskap forkynte en spesiell livsstil, studerte aritmetikk, geometri og astronomi, studerte de filosofiske og mystiske aspektene ved tall.
Все открытия учеников греческого математика tilskrevet ham. Historien om fremveksten av Pythagorean teorem er imidlertid assosiert av eldgamle biografier bare med filosofen selv. Det antas at han overførte kunnskapene til Babylon og Egypt til grekerne. Det er også en versjon om at han virkelig oppdaget et teorem om forholdet mellom ben og hypotenuse, uten å vite om prestasjonene til andre nasjoner.
I noen gamle greske kildergleden ved Pythagoras beskrives da han var i stand til å bevise teoremet. Til ære for en slik begivenhet beordret han et offer til gudene i form av hundre okser og holdt en høytid. Noen lærde peker imidlertid på umuligheten av en slik handling på grunn av særegenhetene i de pythagoreiske synspunktene.
Det antas at i avhandlingen "Begynnelser", opprettetEuclid, forfatteren gir et bevis på teorem, hvis forfatter var den store greske matematikeren. Dette synet ble imidlertid ikke støttet av alle. Dermed påpekte den eldgamle ny-platoniske filosofen Proclus at forfatteren av beviset gitt i "Elementene" er Euklid selv.
Det var som det kan, men den første som formulerte teoremet var fremdeles ikke Pythagoras.

Pytagoreisk teorem hvis skapelseshistoriebetraktet i artikkelen, ifølge den tyske matematikeren Cantor, var kjent så langt tilbake som 2300 f.Kr. e. i Egypt. De gamle innbyggerne i Nildalen under Farao Amenemkets regjering kjente jeg til likhet 32 + 4² = 5². Det antas at ved hjelp av trekanter med sidene 3, 4 og 5 bygde de egyptiske “taustrammerne” rette vinkler.
De kjente det pytagoreiske teoremet i Babylon.På levertabletter fra 2000 f.Kr. og dateres tilbake til kong Hammurabis regjering, ble en omtrentlig beregning av hypotenusen til en høyre trekant oppdaget.
Historien til Pythagorean teorem er knyttet til det gamlesivilisasjoner i India og Kina. Avhandlingen "Zhou-bi Xuan Jin" inneholder indikasjoner på at den egyptiske trekanten (dens sider tilsvarer 3: 4: 5) var kjent i Kina på XII-tallet. BC e., og til VI århundre. BC e. matematikere i denne staten kjente til den generelle teoremformen.
Konstruksjonen av den rette vinkelen ved hjelp av den egyptiske trekanten ble også beskrevet i den indiske avhandlingen "Sulva Sutra", som stammer fra det 7. og 5. århundre. BC e.
Dermed var historien til Pythagorean teorem ved fødselen av den greske matematikeren og filosofen i flere hundre år.
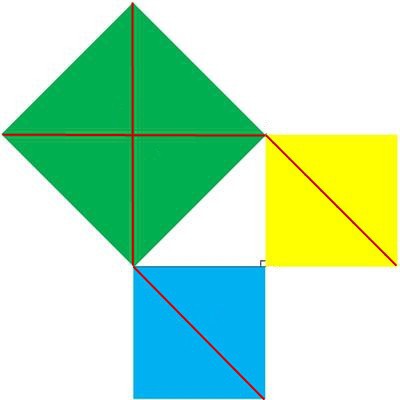
I løpet av dens eksistens har teorem blitt ettfra grunnleggende innen geometri. Historien om beviset på Pythagorean-teoremet begynte antagelig med en betraktning av en liksidig høyre trekant. På hypotenusen og bena hans er firkanter bygget. Den som "vokste opp" på hypotenusen vil bestå av fire trekanter lik den første. Kvadratene på beina består i dette tilfellet av to slike trekanter. Et enkelt grafisk bilde viser tydelig gyldigheten av utsagnet formulert i form av det berømte teoremet.
Nok et enkelt bevis kombinerergeometri med algebra. Fire identiske rettvinklede trekanter med sidene a, b, c er tegnet slik at de danner to firkanter: den ytre med siden (a + b) og den indre med siden c. I dette tilfellet vil området til det mindre torget være lik2. Det store arealet er beregnet ut fra summen av områdene til det lille torget og alle trekanter (arealet av en rettvinklet trekant, tilbakekalling, beregnes med formelen (a * c) / 2), dvs. med2 + 4 * ((a * b) / 2), som er lik2 + 2av. Arealet til et stort kvadrat kan beregnes på en annen måte - som et produkt av to sider, det vil si (a + c)2som er lik a2 + 2av + c2. Det viser seg:
og2 + 2av + c2 = s2 + 2av,
og2 + inn2 = s2.
Det er mange alternativer for å bevise dette.teoremer. Euclid og indiske forskere, og Leonardo da Vinci arbeidet med dem. Ofte hadde eldgamle vismenn med seg tegninger, eksempler som er plassert over, og fulgte ikke med noen forklaringer, bortsett fra notatet "Se!" Enkelheten av det geometriske beviset, forutsatt at det var viss kunnskap om kommentarene, var ikke nødvendig.
Historien om Pythagorean teorem, oppsummert iartikkelen, hvor jeg myter om dens opprinnelse. Imidlertid er det vanskelig å til og med forestille seg at navnet på den store greske matematikeren og filosofen en dag vil slutte å bli assosiert med det.


























