
Štúdium procesov vyskytujúcich sa v štatistikesystémy komplikované minimálnou veľkosťou častíc a ich obrovským počtom. Je prakticky nemožné uvažovať o každej častici osobitne, preto sa zavádzajú štatistické množstvá: priemerná rýchlosť častíc, ich koncentrácia, hmotnosť častice. Vzorec charakterizujúci stav systému s prihliadnutím na mikroskopické parametre sa nazýva základná rovnica molekulárnej kinetickej teórie plynov (MKT).
Ako prvé bolo stanovené rýchlosť pohybu častícvykonávané experimentálne. Experiment známy zo školských osnov, ktorý uskutočnil Otto Stern, umožnil vytvoriť predstavu o rýchlosti častíc. V priebehu experimentu sa skúmal pohyb atómov striebra v rotujúcich valcoch: najskôr v stacionárnom stave zariadenia, potom, keď sa otáčal s určitou uhlovou rýchlosťou.
Ako výsledok sa zistilo, že rýchlosť molekúlstriebro presahuje rýchlosť zvuku a je 500 m / s. Táto skutočnosť je celkom zaujímavá, pretože pre človeka je ťažké cítiť také rýchlosti pohybu častíc v látkach.
Zdá sa, že je možné pokračovať vo výskumeiba v systéme, ktorého parametre je možné určiť priamym meraním pomocou fyzikálnych prístrojov. Rýchlosť sa meria rýchlomerom, ale myšlienka pripevniť rýchlomer k jednej častici je absurdná. Priamo sa môžu merať iba makroskopické parametre spojené s pohybom častíc.
Akýkoľvek systém vzájomne pôsobiacich teliescharakterizovaná potenciálnou energiou a kinetickou energiou pohybu. Skutočný plyn je komplexný systém. Variabilita potenciálnej energie nie je vhodná na systematizáciu. Problém je možné vyriešiť zavedením modelu, ktorý nesie charakteristické vlastnosti plynu, pričom sa odstráni zložitosť interakcie.
Ideálny plyn je stav hmoty, v ktorominterakcia častíc je zanedbateľná, potenciálna energia interakcie má tendenciu k nule. Za významnú možno považovať iba energiu pohybu, ktorá závisí od rýchlosti častíc.

Odhaľte vzťah medzi tlakom plynu a rýchlosťoupohyb jeho častíc umožňuje základnú rovnicu MKT ideálneho plynu. Častica pohybujúca sa v nádobe po zrážke so stenou do nej prenáša impulz, ktorého hodnotu je možné určiť na základe Newtonovho zákona II:
Zmena hybnosti častice počas pružného nárazu je spojená so zmenou horizontálnej zložky jej rýchlosti. F je sila pôsobiaca z častice na stenu na krátky čas t; m0 Je hmotnosť častice.
Všetky častice plynu pohybujúce sa v smere povrchu rýchlosťou vs a umiestnené vo valci objemu SυsΔt. Keď je koncentrácia častíc n, presne polovica molekúl sa pohybuje smerom k stene, druhá polovica v opačnom smere.
Po zvážení zrážky všetkých častíc môžeme napísať Newtonov zákon pre silu pôsobiacu na miesto:
Pretože tlak plynu je definovaný ako pomer sily pôsobiacej kolmo na povrch k jeho ploche, môžeme napísať:
Výsledný vzťah ako základná rovnica MKT nemôže opísať celý systém, pretože do úvahy prichádza iba pohyb v jednom smere.
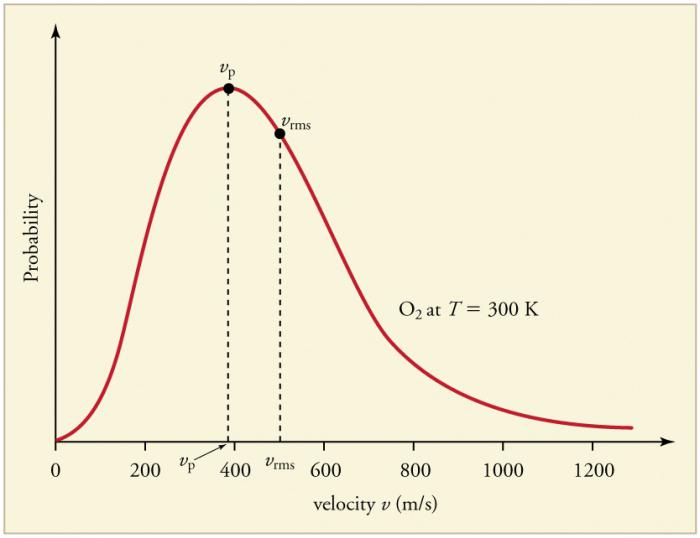
Neustále časté zrážky plynných častíc ssteny a navzájom vedú k vytvoreniu určitého štatistického rozloženia častíc cez rýchlosti (energie). Smery všetkých vektorov rýchlosti sú rovnako pravdepodobné. Táto distribúcia sa nazýva Maxwellova distribúcia. V roku 1860 tento vzorec odvodil J. Maxwell na základe MKT. Hlavné parametre distribučného zákona sa nazývajú rýchlosti: pravdepodobné, zodpovedajúce maximálnej hodnote krivky, a rms vštvorcový = √ ‹v2›Je priemer zo štvorca rýchlosti častíc.
Zvýšenie teploty plynu zodpovedá zvýšeniu hodnoty rýchlostí.
Na základe skutočnosti, že všetky rýchlosti sú rovnaké a ich moduly majú rovnakú hodnotu, môžeme zvážiť:
Základná rovnica MKT, ktorá zohľadňuje priemernú hodnotu tlaku plynu, má tvar:
Tento pomer je jedinečný v tom, že určuje vzťah medzi mikroskopickými parametrami: rýchlosťou, hmotnosťou častíc, koncentráciou častíc a tlakom plynu vo všeobecnosti.
Pomocou konceptu kinetickej energie častíc je možné základnú rovnicu MKT prepísať inak:
Tlak plynu je úmerný priemernej kinetickej energii jeho častíc.
Je zaujímavé, že pre konštantné množstvo plynu vuzavretá nádoba, môžete porovnať tlak plynu a priemernú hodnotu energie pohybu častíc. V tomto prípade môže byť meranie tlaku uskutočnené meraním energie častíc.
Ako postupovať? Aké množstvo je možné porovnať s kinetickou energiou? Táto hodnota sa ukáže ako teplota.


Zaujímavejšie z pohľadu nezávislosti odvlastnosti pracovnej tekutiny možno považovať za plynové teplomery. Ich rozsah je nezávislý na type použitého plynu. V takom zariadení je možné hypoteticky zvoliť teplotu, pri ktorej má tlak plynu tendenciu k nule. Výpočty ukazujú, že táto hodnota zodpovedá -273,15 oS.Teplotná stupnica (stupnica absolútnej teploty alebo Kelvinova stupnica) bola zavedená v roku 1848. Za hlavný bod tejto stupnice sa považovala možná teplota nulového tlaku plynu. Jednotkový segment stupnice sa rovná jednotkovej hodnote stupňov Celzia. Pri štúdiu plynových procesov je pohodlnejšie napísať základnú rovnicu MKT pomocou teploty.
Empiricky sa môžete uistiť, že tlak plynu je úmerný jeho teplote. Zároveň sa zistilo, že tlak je priamo úmerný koncentrácii častíc:
kde Т - absolútna teplota, k -konštanta sa rovná 1,38 • 10-23J / K.
Základná veličina, ktorá má pre všetky plyny konštantnú hodnotu, sa nazýva Boltzmannova konštanta.
Porovnaním závislosti tlaku na teplote a základnej rovnice MKT plynov môžeme napísať:
Priemerná hodnota kinetickej energie pohybu molekúl plynu je úmerná jej teplote. To znamená, že teplota môže slúžiť ako miera kinetickej energie pohybu častíc.


























