
Трапез је посебан случај четвороугла, ичији је један пар страница паралелан. Израз "трапез" потиче од грчке речи τραπεζα, што значи "сто", "сто". У овом чланку ћемо погледати врсте трапеза и његове особине. Осим тога, смислићемо како израчунати појединачне елементе ове геометријске фигуре. На пример, дијагонала једнакокраког трапеза, средишња линија, површина итд. Материјал је представљен у стилу елементарне популарне геометрије, односно у лако доступном облику.
Прво, хајде да схватимо шта јечетвороугао. Овај облик је посебан случај полигона са четири стране и четири темена. Два врха четвороугла који нису суседни називају се супротним. Исто се може рећи за две стране које нису суседне. Главни типови четвороуглова су паралелограм, правоугаоник, ромб, квадрат, трапез и делтоид.

Дакле, назад на трапезоиде.Као што смо рекли, ова фигура има две стране паралелне. Зову се базе. Друге две (непаралелне) су странице. У материјалима испита и различитих тестова врло често можете пронаћи задатке везане за трапезије, чије решење често захтева од студента знање које није предвиђено програмом. Школски курс геометрије упознаје ученике са својствима углова и дијагонала, као и средњом линијом једнакокраког трапеза. Али поред овога, поменута геометријска фигура има и друге особине. Али о њима нешто касније ...
Постоји много врста ове фигуре. Међутим, најчешће је уобичајено разматрати два од њих - једнакокраке и правоугаоне.
1. Правокутни трапез је фигура у којој је једна од бочних страница окомита на основе. Његова два угла су увек једнака деведесет степени.
2. Једнакокраки трапез је геометријска фигура са једнаким страницама. То значи да су углови на основама такође парно једнаки.

Главни принцип је употребатакозвани приступ задатака. У ствари, нема потребе за увођењем нових својстава ове фигуре у теоријски курс геометрије. Могу се отворити и формулисати у процесу решавања различитих проблема (бољих од системских). Истовремено, веома је важно да наставник зна које задатке треба дати школарцима у једном или другом тренутку образовног процеса. Штавише, свако својство трапеза може се представити као кључни задатак у систему задатака.
Други принцип је тзвспирална организација проучавања "изузетних" својстава трапеза. То подразумева повратак у процесу учења индивидуалним карактеристикама дате геометријске фигуре. Ово олакшава ученицима да их запамте. На пример, својство четири тачке. То се може доказати проучавањем сличности и накнадном употребом вектора. Једнака величина троуглова уз бочне странице фигуре може се доказати применом не само својстава троуглова једнаких висина повучених на странице које леже на једној правој линији, већ и употребом формуле С = 1/2 (аб * синα). Осим тога, можете разрадити теорему синуса на уписаном трапезу или правоуглог троугла на описаном трапезу итд.
Примена функција „ван програма“геометријска фигура у садржају школског предмета представља технологију задатака за њихово поучавање. Стално позивање на проучена својства приликом преношења других тема омогућава студентима дубље разумевање трапеза и обезбеђује успех у решавању додељених задатака. Дакле, пређимо на проучавање ове дивне фигуре.

Као што смо већ приметили, ова геометријскафигуре на страницама су једнаке. Познат је и као правилан трапез. И зашто је тако изванредан и зашто је добио тако име? Посебности ове фигуре укључују чињеницу да има једнаке не само странице и углове у основама, већ и дијагонале. Осим тога, збир углова једнакокраког трапеза је 360 степени. Али то није све! Од свих познатих трапеза, само око једнакокраког може се описати круг. То је због чињенице да је збир супротних углова ове фигуре 180 степени, а само под овим условом може се описати круг око четвороугла. Следеће својство разматране геометријске фигуре је да ће растојање од врха основе до пројекције супротног темена на праву линију која садржи ову основу бити једнако средишњој линији.
Хајде сада да схватимо како да пронађемо углове једнакокраког трапеза. Размотрите решење овог проблема, под условом да су познате димензије страница фигуре.
Обично се четвороугао обично означаваслова А, Б, Ц, Д, где су БС и АД базе. У једнакокраком трапезу странице су једнаке. Претпоставићемо да је њихова величина једнака Кс, а величине база једнаке И и З (мање и веће). Да би се извршио прорачун, потребно је извући висину Х из угла Б. Резултат је правоугли троугао АБН, где је АБ хипотенуза, а БН и АН катете. Израчунавамо величину крака АХ: мањи одузимамо од веће основе, а резултат делимо са 2. Пишемо га у облику формуле: (ЗИ) / 2 = Ф. Сада, за израчунавање оштрог угла троугла користимо цос функцију. Добијамо следећи запис: цос (β) = Кс / Ф. Сада израчунавамо угао: β = арцос (Кс / Ф). Даље, познавајући један угао, можемо одредити други, за то изводимо елементарну аритметичку операцију: 180 - β. Сви углови су дефинисани.
Постоји и друго решење овог проблема.На почетку из угла спуштамо висину Н. Израчунајте вредност крака БН. Знамо да је квадрат хипотенузе правоуглог троугла једнак збиру квадрата катета. Добијамо: БН = √ (Кс2-Ф2). Затим користимо тригонометријску функцију тг. Као резултат тога, имамо: β = арктан (БН / Ф). Пронађен је оштар угао. Затим дефинишемо тупи угао на исти начин као у првој методи.
Запишимо прво четири правила. Ако су дијагонале у једнакокраком трапезу окомите, тада:
- висина фигуре биће једнака збиру основа, подељених са два;
- његова висина и средња линија су једнаке;
- површина трапеза биће једнака квадрату висине (средња линија, половина збира основа);
- квадрат дијагонале једнак је половини квадрата збира основа или два пута квадрат средње линије (висине).
Сада размотримо формуле које одређују дијагоналу једнакокраког трапеза. Овај блок информација може се грубо поделити на четири дела:
1. Формула дужине дијагонале у смислу њених страница.
Претпостављамо да је А доња основа, Б врх, Ц једнаке странице, Д дијагонала. У овом случају, дужина се може одредити на следећи начин:
Д = √ (Ц2 + А * Б).
2. Формуле за дужину дијагонале према косинусној теореми.
Прихватамо да је А доња база, Б горња,Ц - једнаке странице, Д - дијагонала, α (на доњој бази) и β (на горњој бази) - трапезоидни углови. Добијамо следеће формуле помоћу којих можете израчунати дужину дијагонале:
- Д = √ (А2 + Ц2-2А * Ц * цосα);
- Д = √ (А2 + Ц2-2А * Ц * цосβ);
- Д = √ (Б2 + Ц2-2Б * Ц * цосβ);
- Д = √ (Б2 + Ц2-2Б * Ц * цосα).
3. Формуле за дужину дијагонала једнакокраког трапеза.
Претпостављамо да је А доња основа, Б врх, Д дијагонала, М средња линија, Х висина, П површина трапеза, α и β су углови између дијагонала. Дужину одређујемо помоћу следећих формула:
- Д = √ (М2 + Х2);
- Д = √ (Х2 + (А + Б) 2/4);
- Д = √ (Х (А + Б) / синα) = √ (2П / синα) = √ (2М * Х / синα).
У овом случају, једнакост је тачна: синα = синβ.
4. Формуле за дужину дијагонале у смислу страница и висине.
Претпостављамо да је А доња база, Б врх, Ц странице, Д дијагонала, Х висина, α угао при дну основе.
Дужину одређујемо помоћу следећих формула:
- Д = √ (Х2 + (А-П * цтгα) 2);
- Д = √ (Х2 + (Б + П * цтгα) 2);
-Д = √ (А2 + Ц2-2А * √ (Ц2-Х2)).

Погледајмо шта је занимљиво за ову геометријску фигуру. Као што смо рекли, правоугаони трапез има два права угла.
Поред класичне дефиниције, постоје идруго. На пример, правоугаони трапез је трапез чија је једна страна окомита на основе. Или фигура са правим углом на бочној страни. За ову врсту трапеза висина је једнака бочној страни која је окомита на основе. Средња линија је сегмент линије који повезује средине две стране. Својство поменутог елемента је да је паралелно са основицама и једнако половини њиховог збира.
Хајде сада да погледамо основне формуле,дефинисање ове геометријске фигуре. За ово, претпостављамо да су А и Б основе; Ц (окомито на основе) и Д - странице правоугаоног трапеза, М - средња линија, α - оштар угао, П - површина.
1.Бочна страница, окомита на основе, једнака је висини фигуре (Ц = Х) и једнака је производу дужине друге бочне странице Д и синуса угла α са већом основом ( Ц = Д * синα). Осим тога, једнако је производу тангенте оштрог угла α и разлици основа: Ц = (А-Б) * тгα.
2. Бочна страница Д (није окомита на основе) једнака је количнику разлике између А и Б и косинуса (α) оштрог угла или количника висине фигуре Х и синуса оштар угао: Д = (АБ) / цос α = Ц / синα.
3. Страна која је окомита на основе једнака је квадратном корену разлике између квадрата Д - друге бочне странице - и квадрата разлике међу основама:
Ц = √ (Д2- (А-Б) 2).
4. Страна Д правоугаоног трапеза једнака је квадратном корену збира квадрата странице Ц и квадрату разлике између основа геометријске фигуре: Д = √ (Ц2 + (А-Б) 2).
5. Страница Ц је једнака количнику дељења двоструке површине сумом њених основа: Ц = П / М = 2П / (А + Б).
6. Површина је одређена производом М (средња линија правоугаоног трапеза) по висини или бочној страни окомитој на основе: П = М * Х = М * Ц.
7. Страница Ц је једнака количнику дељења удвостручене површине фигуре на производ синуса оштрог угла и збира његових основа: Ц = П / М * синα = 2П / ((А + Б) * синα).
8. Формуле за бочну страницу правоугаоног трапеза кроз његове дијагонале и угао између њих:
- синα = синβ;
- Ц = (Д1 * Д2 / (А + Б)) * синα = (Д1 * Д2 / (А + Б)) * синβ,
где су Д1 и Д2 дијагонале трапеза; α и β су углови између њих.
9. Формуле бочне странице кроз угао на доњој бази и других страница: Д = (А-Б) / цосα = Ц / синα = Х / синα.
Пошто је трапез са правим углом посебан случај трапеза, остале формуле које дефинишу ове фигуре одговараће правокутном.

Ако услов каже да је круг уписан у правоугаони трапез, тада се могу користити следећа својства:
- збир основа једнак је збиру страница;
- растојања од врха правоугаоног облика до додирних тачака уписаног круга су увек једнака;
- висина трапеза једнака је бочној страни, окомита на основе, и једнака пречнику круга;
- центар кружнице је тачка у којој се секу симетрале углова;
- ако је бочна страница додирном тачком подељена на сегменте Х и М, тада је полупречник круга једнак квадратном корену производа ових сегмената;
- четвороугао формиран од додирних тачака, врха трапеза и центра уписане кружнице - ово је квадрат чија је страница једнака полупречнику;
- површина фигуре једнака је производу основа и производу полусума база по његовој висини.
Ова тема је врло погодна за проучавање некретнина.овај геометријски облик. На пример, дијагонале деле трапез на четири троугла, а они уз базе су слични, а странице једнаке. Ова изјава се може назвати својством троуглова на које је трапез подељен својим дијагоналама. Први део ове изјаве доказује се знаком сличности у два угла. Да бисте доказали други део, боље је користити доњу методу.
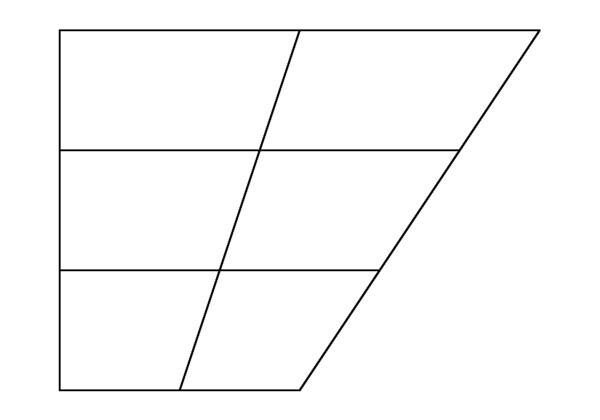
Прихватамо да је цифра АБСД -а (БП и БС основа)трапез) је подељен дијагоналама ВД и АЦ. Тачка њиховог пресека је О. Добијамо четири троугла: АОС - на доњој бази, БОС - на горњој бази, АБО и СОД на бочним страницама. Троуглови СОД и БФБ имају заједничку висину ако су им сегменти БО и ОД базе. Добијамо да је разлика између њихових површина (П) једнака разлици између ових сегмената: ПБОС / ПСОД = БО / ОД = К. Дакле, ПСОД = ПБОС / К. Слично, троуглови БФБ и АОБ имају заједничку висину. За њихове базе узимамо сегменте СБ и ОА. Добијамо ПБОС / ПАОБ = СО / ОА = К и ПАОБ = ПБОС / К. Из овога следи да је ПСОД = ПАОБ.
За учвршћивање градива препоручује се ученицимапронаћи однос између површина насталих троуглова, на које је трапез подељен својим дијагоналама, решавајући следећи проблем. Познато је да су површине трокута биофидбека и АОД једнаке; потребно је пронаћи површину трапеза. Пошто је ПСОД = ПАОБ, то значи да је ПАБСД = ПБОС + ПАОД + 2 * ПСОД. Из сличности троуглова БФБ и АОД следи да је БО / ОД = √ (ПБОС / ПАОД). Према томе, ПБОС / ПСОД = БО / ОД = √ (ПБОС / ПАОД). Добијамо ПСОД = √ (ПБОС * ПАОД). Тада је ПАБСД = ПБОС + ПАОД + 2 * √ (ПБОС * ПАОД) = (√ ПСОС + √ ПАОД) 2.
Настављајући развој ове теме, може се доказати идруге занимљиве карактеристике трапеза. Дакле, уз помоћ сличности може се доказати својство сегмента који пролази кроз тачку насталу пресеком дијагонала ове геометријске фигуре, паралелне са основама. Да бисмо то урадили, решићемо следећи проблем: потребно је пронаћи дужину сегмента РК, који пролази кроз тачку О. Из сличности троуглова АОД и БФБ следи да је АО / ОС = АД / БС . Из сличности троуглова АОР и АСБ следи да је АО / АЦ = РО / БС = ПАКЛО ((БС + ПАКЛО)). Одавде добијамо да је РО = БС * ПАКАО / (БС + ПАКАО). Слично, из сличности троуглова ДОК и ДБС следи да је ОК = БС * ПАКАО / (БС + ПАКАО). Одавде добијамо да је РО = ОК и РК = 2 * БС * ПАКЛО / (БС + ПАКАО). Одсечак који пролази кроз тачку пресека дијагонала, паралелан са основама и повезује две стране, преполовљен је тачком пресека. Његова дужина је хармонијска средина основе фигуре.
Узмите у обзир следећи квалитет трапеза, којиназива се својство четири тачке. Тачке пресека дијагонала (О), пресек продужетка бочних страница (Е), као и средине база (Т и Г) леже увек на истој правој. То се лако доказује методом сличности. Добијени троуглови БЕС и АЕД су слични, а у сваком од њих медијане ЕТ и ЕЗ деле угао при врху Е на једнаке делове. Према томе, тачке Е, Т и Ж леже на једној правој. На исти начин, тачке Т, О и Зх налазе се на једној правој линији, а све то следи из сличности троуглова БФБ и АОД. Из овога закључујемо да ће све четири тачке - Е, Т, О и Ф - лежати на једној правој линији.
Користећи такве трапезе, може се понудитиученици проналазе дужину сегмента (ЛФ), чиме се фигура дели на два слична. Овај сегмент мора бити паралелан са базама. Пошто су добијени трапези АЛПД и ЛБСФ слични, тада је БС / ЛФ = ЛФ / БП. Из тога следи да је ЛФ = √ (БС * ПАКАО). Добијамо да сегмент који дели трапез на два слична има дужину једнаку геометријској средини дужина основа фигуре.
Размотрите следеће својство сличности.Заснован је на сегменту који дели трапез на две фигуре једнаке величине. Претпостављамо да је трапез АБСД подијељен сегментом ЕН на два слична. Из врха Б пада висина која је сегментом ЕХ подељена на два дела - Б1 и Б2. Добијамо: ПАБСД / 2 = (БС + ЕХ) * Б1 / 2 = (ПАКАО + ЕХ) * Б2 / 2 и ПАБСД = (БС + ПАКЛО) * (Б1 + Б2) / 2. Затим састављамо систем чија је прва једначина (БС + ЕХ) * Б1 = (ХЕЛЛ + ЕХ) * Б2 и друга (БС + ЕХ) * Б1 = (БС + ХЕЛЛ) * (Б1 + Б2) / 2. Из тога следи да је Б2 / Б1 = (БС + ЕХ) / (АД + ЕХ) и БС + ЕХ = ((БС + ПАКАО) / 2) * (1 + Б2 / Б1). Добијамо да је дужина сегмента који дели трапез на две једнаке величине једнака корену средње дужине основа: √ ((БС2 + АД2) / 2).
Дакле, доказали смо да:
1. Сегмент који повезује средине бочних страница на трапезу паралелан је са БП и БС и једнак је аритметичкој средини БС и БП (дужина основе трапеза).
2. Права која пролази кроз тачку О пресека дијагонала паралелних са ПАКЛОМ и БС биће једнака хармоничној средини бројева ПАКЛА и БС (2 * БС * ПАКАО / (БС + ПАКАО)).
3. Сегмент који дели трапез на сличне има дужину геометријске средине база БС и БП.
4. Елемент који дели фигуру на две једнаке величине има дужину средњих квадратних бројева БП и БС.
За консолидацију материјала и разумевање везе измеђупроучаване сегменте, студент треба да их изгради за одређени трапез. Он може лако приказати средњу линију и сегмент који пролази кроз тачку О - пресек дијагонала фигуре - паралелне са основама. Али где ће се налазити трећи и четврти? Овај одговор ће довести ученика до откривања жељене везе између просека.
Размотрите следеће својство ове фигуре.Претпостављамо да је сегмент МХ паралелан с основама и дијели дијагонале на пола. Тачке пресека ће се звати Ш и Ш. Овај сегмент ће бити једнак полуразлици основа. Погледајмо ово ближе. МСх - средња линија троугла АБС, једнака је БС / 2. МЦх је средња линија троугла АБД, једнака је БП / 2. Тада добијамо да је СХСХ = МСХ-МСХ, дакле, СХСХ = ПАКАО / 2-БС / 2 = (ПАКЛО + ВС) / 2.
Да видимо како се то одређујеовај елемент за дати геометријски облик. Да бисте то урадили, потребно је проширити базе у супротним правцима. Шта то значи? Доњи је потребно додати горњој бази - на било коју страну, на пример, десно. И продужите доњи за дужину горњег лево. Затим их повезујемо дијагоналом. Тачка пресека овог сегмента са средњом линијом фигуре је тежиште трапеза.
Наведимо карактеристике таквих облика:
1. Трапез се може уписати у круг само ако је једнакокрачан.
2. Трапез се може описати око круга, под условом да је збир дужина њихових база једнак збиру дужина бочних страница.
Последице уписаног круга:
1. Висина описаног трапеза увек је једнака два радијуса.
2. Бочна страна описаног трапеза посматра се из средишта круга под правим углом.
Први закључак је очигледан, али за доказдруго, потребно је утврдити да је угао СОД -а прави, што, у ствари, такође неће бити тешко. Али познавање овог својства ће вам омогућити да користите правоугли троугао при решавању проблема.
Сада конкретизујмо ове последице заједнакокраки трапез који је уписан у круг. Добијамо да је висина геометријска средина основе фигуре: Х = 2Р = √ (БС * ПАКАО). Док вежба основну технику решавања задатака за трапезе (принцип држања две висине), студент мора решити следећи задатак. Претпостављамо да је БТ висина једнакокраке фигуре АБСД -а. Потребно је пронаћи сегменте АТ и ТД. Користећи горе описану формулу, неће бити тешко то учинити.
Хајде сада да схватимо како одредити радијусзаокружи користећи површину описаног трапеза. Спуштамо висину од врха Б до базе крвног притиска. Пошто је круг уписан у трапез, тада је БС + ПАКЛО = 2АБ или АБ = (БС + ПАКЛО) / 2. Из троугла АБН налазимо синα = БН / АБ = 2 * БН / (БС + ПАКАО). ПАБСД = (БС + ПАКАО) * БН / 2, БН = 2Р. Добијамо ПАБСД = (БС + ПАКЛО) * Р, следи да је Р = ПАБСД / (БС + ПАКАО).
.

Сада је време да пређемо на последњи елемент овог геометријског облика. Хајде да схватимо колико је средња линија трапеза (М) једнака:
1. Преко основа: М = (А + Б) / 2.
2. Кроз висину, базу и углове:
• М = А-Х * (цтгα + цтгβ) / 2;
• М = Б + Х * (цтгα + цтгβ) / 2.
3. Кроз висину, дијагонале и угао између њих. На пример, Д1 и Д2 су дијагонале трапеза; α, β - углови између њих:
М = Д1 * Д2 * синα / 2Х = Д1 * Д2 * синβ / 2Х.
4. Кроз површину и висину: М = П / Н.


























