
การศึกษากระบวนการที่เกิดขึ้นในเชิงสถิติระบบซับซ้อนด้วยขนาดอนุภาคขั้นต่ำและจำนวนมหาศาล แทบจะเป็นไปไม่ได้เลยที่จะพิจารณาแต่ละอนุภาคแยกกันดังนั้นจึงมีการแนะนำปริมาณทางสถิติ ได้แก่ ความเร็วเฉลี่ยของอนุภาคความเข้มข้นมวลของอนุภาค สูตรที่กำหนดลักษณะสถานะของระบบโดยคำนึงถึงพารามิเตอร์ด้วยกล้องจุลทรรศน์เรียกว่าสมการพื้นฐานของทฤษฎีจลน์โมเลกุลของก๊าซ (MKT)
การกำหนดความเร็วของการเคลื่อนที่ของอนุภาคเป็นครั้งแรกดำเนินการทดลอง การทดลองที่ทราบจากหลักสูตรของโรงเรียนซึ่งดำเนินการโดย Otto Stern ทำให้สามารถสร้างแนวคิดเกี่ยวกับความเร็วของอนุภาคได้ ในระหว่างการทดลองได้มีการตรวจสอบการเคลื่อนที่ของอะตอมเงินในกระบอกสูบที่หมุน: อันดับแรกอยู่ในสถานะหยุดนิ่งของการติดตั้งจากนั้นในระหว่างการหมุนด้วยความเร็วเชิงมุมที่แน่นอน
เป็นผลให้พบว่าความเร็วของโมเลกุลเงินเกินความเร็วของเสียงและคือ 500 ม. / วินาที ความจริงแล้วค่อนข้างน่าสนใจเนื่องจากเป็นเรื่องยากสำหรับบุคคลที่จะรู้สึกถึงความเร็วในการเคลื่อนที่ของอนุภาคในสสาร
ดูเหมือนจะเป็นไปได้ที่จะดำเนินการวิจัยต่อไปเฉพาะในระบบที่สามารถกำหนดพารามิเตอร์ได้โดยการวัดโดยตรงโดยใช้เครื่องมือทางกายภาพ ความเร็ววัดได้ด้วยมาตรวัดความเร็ว แต่แนวคิดในการติดมาตรวัดความเร็วเข้ากับอนุภาคเดียวนั้นไร้สาระ เฉพาะพารามิเตอร์ระดับมหภาคที่เกี่ยวข้องกับการเคลื่อนที่ของอนุภาคเท่านั้นที่สามารถวัดได้โดยตรง
ระบบใด ๆ ของร่างกายที่มีปฏิสัมพันธ์โดดเด่นด้วยพลังงานศักย์และพลังงานจลน์ของการเคลื่อนที่ ก๊าซจริงเป็นระบบที่ซับซ้อน ความแปรปรวนของพลังงานศักย์ไม่ได้ทำให้เกิดการจัดระบบ ปัญหาสามารถแก้ไขได้โดยการแนะนำแบบจำลองที่มีคุณสมบัติเฉพาะของก๊าซโดยปัดความซับซ้อนของปฏิสัมพันธ์ออกไป
ก๊าซในอุดมคติคือสถานะของสสารที่ปฏิสัมพันธ์ของอนุภาคมีค่าเล็กน้อยพลังงานศักย์ของปฏิสัมพันธ์มีแนวโน้มที่จะเป็นศูนย์ เฉพาะพลังงานของการเคลื่อนที่ซึ่งขึ้นอยู่กับความเร็วของอนุภาคเท่านั้นที่สามารถพิจารณาได้อย่างมีนัยสำคัญ

เปิดเผยความสัมพันธ์ระหว่างความดันและความเร็วของก๊าซการเคลื่อนที่ของอนุภาคทำให้สมการพื้นฐานของ MKT ของก๊าซในอุดมคติ อนุภาคที่เคลื่อนที่ในเรือเมื่อชนกับผนังจะถ่ายโอนไปยังแรงกระตุ้นซึ่งค่านี้สามารถกำหนดได้บนพื้นฐานของกฎข้อที่สองของนิวตัน:
การเปลี่ยนแปลงโมเมนตัมของอนุภาคในระหว่างการกระแทกแบบยืดหยุ่นนั้นเกี่ยวข้องกับการเปลี่ยนแปลงของส่วนประกอบแนวนอนของความเร็วของมัน F คือแรงที่กระทำจากอนุภาคบนผนังในช่วงเวลาสั้น ๆ t; ม0 คือมวลของอนุภาค
อนุภาคของก๊าซทั้งหมดเคลื่อนที่ไปในทิศทางของพื้นผิวด้วยความเร็ว v ชนกับพื้นผิวของพื้นที่ S ในช่วงเวลา ∆tกับ และอยู่ในกระบอกสูบปริมาตรSυกับΔt. ที่ความเข้มข้นของอนุภาค n ครึ่งหนึ่งของโมเลกุลจะเคลื่อนที่เข้าหาผนังและอีกครึ่งหนึ่งไปในทิศทางตรงกันข้าม
เมื่อพิจารณาการชนกันของอนุภาคทั้งหมดเราสามารถเขียนกฎของนิวตันสำหรับแรงที่กระทำบนไซต์:
เนื่องจากความดันก๊าซถูกกำหนดให้เป็นอัตราส่วนของแรงที่กระทำในแนวตั้งฉากกับพื้นผิวต่อพื้นที่ส่วนหลังเราจึงสามารถเขียน:
ความสัมพันธ์ที่เป็นผลลัพธ์เป็นสมการพื้นฐานของ MKT ไม่สามารถอธิบายระบบทั้งหมดได้เนื่องจากพิจารณาเฉพาะการเคลื่อนที่ในทิศทางเดียว
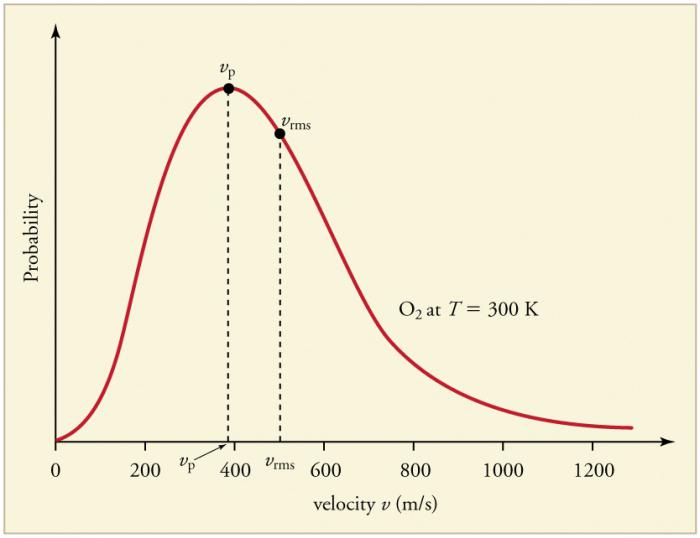
การชนกันของอนุภาคก๊าซบ่อยๆอย่างต่อเนื่องกับผนังและกันและกันนำไปสู่การสร้างการกระจายทางสถิติของอนุภาคที่มีความเร็ว (พลังงาน) ทิศทางของเวกเตอร์ความเร็วทั้งหมดมีความเป็นไปได้เท่ากัน การกระจายนี้เรียกว่าการแจกแจงแบบแม็กซ์เวลล์ ในปีพ. ศ. 2403 รูปแบบนี้ถูกอนุมานโดย J. Maxwell บนพื้นฐานของ MKT พารามิเตอร์หลักของกฎการกระจายเรียกว่าความเร็ว: น่าจะเป็นที่สอดคล้องกับค่าสูงสุดของเส้นโค้งและ rms vตร.ม. = √ ‹v2› - กำลังสองเฉลี่ยของความเร็วอนุภาค
การเพิ่มขึ้นของอุณหภูมิของก๊าซสอดคล้องกับการเพิ่มขึ้นของค่าความเร็ว
จากข้อเท็จจริงที่ว่าความเร็วทั้งหมดเท่ากันและโมดูลมีค่าเท่ากันเราสามารถพิจารณา:
สมการพื้นฐานของ MKT โดยคำนึงถึงค่าเฉลี่ยของความดันก๊าซมีรูปแบบ:
อัตราส่วนนี้มีความพิเศษตรงที่กำหนดความสัมพันธ์ระหว่างพารามิเตอร์ของกล้องจุลทรรศน์: ความเร็วมวลอนุภาคความเข้มข้นของอนุภาคและความดันก๊าซโดยทั่วไป
โดยใช้แนวคิดเรื่องพลังงานจลน์ของอนุภาคสมการพื้นฐานของ MKT สามารถเขียนใหม่ได้แตกต่างกัน:
ความดันก๊าซเป็นสัดส่วนกับพลังงานจลน์เฉลี่ยของอนุภาค
เป็นที่น่าสนใจสำหรับปริมาณก๊าซคงที่ภาชนะปิดคุณสามารถเชื่อมโยงความดันของก๊าซและค่าเฉลี่ยของพลังงานของการเคลื่อนที่ของอนุภาค ในกรณีนี้สามารถวัดความดันได้โดยการวัดพลังงานของอนุภาค
ต้องดำเนินการอย่างไร? ปริมาณใดบ้างที่สามารถเปรียบเทียบกับพลังงานจลน์? ค่านี้กลายเป็นอุณหภูมิ


น่าสนใจมากขึ้นจากมุมมองของความเป็นอิสระจากคุณสมบัติของของเหลวที่ใช้งานได้ถือได้ว่าเป็นเครื่องวัดอุณหภูมิก๊าซ มาตราส่วนของพวกเขาไม่ขึ้นอยู่กับประเภทของก๊าซที่ใช้ ในอุปกรณ์ดังกล่าวเราสามารถเลือกอุณหภูมิที่ความดันก๊าซมีแนวโน้มเป็นศูนย์ได้โดยสมมุติฐาน การคำนวณแสดงว่าค่านี้สอดคล้องกับ -273.15 เกี่ยวกับจาก.มาตราส่วนอุณหภูมิ (มาตราส่วนอุณหภูมิสัมบูรณ์หรือมาตราส่วนเคลวิน) ถูกนำมาใช้ในปีพ. ศ. 2391 อุณหภูมิที่เป็นไปได้ของความดันก๊าซเป็นศูนย์ถูกนำมาเป็นจุดหลักของมาตราส่วนนี้ ส่วนหน่วยของมาตราส่วนเท่ากับค่าหน่วยของมาตราส่วนเซลเซียส สะดวกกว่าในการเขียนสมการพื้นฐานของ MKT โดยใช้อุณหภูมิในการศึกษากระบวนการของก๊าซ
ในเชิงประจักษ์คุณสามารถตรวจสอบให้แน่ใจว่าความดันก๊าซเป็นสัดส่วนกับอุณหภูมิ ในเวลาเดียวกันพบว่าความดันแปรผันโดยตรงกับความเข้มข้นของอนุภาค:
โดยที่Т - อุณหภูมิสัมบูรณ์ค่าคงที่ k เท่ากับ 1.38 • 10-23เจ / เค
ปริมาณพื้นฐานซึ่งมีค่าคงที่สำหรับก๊าซทั้งหมดเรียกว่าค่าคงที่ Boltzmann
เมื่อเปรียบเทียบการพึ่งพาความดันต่ออุณหภูมิและสมการพื้นฐานของก๊าซ MKT เราสามารถเขียนได้:
ค่าเฉลี่ยของพลังงานจลน์ของการเคลื่อนที่ของโมเลกุลของแก๊สเป็นสัดส่วนกับอุณหภูมิ นั่นคืออุณหภูมิสามารถใช้เป็นตัววัดพลังงานจลน์ของการเคลื่อนที่ของอนุภาค


























