
Термодинаміка як самостійний розділфізичної науки виникла в першій половині XIX століття. Гримнув століття машин. Промислова революція вимагала вивчити і осмислити процеси, пов'язані з функціонуванням теплових двигунів. На зорі машинної ери винахідники-одинаки могли собі дозволити використовувати лише інтуїцію і «метод тику». Не було соціального замовлення на відкриття та винаходи, нікому навіть в голову не могло прийти, що вони можуть бути корисні. Але коли теплові (а трохи пізніше і електричні) машини стали основою виробництва, ситуація змінилася. Вчені нарешті поступово розібралися з термінологічної плутаниною, що панувала до середини XIX століття, визначившись, що називати енергією, що силою, що - імпульсом.
Почнемо з загальновідомих відомостей.Класична термодинаміка заснована на кількох постулатах (засадах), послідовно вводилися протягом XIX століття. Тобто ці положення не є доказовим в її рамках. Вони були сформульовані в результаті узагальнення емпіричних даних.
Перший закон - це додаток закону збереженняенергії до опису поведінки макроскопічних систем (що складаються з великої кількості частинок). Коротко його можна сформулювати так: запас внутрішньої енергії ізольованої термодинамічної системи завжди залишається постійним.
Сенс другого закону термодинаміки полягає у визначенні напрямку, в якому протікають процеси в таких системах.
Третій закон дозволяє точно визначити таку величину, як ентропія. Розглянемо її докладніше.
Формулювання другого закону термодинаміки булазапропонована в 1850 році Рудольфом Клаузиусом: «Неможливий мимовільний перехід теплоти від менш нагрітого тіла до більш нагрітого». При цьому Клаузиус підкреслював заслугу Саді Карно, ще в 1824 році встановив, що частка енергії, яка може бути перетворена в роботу теплової машини, залежить тільки від різниці температур нагрівача і холодильника.

При подальшій розробці другого початкутермодинаміки Клаузіус вводить поняття ентропії - міри кількості енергії, яка незворотньо переходить в форму, непридатну для звернення в роботу. Клаузиус висловив цю величину формулою dS = dQ / T, де dS, що визначає зміна ентропії. тут:
dQ - зміна теплоти;
T - абсолютна температура (та сама, яка вимірюється в кельвінах).
Простий приклад:помацайте капот вашого автомобіля при включеному двигуні. Він явно тепліше навколишнього середовища. Але ж двигун автомобіля призначений не для того, щоб нагрівати капот або воду в радіаторі. Перетворюючи хімічну енергію бензину в теплову, а потім в механічну, він робить корисну роботу - обертає вал. Але велика частина виробленого тепла втрачається, так як ніякої корисної роботи з нього витягти не можна, а то, що вилітає з вихлопної труби, вже жодним чином бензином не є. При цьому теплова енергія втрачається, але не зникає, а розсіюється (диссипирует). Гарячий капот, звичайно, остигає, а кожен цикл циліндрів в двигуні знову додає йому теплоту. Таким чином система прагне досягти термодинамічної рівноваги.
Клаузиус вивів загальний принцип для другого початкутермодинаміки у формулі dS ≥ 0. Фізичний сенс її можна визначити, як "неубиванія" ентропії: в оборотних процесах вона не змінюється, в необоротних - зростає.
Слід зауважити, що всі реальні процесинезворотні. Термін «неубиванія» відображає лише той факт, що в розгляд явища включений також теоретично можливий ідеалізований варіант. Тобто кількість недоступною енергії в будь-якому мимовільному процесі збільшується.
Макс Планк вніс серйозний вклад в розробкутермодинаміки. Крім роботи над статистичної інтерпретацією другого початку, він взяв діяльну участь в постулювало третього початку термодинаміки. Перша формулювання належить Вальтеру Нернст і відноситься до 1906 року. Теорема Нернста розглядає поведінку рівноважної системи при температурі, яка прагне до абсолютного нуля. Перше і друге початку термодинаміки не дають можливості з'ясувати, якою буде ентропія в даних умовах.

При T = 0 K енергія дорівнює нулю, частки системиприпиняють хаотичні теплові руху і утворюють впорядковану структуру, кристал з термодинамічної ймовірністю, яка дорівнює одиниці. Значить, ентропія теж наближається до нуля (нижче ми дізнаємося, чому так відбувається). У реальності вона навіть робить це дещо раніше, з чого випливає, що охолодження будь-термодинамічної системи, будь-якого тіла до абсолютного нуля неможливо. Температура буде як завгодно наближатися до цієї точки, але не досягне її.
Клаузиус узагальнив і сформулював перше і друге початку термодинаміки таким чином: повна енергія будь-якої замкнутої системи завжди залишається постійною, а повна ентропія зростає з плином часу.
Перша частина цього твердження накладає заборону навічний двигун першого роду - пристрій, що робить роботу без припливу енергії із зовнішнього джерела. Друга частина забороняє і вічний двигун другого роду. Така машина переводила б енергію системи в роботу без ентропійному компенсації, не порушуючи закону збереження. Можна було б відкачувати тепло з рівноважної системи, наприклад, смажити яєчню або лити сталь за рахунок енергії теплового руху молекул води, охолоджуючи її при цьому.
Друге і третє початку термодинаміки забороняють вічний двигун другого роду.
На жаль, у природи нічого не можна отримати не тільки даром, доводиться ще й комісію виплачувати.

Мало знайдеться в науці понять, які викликалистільки неоднозначних емоцій не тільки у широкої публіки, а й в середовищі самих вчених, скільки довелося на частку ентропії. Фізики, і в першу чергу сам Клаузиус, практично відразу екстраполювали закон неубиванія спочатку на Землю, а потім і на весь Всесвіт (чому б і ні, адже її теж можна вважати термодинамічної системою). В результаті фізична величина, важливий елемент розрахунків у багатьох технічних додатках, стала сприйматися як втілення якогось вселенського Зла, що знищує світлий і добрий світ.
У середовищі вчених є і такі думки:оскільки, відповідно до другого початку термодинаміки, ентропія необоротно зростає, рано чи пізно вся енергія Всесвіту деградує в розсіяну форму, і настане «теплова смерть». Чому тут радіти? Клаузіус, наприклад, кілька років не вирішувалося на публікацію своїх висновків. Зрозуміло, гіпотеза «теплової смерті» негайно викликала безліч заперечень. Серйозні сумніви в її правильності є і зараз.
У 1867 році Джеймс Максвелл, один з авторівмолекулярно-кінетичної теорії газів, в дуже наочному (хоч і вигаданому) експерименті продемонстрував гадану парадоксальність другого закону термодинаміки. Коротко досвід можна викласти наступним чином.
Нехай є посудину з газом.Молекули в ньому рухаються хаотично, швидкості їх не однакові, але середня кінетична енергія однакова по всьому судині. Тепер розділимо посудину перегородкою на дві ізольовані частини. Середня швидкість молекул в обох половинках судини залишиться однаковою. Перегородку сторожить крихітний демон, який дозволяє більш швидким, «гарячим» молекулам проникати в одну частину, а більш повільним «холодним» - в іншу. В результаті в першій половинці газ нагріється, в другій - охолоне, тобто зі стану термодинамічної рівноваги система перейде до різниці температурних потенціалів, що означає зменшення ентропії.
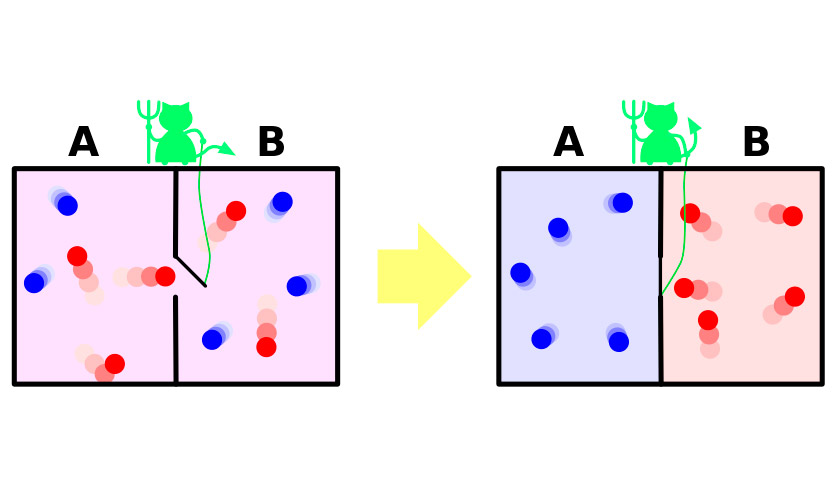
Вся проблема в тому, що в експерименті системаздійснює цей перехід не мимовільно. Вона отримує ззовні енергію, за рахунок якої відкривається і закривається перегородка, або система з необхідністю включає в себе демона, що витрачається свою енергію на виконання обов'язків воротаря. Збільшення ентропії демона з надлишком покриє зменшення її в газі.
Візьмемо склянку з водою і залишимо його на столі.Спостерігати за склянкою не обов'язково, досить через деякий час повернутися і перевірити стан води в ньому. Ми побачимо, що її кількість зменшилася. Якщо ж залишити стакан надовго, в ньому взагалі не виявиться води, так як вся вона випарується. На самому початку процесу всі молекули води знаходилися в деякій обмеженою стінками склянки області простору. В кінці експерименту вони розлетілися по всій кімнаті. В обсязі кімнати у молекул набагато більше можливостей змінювати своє місце розташування без всяких наслідків для стану системи. Ми ніяк не зможемо зібрати їх в спаяний "колектив" і загнати назад в стакан, щоб з користю для здоров'я випити воду.

Це означає, що система еволюціонувала достаном з більш високою ентропією. Виходячи з другого закону термодинаміки, ентропія, або процес розсіювання частинок системи (в даному випадку молекул води) незворотній. Чому це так?
Клаузіус не відповів на це питання, та й ніхто інший не зміг цього зробити до Людвіга Больцмана.
У 1872 році цей учений ввів в наукустатистичне тлумачення другого закону термодинаміки. Адже макроскопічні системи, з якими має справу термодинаміка, утворені великою кількістю елементів, поведінка яких підпорядковується статистичним законам.
Повернемося до молекул води.Хаотично літаючи по кімнаті, вони можуть займати різні положення, мати деякі відмінності в швидкостях (молекули постійно стикаються один з одним і з іншими частинками в повітрі). Кожен варіант стану системи молекул називається микростанів, і таких варіантів безліч. При реалізації переважної більшості варіантів макросостояніе системи не зміниться ніяк.
Знамените співвідношення S = k lnW пов'язує числоможливих способів, яким можна виразити певне макросостояніе термодинамічної системи (W), з її ентропією S. Величину W називають термодинамічної ймовірністю. Остаточний вигляд цієї формули надав Макс Планк. Коефіцієнт k - надзвичайно малу величину (1,38 × 10-23 Дж / К), що характеризує зв'язок між енергією і температурою, Планк назвав постійної Больцмана в честь вченого, який першим запропонував статистичне тлумачення другого закону термодинаміки.

Ясно, що W - завжди натуральне число 1, 2, 3, ... N(Не буває дрібного кількості способів). Тоді логарифм W, а отже, і ентропія, не можуть бути негативними. При єдино можливий для системи микростанів ентропія стає рівною нулю. Якщо повернутися до нашого склянці, цей постулат можна змалювати таку картину: молекули води, безладно снують по кімнаті, повернулися назад в стакан. При цьому кожна в точності повторила свій шлях і зайняла в склянці те саме місце, в якому перебувала перед вильотом. Ніщо не забороняє реалізацію цього варіанту, при якому ентропія дорівнює нулю. Тільки чекати здійснення такої зникаюче малу ймовірність не варто. Це один із прикладів того, що можна здійснити лише теоретично.
Отже, молекули хаотично літають по кімнатірізними способами. Немає ніякої закономірності в їх розташуванні, немає порядку в системі, як не міняй варіанти микросостояний, не простежується жодної виразної структури. У склянці було те ж саме, але через обмеженість простору молекули міняли своє положення не так активно.
Хаотичний, невпорядковане стан системияк найбільш ймовірне відповідає її максимальної ентропії. Вода в склянці являє приклад більш нізкоентропійного стану. Перехід до нього з рівномірно розподіленого по кімнаті хаосу практично неможливий.
Наведемо більш зрозумілий для всіх нас приклад -прибирання безладу в будинку. Щоб все розставити по місцях, нам теж доводиться витрачати енергію. У процесі цієї роботи нам стає жарко (тобто ми не мерзнемо). Виявляється, ентропія може принести користь. Це так і є. Можна сказати навіть більше: ентропія, а через неї другий початок термодинаміки (поряд з енергією) керують Всесвіту. Погляньмо ще раз на зворотні процеси. Так виглядав би світ, якби не було ентропії: ніякого розвитку, ніяких галактик, зірок, планет. Ніякого життя ...

Ще трохи інформації про «теплової смерті».Є хороші новини. Оскільки, відповідно до статистичної теорії, «заборонені» процеси насправді є малоймовірними, в термодинамічно рівноважної системі виникають флуктуації - спонтанні порушення другого закону термодинаміки. Вони можуть бути як завгодно великими. При включенні гравітації в термодинамічну систему розподіл часток вже не буде хаотично-рівномірним, а стан максимальної ентропії не буде досягнуто. Крім того, Всесвіт не є незмінною, постійною, стаціонарної. Отже, сама постановка питання про «теплової смерті» позбавлена сенсу.


























