
Nun werden wir über geometrische Optik sprechen.In diesem Abschnitt wird viel Zeit für ein Objekt wie eine Linse aufgewendet. Es kann ja auch anders sein. Gleichzeitig ist die Formel einer dünnen Linse in allen Fällen gleich. Sie müssen nur wissen, wie Sie es richtig anwenden.

Es ist immer ein für Lichtstrahlen transparenter Körper, der eine besondere Form hat. Das Erscheinungsbild des Objekts wird von zwei sphärischen Flächen bestimmt. Einer von ihnen kann durch einen flachen ersetzt werden.
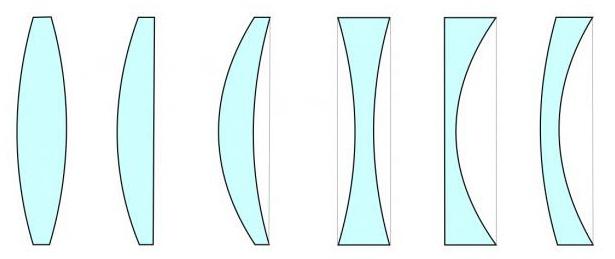
Причем у линзы может оказаться толще середина или die Kanten. Im ersten Fall heißt es konvex, im zweiten konkav. Je nachdem, wie konkave, konvexe und flache Oberflächen kombiniert werden, können die Linsen auch unterschiedlich sein. Nämlich: bikonvex und bikonkav, plankonvex und plankonkav, konvexkonkav und konkavkonvex.
Unter normalen Bedingungen werden diese Objekte in verwendetin der luft. Sie bestehen aus einer Substanz, deren optische Dichte größer ist als die von Luft. Daher sammelt sich eine konvexe Linse und eine konkave Linse streut.
Bevor ich über dünne Linse Formelmüssen Sie sich für die Grundkonzepte entscheiden. Sie müssen bekannt sein. Da sie ständig von verschiedenen Aufgaben angesprochen werden.
Haupt optische Achse - eine gerade Linie.Es wird durch die Mitten beider sphärischer Flächen gezogen und bestimmt die Position der Linsenmitte. Darüber hinaus gibt es zusätzliche optische Achse. Sie werden durch einen Punkt gezogen, der das Zentrum der Linse ist, enthalten jedoch nicht die Zentren der sphärischen Oberflächen.
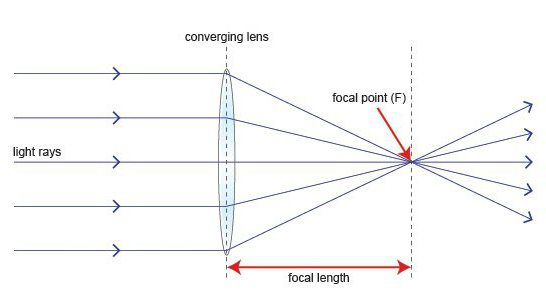
In der Formel einer dünnen Linse gibt es eine Größe, die ihre Brennweite bestimmt. Der Fokus ist also ein Punkt auf der optischen Hauptachse. Darin kreuzen sich Strahlen, die sich parallel zur angegebenen Achse kreuzen.
Und Tricks jeweils dünne Linse sind immer zwei. Sie sind auf beiden Seiten seiner Oberflächen angeordnet. Beide Fokusse auf den Sammler sind gültig. In Streuung - imaginär.
Die Entfernung vom Objektiv zum Brennpunkt ist die Brennweite (Buchstabe F). Außerdem kann sein Wert positiv (beim Sammeln) oder negativ (beim Streuen) sein.
Ein weiteres Merkmal ist die Brennweite - die optische Leistung. Es ist üblich zu bezeichnen D. Sein Wert ist immer der Kehrwert des Fokus, d.h. D = 1 /F. Gemessene optische Leistung in Dioptrien (abgekürzte Dioptrien).
Zusätzlich zu der bereits festgelegten Brennweite müssen Sie verschiedene Abstände und Größen kennen. Sie sind für alle Objektivtypen gleich und in der Tabelle aufgeführt.
| Notation | Titel |
| d | Objektabstand |
| x | Höhe des Studienfachs |
| f | Abstand zum Bild |
| X | Höhe des resultierenden Bildes |
Alle angegebenen Abstände und Höhen werden üblicherweise in Metern gemessen.
In der Physik wird der Begriff der Vergrößerung auch mit der Formel einer dünnen Linse in Verbindung gebracht. Es ist definiert als das Verhältnis der Größe des Bildes zur Höhe des Subjekts, d. H. H / h. Es kann mit dem Buchstaben G bezeichnet werden.
Sie müssen dies wissen, um die Formel zu erhaltendünne Linse, Sammeln oder Streuen. Die Zeichnung beginnt damit, dass beide Objektive ein eigenes schematisches Bild haben. Beide sehen aus wie ein Schnitt. Nur im Sammeln an seinen Enden sind die Pfeile nach außen gerichtet, und in der Streuung nach innen von diesem Segment.
Nun muss auf dieses Segment gezeichnet werdensenkrecht zu seiner Mitte. Dies zeigt die optische Hauptachse. Darauf, auf beiden Seiten des Objektivs im gleichen Abstand, soll es Tricks notieren.
Das Objekt, dessen Bild Sie erstellen möchten, wird in Form eines Pfeils gezeichnet. Es zeigt an, wo sich die Oberseite des Elements befindet. In der Regel wird ein Objekt parallel zur Linse platziert.
Um ein Bild von einem Objekt zu erstellen,Finden Sie einfach die Punkte an den Enden des Bildes und verbinden Sie sie. Jeder dieser beiden Punkte kann aus dem Schnittpunkt zweier Strahlen resultieren. Am einfachsten zu bauen sind zwei davon.
Vom angegebenen Punkt kommend parallel zur Hauptleitungoptische Achse. Nach dem Kontakt mit der Linse geht er durch den Hauptfokus. Wenn es sich um eine Sammellinse handelt, befindet sich dieser Fokus hinter der Linse und der Strahl geht durch sie hindurch. Wenn Streuung berücksichtigt wird, muss der Strahl so gezeichnet werden, dass seine Fortsetzung durch den Fokus vor der Linse verläuft.
Gehen Sie direkt durch das optische Zentrum des Objektivs. Er ändert seine Richtung nicht nach ihr.
Es gibt Situationen, in denen ein Artikel geliefert wirdsenkrecht zur optischen Hauptachse und endet auf dieser. Dann genügt es, ein Bild von einem Punkt zu erstellen, der der Kante des Pfeils entspricht und nicht auf der Achse liegt. Und dann zeichnen Sie daraus eine Senkrechte zur Achse. Dies wird das Bild des Subjekts sein.
Der Schnittpunkt der konstruierten Punkte ergibt ein Bild.In einer dünnen Sammellinse wird ein reales Bild erhalten. Das heißt, es wird direkt am Schnittpunkt der Strahlen erhalten. Eine Ausnahme ist die Situation, in der sich das Motiv (wie bei einer Lupe) zwischen Objektiv und Fokus befindet und sich das Bild als imaginär herausstellt. In der Streuung erweist es sich immer als imaginär. Schließlich wird es am Schnittpunkt nicht der Strahlen selbst, sondern ihrer Ausdehnungen erhalten.
Das eigentliche Bild wird normalerweise mit einer durchgezogenen Linie gezeichnet. Aber die imaginäre - gepunktete Linie. Dies liegt daran, dass der erste tatsächlich dort vorhanden ist und der zweite nur zu sehen ist.
Dies geschieht zweckmäßigerweise anhand einer Zeichnung, die den Aufbau eines realen Bildes in einer Sammellinse veranschaulicht. Die Bezeichnung der Segmente ist auf der Zeichnung angegeben.
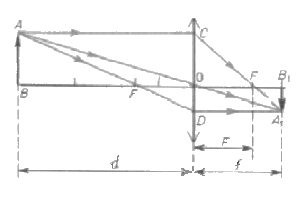
Der Optikbereich wird nicht umsonst als geometrisch bezeichnet. Es werden Kenntnisse aus diesem Bereich der Mathematik benötigt. Zuerst müssen Sie die Dreiecke AOW und A betrachten1OV1. Sie sind ähnlich, weil sie zwei gleiche Winkel haben (gerade und vertikal). Aus ihrer Ähnlichkeit folgt, dass die Module der Segmente A1In der1 und AB bezeichnen als Module der Segmente von OB1 und OB.
Ähnlich (basierend auf demselben Prinzip in zwei Winkeln) sind zwei weitere Dreiecke: COF und A1Fb1. In ihnen bestehen gleiche Beziehungen bereits aus solchen Modulen von Segmenten: A1In der1 mit CO und Fb1mit dem OF. Aufgrund der Konstruktion sind die Segmente AB und CO gleich. Daher sind die linken Seiten der angegebenen Gleichheitsbeziehungen gleich. Daher sind die richtigen gleich. Das heißt, OB1 / S ist gleich Fb1/ OF.
In der angegebenen Gleichheit können die durch Punkte angegebenen Segmente durch die entsprechenden physikalischen Konzepte ersetzt werden. So ov1 Ist der Abstand vom Objektiv zum Bild. OB ist der Abstand vom Motiv zum Objektiv. OF - Brennweite. Ein Segment Fb1 gleich dem Unterschied in der Entfernung zum Bild und Fokus. Daher kann es auf andere Weise umgeschrieben werden:
f / d = (f - F) / F oder Ff = df - dF.
Um die Formel für dünne Linsen abzuleiten, muss die letzte Gleichheit in geteilt werden dfF. Dann stellt sich heraus:
1 / d + 1 / f = 1 / F.
Dieser hat die Formel einer dünnen Sammellinse.Eine streuende Brennweite ist negativ. Dies führt zu einer Änderung der Gleichstellung. Es stimmt, es ist unbedeutend. Gerade in der Formel einer dünnen Streulinse gibt es ein Minus vor dem Verhältnis 1 /F. Also:
1 / d + 1 / f = - 1 / F.
Zustand Die Brennweite der Sammellinse beträgt 0,26 m. Die Vergrößerung muss berechnet werden, wenn sich das Motiv in einer Entfernung von 30 cm befindet.
Lösung. Es beginnt mit der Einführung der Notation und der Übersetzung von Einheiten in C. Bekannt d = 30 cm = 0,3 m und F = 0,26 M. Nun müssen Sie die Formel auswählen, die für die Vergrößerung als Hauptformel angegeben ist, die zweite - für eine dünne Sammellinse.
Sie müssen irgendwie kombiniert werden. Dazu müssen Sie die Zeichnung der Bildkonstruktion in der Sammellinse berücksichtigen. Aus diesen Dreiecken ist klar, dass Γ = H / h= f / d. Das heißt, um die Vergrößerung zu finden, müssen Sie das Verhältnis der Entfernung zum Bild zur Entfernung zum Motiv berechnen.
Der zweite ist bekannt. Die Entfernung zum Bild soll sich jedoch aus der oben angegebenen Formel ergeben. Es stellt sich heraus, dass
f = df / (d - F).
Nun müssen diese beiden Formeln kombiniert werden.
R = df / (d(d - F)) = F / (d - F).
An diesem Punkt kommt es zur Lösung des Problems der Dünnlinsenformel auf elementare Berechnungen an. Es bleiben die bekannten Mengen zu ersetzen:
G = 0,26 / (0,3 - 0,26) = 0,26 / 0,04 = 6,5.
Antwort: Das Objektiv bietet eine 6,5-fache Vergrößerung.

Zustand Die Lampe befindet sich einen Meter von der Sammellinse entfernt. Ein Bild der Spirale wird auf einem 25 cm vom Objektiv entfernten Bildschirm aufgenommen. Berechnen Sie die Brennweite des angegebenen Objektivs.
Die Entscheidung Folgende Werte sollen in die Daten geschrieben werden: d = 1 m und f = 25 cm = 0,25 m Diese Information reicht aus, um die Brennweite aus der Formel einer dünnen Linse zu berechnen.
Also 1 /F = 1/1 + 1 / 0,25 = 1 + 4 = 5. Bei dem Problem ist es jedoch erforderlich, den Fokus und nicht die optische Leistung zu kennen. Daher bleibt es nur, 1 durch 5 zu teilen und die Brennweite zu erhalten:
F = 1/5 = 0,2 m
Antwort: Die Brennweite der Sammellinse beträgt 0,2 m.
Zustand. Die Kerze wurde in einem Abstand von 15 cm von der Sammellinse platziert. Seine optische Leistung beträgt 10 Dioptrien. Der Bildschirm hinter der Linse ist so eingestellt, dass ein klares Bild der Kerze entsteht. Was ist dieser Abstand gleich?
Die Entscheidung In einem kurzen Datensatz sollen folgende Daten geschrieben werden: d = 15 cm = 0,15 m, D = 10 Dioptrien Die obige Formel sollte mit einer kleinen Änderung geschrieben werden. Nämlich auf die rechte Seite der Gleichheit setzen D statt 1 /F.
Nach mehreren Transformationen erhalten wir die folgende Formel für den Abstand von der Linse zum Bild:
f = d / (dd - 1).
Jetzt müssen Sie alle Zahlen ersetzen und zählen. Es stellt sich heraus, dass dieser Wert für f: 0,3 m.
Antwort: Der Abstand zwischen Objektiv und Bildschirm beträgt 0,3 m.

Zustand Das Objekt und sein Bild sind 11 cm voneinander entfernt. Eine Sammellinse ergibt eine 3-fache Vergrößerung. Finde ihre Brennweite.
Die Entscheidung Der Abstand zwischen dem Objekt und seinem Bild wird zweckmäßigerweise durch den Buchstaben angegeben L = 72 cm = 0,72 m, G = 3 erhöhen.
Hier sind zwei Situationen möglich.Erstens - das Motiv befindet sich hinter dem Fokus, das heißt, das Bild ist real. In der zweiten befindet sich ein Objekt zwischen dem Fokus und der Linse. Dann befindet sich das Bild auf derselben Seite wie das Motiv und ist imaginär.
Betrachten Sie die erste Situation. Das Motiv und das Bild befinden sich auf gegenüberliegenden Seiten der Sammellinse. Hier können Sie die folgende Formel schreiben: L = d + f. Die zweite Gleichung soll schreiben: G = f / d. Es ist notwendig, das System dieser Gleichungen mit zwei Unbekannten zu lösen. Dazu ersetzen L um 0,72 m und Г um 3.
Aus der zweiten Gleichung geht hervor, dass f = 3d. Dann wird der erste wie folgt konvertiert: 0,72 = 4d. Einfach zu zählen d = 0,18 (m). Jetzt leicht zu erkennen f = 0,54 (m).
Es bleibt die Formel für dünne Linsen zur Berechnung der Brennweite zu verwenden. F = (0,18 × 0,54) / (0,18 + 0,54) = 0,135 (m). Dies ist die Antwort für den ersten Fall.
In der zweiten Situation ist das Bild imaginär und die Formel für L wird anders sein: L = f - d. Die zweite Gleichung für das System ist dieselbe. In gleicher Weise argumentieren wir d = 0,36 (m) und f = 1,08 (m). Eine ähnliche Berechnung der Brennweite ergibt folgendes Ergebnis: 0,54 (m).
Antwort: Die Brennweite des Objektivs beträgt 0,135 m oder 0,54 m.
Der Strahlengang in einer dünnen Linse ist wichtigpraktische Anwendung der geometrischen Optik. Schließlich werden sie in vielen Geräten eingesetzt, von einfachen Lupen bis hin zu Präzisionsmikroskopen und Teleskopen. Daher müssen Sie über sie Bescheid wissen.
Die abgeleitete Formel einer dünnen Linse ermöglicht das Lösenviele aufgaben. Darüber hinaus können Sie Rückschlüsse darauf ziehen, welche Bilder unterschiedliche Arten von Linsen ergeben. In diesem Fall ist es ausreichend, die Brennweite und die Entfernung zum Motiv zu kennen.


























