
Ahora hablaremos de óptica geométrica.En esta sección, se dedica mucho tiempo a un objeto como una lente. Después de todo, puede ser diferente. Al mismo tiempo, la fórmula de una lente delgada es la misma para todos los casos. Solo necesita saber cómo aplicarlo correctamente.

Siempre es un cuerpo transparente a los rayos de luz, que tiene una forma especial. La apariencia del objeto está dictada por dos superficies esféricas. Uno de ellos puede ser reemplazado por uno plano.
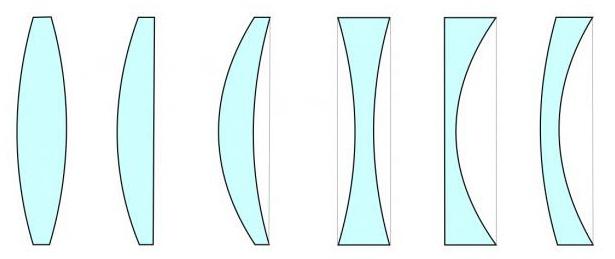
Además, la lente puede ser más gruesa en el medio olos bordes En el primer caso, se llamará convexo, en el segundo - cóncavo. Además, dependiendo de cómo se combinen las superficies cóncavas, convexas y planas, las lentes también pueden ser diferentes. A saber: biconvexo y biconcavo, plano-convexo y plano-cóncavo, convexo-cóncavo y cóncavo-convexo.
En condiciones normales, estos objetos se utilizan enen el aire Están hechos de una sustancia cuya densidad óptica es mayor que la del aire. Por lo tanto, se acumulará una lente convexa y se dispersará una lente cóncava.
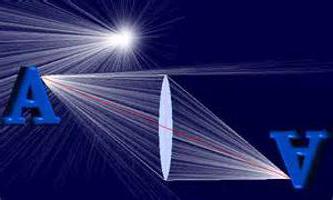
Antes de hablar de fórmula de lente delgada, debes decidir sobre los conceptos básicos. Deben ser conocidos. Ya que serán abordados constantemente por diversas tareas.
El eje óptico principal es recto.Se dibuja a través de los centros de ambas superficies esféricas y determina la ubicación del centro de la lente. Hay ejes ópticos adicionales. Se dibujan a través de un punto que es el centro de la lente, pero no contienen los centros de las superficies esféricas.
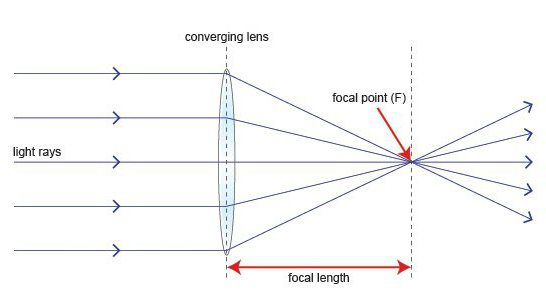
En la fórmula de una lente delgada hay una cantidad que determina su distancia focal. Entonces, el foco es un punto en el eje óptico principal. En él, los rayos que cruzan paralelos al eje especificado se cruzan.
Además, siempre hay dos trucos para cada lente delgada. Están ubicados a ambos lados de sus superficies. Ambos enfoques en el coleccionista son válidos. En dispersión - imaginario.
La distancia desde la lente al punto focal es la distancia focal (letra F). Además, su valor puede ser positivo (en el caso de la recolección) o negativo (para la dispersión).
Otra característica está asociada con la distancia focal: la potencia óptica. Es costumbre denotar D. Su valor es siempre el recíproco del foco, es decir. D = 1 /F. Potencia óptica medida en dioptrías (dioptrías abreviadas).
Además de la distancia focal ya especificada, necesitará conocer varias distancias y tamaños. Para todos los tipos de lentes son iguales y se presentan en la tabla.
| Notación | Título |
| d | distancia al sujeto |
| x | altura de la asignatura estudiada |
| f | distancia a la imagen |
| X | altura de la imagen resultante |
Todas las distancias y alturas indicadas generalmente se miden en metros.
En física, la noción de aumento también se asocia con la fórmula de una lente delgada. Se define como la relación entre el tamaño de la imagen y la altura del sujeto, es decir, H / h.. Se puede denotar con la letra G.
Necesitas saber esto para obtener la fórmulaLente delgada, recogida o dispersión. El dibujo comienza con el hecho de que ambas lentes tienen su propia imagen esquemática. Ambos parecen un corte. Solo en la recolección en sus extremos las flechas se dirigen hacia afuera, y en la dispersión - hacia adentro de este segmento.
Ahora es necesario dibujar a este segmentoperpendicular a su medio. Esto mostrará el eje óptico principal. En él, a ambos lados de la lente a la misma distancia, se supone que debe notar trucos.
El objeto cuya imagen desea construir se dibuja en forma de flecha. Muestra dónde está la parte superior del artículo. En general, un objeto se coloca paralelo a la lente.
Para construir una imagen de un objeto,solo encuentre los puntos de los extremos de la imagen y luego conéctelos. Cada uno de estos dos puntos puede resultar de la intersección de dos rayos. Los más simples de construir son dos de ellos.
Идущий из указанной точки параллельно главной eje óptico Después del contacto con la lente, pasa por el foco principal. Si estamos hablando de una lente colectora, entonces este foco está detrás de la lente y el rayo lo atraviesa. Cuando se considera la dispersión, el haz debe dibujarse de modo que su continuación pase a través del foco frente a la lente.
Pasando directamente por el centro óptico de la lente. Él no cambia su dirección después de ella.
Hay situaciones en las que se entrega un artículo.perpendicular al eje óptico principal y termina en él. Entonces es suficiente para construir una imagen de un punto que corresponde al borde de la flecha, no acostado en el eje. Y luego dibuje de ella una perpendicular al eje. Esta será la imagen del sujeto.
La intersección de los puntos construidos da una imagen.En una lente colectora delgada, se obtiene una imagen real. Es decir, se obtiene directamente en la intersección de los rayos. Una excepción es la situación cuando el sujeto se coloca entre la lente y el foco (como en una lupa), luego la imagen resulta ser imaginaria. En la dispersión, siempre resulta ser imaginario. Después de todo, se obtiene en la intersección no de los rayos en sí, sino de sus extensiones.
La imagen real generalmente se dibuja con una línea continua. Pero el imaginario - línea punteada. Esto se debe al hecho de que el primero está realmente presente allí, y el segundo solo se ve.
Esto se realiza convenientemente sobre la base de un dibujo que ilustra la construcción de una imagen real en una lente colectora. La designación de los segmentos se indica en el dibujo.
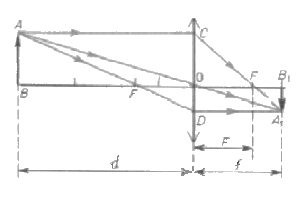
La sección de óptica no es en vano llamada geométrica. Tomará conocimiento de esta sección de matemáticas. Primero debes considerar los triángulos AOW y A1OV1. Son similares, porque tienen dos ángulos iguales (recto y vertical). De su similitud se deduce que los módulos de los segmentos A1En el1 y AB se refieren como módulos de los segmentos de OB1 y OB.
Similar (basado en el mismo principio en dos ángulos) son dos triángulos más: COF y A1Fb1. En ellos, las relaciones iguales son ya de tales módulos de segmentos: A1En el1 con CO y Fb1con el OF. Según la construcción, los segmentos AB y CO serán iguales. Por lo tanto, los lados izquierdos de las igualdades de relaciones indicadas son los mismos. Por lo tanto, los derechos son iguales. Es decir, OB1 / S es igual Fb1/ OF.
En la igualdad indicada, los segmentos indicados por puntos pueden ser reemplazados por los conceptos físicos correspondientes. Entonces ov1 Es la distancia desde la lente a la imagen. OB es la distancia del sujeto a la lente. OF - longitud focal Un segmento Fb1 igual a la diferencia en distancia a la imagen y foco. Por lo tanto, se puede reescribir de otra manera:
f / d = (f - F) / F o Ff = df - dF.
Para derivar la fórmula de lente delgada, la última igualdad debe dividirse en dfF. Entonces resulta:
1 / d + 1 / f = 1 / F.
Это у есть формула тонкой собирающей линзы.Una distancia focal de dispersión es negativa. Esto lleva a un cambio en la igualdad. Es cierto, es insignificante. Solo en la fórmula de una lente de dispersión delgada, hay un signo menos delante de la relación 1 /F. Eso es:
1 / d + 1 / f = - 1 / F.
Condición La distancia focal de la lente colectora es de 0.26 m. Se requiere calcular su aumento si el sujeto está a una distancia de 30 cm.
Solución Comienza con la introducción de la notación y la traducción de unidades en C. Bien conocido d = 30 cm = 0.3 my F = 0.26 m. Ahora necesita seleccionar la fórmula, la principal que está indicada para la ampliación, la segunda - para una lente colectora delgada.
Necesitan ser combinados de alguna manera. Para hacer esto, tendrá que considerar el dibujo de la construcción de la imagen en la lente colectora. De estos triángulos queda claro que Γ = H / h= f / d. Es decir, para encontrar el aumento, debe calcular la relación entre la distancia a la imagen y la distancia al sujeto.
El segundo es conocido. Pero se supone que la distancia a la imagen se deriva de la fórmula indicada anteriormente. Resulta que
f = df / (d - F)
Ahora estas dos fórmulas deben combinarse.
R = df / (d(d - F)) = F / (d - F)
En este punto, resolver el problema de la fórmula de lente delgada se reduce a cálculos elementales. Queda por sustituir las cantidades conocidas:
G = 0.26 / (0.3 - 0.26) = 0.26 / 0.04 = 6.5.
Respuesta: la lente da un aumento de 6.5 veces.

Condición La lámpara se encuentra a un metro de la lente colectora. Se obtiene una imagen de su espiral en una pantalla a 25 cm de la lente. Calcule la distancia focal de la lente especificada.
La decisión. Se supone que debe escribir los siguientes valores en los datos: d = 1 my f = 25 cm = 0.25 m. Esta información es suficiente para calcular la distancia focal a partir de la fórmula de una lente delgada.
Entonces 1 /F = 1/1 + 1 / 0.25 = 1 + 4 = 5. Pero en el problema, es necesario conocer el enfoque y no la potencia óptica. Por lo tanto, solo queda dividir 1 por 5 y obtener la distancia focal:
F = 1/5 = 0,2 m
Respuesta: la distancia focal de la lente colectora es de 0.2 m.
Condición. La vela se colocó a una distancia de 15 cm de la lente colectora. Su potencia óptica es de 10 dioptrías. La pantalla detrás de la lente está configurada para que produzca una imagen clara de la vela. ¿A qué es igual esta distancia?
La decisión. En un registro corto se supone que debe escribir los siguientes datos: d = 15 cm = 0,15 m, D = 10 dioptrías La fórmula anterior debe escribirse con un ligero cambio. A saber, en el lado derecho de la igualdad, poner D en lugar de 1 /F.
Después de varias transformaciones, obtenemos la siguiente fórmula para la distancia desde la lente a la imagen:
f = d / (dd - 1)
Ahora necesita sustituir todos los números y contar. Resulta este valor para f: 0.3 m.
Respuesta: la distancia desde la lente a la pantalla es de 0.3 m.

Condición El objeto y su imagen están separados 11 cm. Una lente colectora proporciona un aumento de 3 veces. Encuentra su distancia focal.
La decisión. La distancia entre el objeto y su imagen está convenientemente indicada por la letra L = 72 cm = 0.72 m. Aumente G = 3.
Dos situaciones son posibles aquí.Primero: el sujeto está detrás del foco, es decir, la imagen es real. En el segundo, un objeto entre el foco y la lente. Entonces la imagen está en el mismo lado que el sujeto, e imaginaria.
Considera la primera situación. El sujeto y la imagen están en lados opuestos de la lente colectora. Aquí puedes escribir la siguiente fórmula: L = d + f. Se supone que la segunda ecuación escribe: G = f / d. Es necesario resolver el sistema de estas ecuaciones con dos incógnitas. Para hacer esto, reemplace L por 0.72 m, y Г por 3.
De la segunda ecuación resulta que f = 3d. Entonces el primero se convierte así: 0.72 = 4d. Fácil de contar d = 0,18 (m). Ahora fácil de detectar f = 0,54 (m).
Queda por usar la fórmula de lente delgada para calcular la distancia focal. F = (0.18 * 0.54) / (0.18 + 0.54) = 0.135 (m). Esta es la respuesta para el primer caso.
En la segunda situación, la imagen es imaginaria y la fórmula para L será diferente: L = f - d. La segunda ecuación para el sistema será la misma. Razonando de la misma manera, obtenemos que d = 0,36 (m), y f = 1,08 (m). Un cálculo similar de la distancia focal dará el siguiente resultado: 0,54 (m).
Respuesta: la distancia focal de la lente es 0.135 mo 0.54 m.
La trayectoria de los rayos en una lente delgada es importanteAplicación práctica de la óptica geométrica. Después de todo, se utilizan en muchos dispositivos, desde una lupa simple hasta microscopios y telescopios de precisión. Por lo tanto, necesita saber sobre ellos.
La fórmula derivada de una lente delgada permite resolvermuchas tareas Además, le permite sacar conclusiones sobre qué imagen dan diferentes tipos de lentes. En este caso, es suficiente saber su distancia focal y la distancia al sujeto.


























