
अंतरिक्ष में, विमान अलग-अलग सेट किया जा सकता हैतरीके (एक बिंदु और एक वेक्टर, दो बिंदु और एक वेक्टर, तीन बिंदु, आदि)। यह इस बात के साथ है कि विमान के समीकरण के विभिन्न रूप हो सकते हैं। इसके अलावा, अगर कुछ शर्तों को पूरा किया जाता है, तो विमान समानांतर, लंबवत, प्रतिच्छेदन आदि हो सकते हैं। हम इस लेख में इसके बारे में बात करेंगे। हम सीखेंगे कि विमान के सामान्य समीकरण और अधिक कैसे आकर्षित करें।
मान लीजिए कि एक अंतरिक्ष आर है3, जिसमें एक आयताकार XYZ समन्वय प्रणाली है। आइए हम एक वेक्टर α को परिभाषित करते हैं, जो प्रारंभिक बिंदु O से जारी किया जाएगा। वेक्टर α के अंत के माध्यम से, एक प्लेन P खींचें, जो इसके लिए लंबवत होगा।
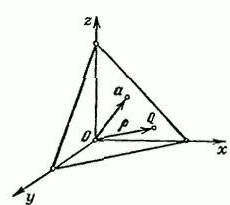
हम एक मनमाना बिंदु Q = (x, y, z) को दर्शाते हैं। हमें अक्षर P के साथ बिंदु Q के त्रिज्या वेक्टर पर हस्ताक्षर करते हैं। इस मामले में, वेक्टर α की लंबाई p = IαI और, = (cosα, cosγ, cosy) के बराबर है।
यह एक इकाई वेक्टर है जो इंगित करता हैओर, साथ ही वेक्टर α। α, are और γ वे कोण हैं जो वेक्टर the और अंतरिक्ष कुल्हाड़ियों x, y, z की सकारात्मक दिशाओं के बीच क्रमशः बनते हैं। वेक्टर a पर किसी भी बिंदु QϵП का प्रक्षेपण एक स्थिर मूल्य है, जो p: (p, () = p (p =0) के बराबर है।
उपरोक्त समीकरण समझ में आता है जब p = 0।केवल एक चीज यह है कि इस मामले में विमान P, बिंदु O (α = 0) को काट देगा, जो कि मूल है, और बिंदु O से उत्सर्जित इकाई वेक्टर direction अपनी दिशा के बावजूद, P से लंबवत होगी, जिसका अर्थ है कि सदिश determined संकेत के सटीक के साथ निर्धारित किया जाता है। पिछला समीकरण हमारे विमान P का समीकरण है, जिसे वेक्टर रूप में व्यक्त किया गया है। लेकिन निर्देशांक में, यह इस तरह दिखेगा:

P यहाँ 0. से अधिक या बराबर है। हमने सामान्य रूप में विमान के समीकरण को अंतरिक्ष में पाया है।
यदि निर्देशांक में समीकरण शून्य से गुणा नहीं किया जाता है, तो हमें दिए गए समीकरण के बराबर समीकरण मिलता है, जो उसी विमान को परिभाषित करता है। यह इस तरह दिखेगा:

यहाँ A, B, C एक ही समय में नॉनज़रो हैं। इस समीकरण को सामान्य विमान समीकरण के रूप में जाना जाता है।
सामान्य समीकरण को अतिरिक्त स्थितियों की उपस्थिति में संशोधित किया जा सकता है। आइए उनमें से कुछ पर एक नज़र डालें।
आइए हम मान लें कि गुणांक A 0. के बराबर है। इसका मतलब है कि यह विमान दिए गए अक्ष ऑक्स के समानांतर है। इस स्थिति में, समीकरण का रूप बदल जाएगा: Vu + Cz + D = 0।
इसी प्रकार, समीकरण का रूप निम्नलिखित परिस्थितियों में बदल जाएगा:
मामले में जब संख्या A, B, C, D गैर-शून्य होते हैं, तो समीकरण का रूप (0) इस प्रकार हो सकता है:
x / a + y / b + z / c = 1,
जिसमें a = -D / A, b = -D / B, c = -D / C।
नतीजतन, हमें सेगमेंट में विमान का समीकरण मिलता है। यह ध्यान देने योग्य है कि यह विमान निर्देशांक (a, 0,0), Oy - (0, b, 0), और Oz - (0,0, c) के साथ एक बिंदु पर ऑक्सी अक्ष को काट देगा।

समीकरण x / a + y / b + z / c = 1 को ध्यान में रखते हुए, किसी दिए गए निर्देशांक प्रणाली के सापेक्ष विमान के स्थान को नेत्रहीन रूप से दर्शाना आसान है।
प्लेन P के सामान्य वेक्टर n में निर्देशांक होते हैं जो इस प्लेन के सामान्य समीकरण के गुणांक होते हैं, यानी n (A, B, C)।

सामान्य एन के निर्देशांक निर्धारित करने के लिए, दिए गए विमान के सामान्य समीकरण को जानने के लिए पर्याप्त है।
एक लाइन खंड समीकरण का उपयोग करते समयप्रपत्र x / a + y / b + z / c = 1 है, जैसा कि सामान्य समीकरण का उपयोग करते समय, आप किसी दिए गए विमान के किसी भी सामान्य वेक्टर के निर्देशांक को लिख सकते हैं: (1 / a + 1 / b + 1 / सी)।
यह ध्यान देने योग्य है कि सामान्य वेक्टर मदद करता हैविभिन्न समस्याओं का समाधान करें। सबसे आम समस्याओं में विमानों की लंबवतता या समानांतरता को साबित करने की समस्या, विमानों के बीच के कोणों को खोजने की समस्या या विमानों और रेखाओं के बीच के कोण शामिल हैं।
किसी दिए गए प्लेन के लिए एक नॉनजरो वेक्टर n लंबवत किसी दिए गए विमान के लिए सामान्य (सामान्य) कहा जाता है।
मान लीजिए कि समन्वय स्थान (आयताकार समन्वय प्रणाली) में ऑक्सीज़ दिए गए हैं:

एक विमान के लिए एक समीकरण तैयार करना आवश्यक है जो बिंदु n से गुजरता है और सामान्य n से सीधा होता है।
अंतरिक्ष में, हम किसी भी मनमाना बिंदु को चुनते हैं औरहम इसे M (xy, z) द्वारा निरूपित करते हैं। किसी भी बिंदु M (x, y, z) का त्रिज्या सदिश r = x * i + y * j + z * k है, और बिंदु Mₒ का त्रिज्या सदिश (xₒ, yₒ, zₒ) - rₒ = x of * है i + yₒ * j + zₒ * k बिंदु M दिए गए विमान का होगा यदि वेक्टर МₒМ वेक्टर n के लंबवत है। आइए हम डॉट उत्पाद का उपयोग करके ऑर्थोगोनलिटी की स्थिति लिखें
[एमएम, एन] = ०।
चूंकि М SinceМ = r - rₒ, विमान का वेक्टर समीकरण इस तरह दिखेगा:
[r - rₒ, n] = 0
इस समीकरण का दूसरा रूप हो सकता है।इसके लिए, डॉट उत्पाद के गुणों का उपयोग किया जाता है, और समीकरण के बाईं ओर रूपांतरित किया जाता है। [r - r], n] = [r, n] - [r n, n]। यदि [r,, n] को c के रूप में निरूपित किया जाता है, तो हमें निम्नलिखित समीकरण मिलते हैं: [r, n] - c = 0 या [r, n] = c, जो कि त्रिज्या वैक्टर के सामान्य वेक्टर पर अनुमानों की गति को व्यक्त करता है। दिए गए बिंदु जो विमान के हैं।
अब आप हमारे विमान के वेक्टर समीकरण [r - r get, n] = 0. से r - rₒ = (x - xₒ) * i + (y - yₒ) * j + (z - zₒ) लिखने का समन्वित रूप प्राप्त कर सकते हैं। ) * k, और n = A * i + B * j + C * k, हमारे पास है:

यह पता चला है कि हमारे पास एक समतल बिंदु है जो सामान्य n पर लंबवत बिंदु से होकर गुजरता है:
A * (x- xₒ) + B * (y- y C) C * (z - zₒ) = 0।
आइए हम दो मनमाना अंक निर्धारित करें M '(x', y ', z') और M two (x ″, y y, z,), साथ ही एक वेक्टर a (a, a, a)।
अब हम दिए गए समतल के लिए एक समीकरण बना पाएंगे, जो मौजूदा बिंदुओं ′ M और M to से होकर गुजरेगा, साथ ही दिए गए वेक्टर a के समानांतर निर्देशांक (x, y, z) के साथ किसी भी बिंदु M को पार करेगा।
इसके अलावा, वैक्टर M′M = {x-x y; y-y ′; zz ′} और M ″ M = {x x -x ′; y ″ -y ′; z ″ -z ′} वेक्टर के साथ मैथुन करना चाहिए a = (ए, ए, ए, ए), जिसका अर्थ है कि (एमएम, एम, एम, ए) = 0।
तो, अंतरिक्ष में एक विमान का हमारा समीकरण इस तरह दिखेगा:
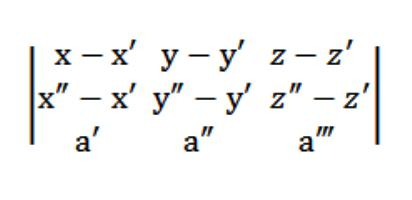
मान लीजिए कि हमारे तीन अंक हैं:(x ′, y ′, z ′), (x y, y z, z ″), (x, y x, z that) जो एक सीधी रेखा से संबंधित नहीं हैं। दिए गए तीन बिंदुओं से गुजरने वाले विमान के समीकरण को लिखना आवश्यक है। ज्यामिति का सिद्धांत यह दावा करता है कि इस तरह का विमान वास्तव में मौजूद है, लेकिन यह एकमात्र और अभेद्य है। चूँकि यह विमान बिंदु (x ′, y ′, z,) को काटता है, इसके समीकरण का रूप इस प्रकार होगा:

यहाँ A, B, C एक ही समय में नॉनज़रो हैं। इसके अलावा, दिए गए समतल में दो और बिंदु होते हैं: (x y, y z, z given) और (x ‴, y ‴, z ‴)। इस संबंध में, निम्नलिखित शर्तें पूरी होनी चाहिए:

अब हम अज्ञात यू, वी, डब्ल्यू के साथ समीकरणों (रैखिक) के एक सजातीय प्रणाली की रचना कर सकते हैं:

हमारे मामले में, x, y या z मनमाना हैवह बिंदु जो समीकरण (1) को संतुष्ट करता है। समीकरण (1) और समीकरणों की प्रणाली (2) और (3) को ध्यान में रखते हुए, ऊपर की आकृति में इंगित समीकरणों की प्रणाली वेक्टर एन (ए, बी, सी) से संतुष्ट है, जो कि nontrivial है। इसीलिए इस प्रणाली का निर्धारक शून्य के बराबर है।
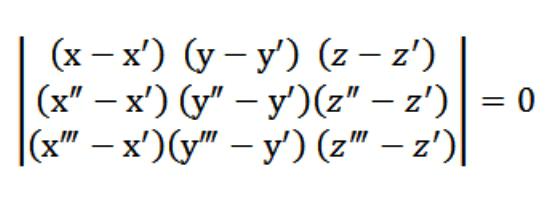
समीकरण (1), जो हमें मिला है, हैसमतल का समीकरण है। यह बिल्कुल 3 बिंदुओं से गुजरता है, और यह जांचना आसान है। ऐसा करने के लिए, हमें पहली पंक्ति में स्थित तत्वों द्वारा अपने निर्धारक का विस्तार करने की आवश्यकता है। निर्धारक के मौजूदा गुणों से यह निम्न है कि हमारा विमान एक साथ तीन आरंभिक बिंदुओं (x ′, y ′, z ′), (x ″, y ″, z z), (x ‴, y ‴, z ‴) को एक साथ काटता है। । यानी हमने अपने सामने निर्धारित कार्य को हल कर लिया है।
डायहेड्रल कोण हैदो आधे विमानों द्वारा गठित एक स्थानिक ज्यामितीय आकृति जो एक सीधी रेखा से निकलती है। दूसरे शब्दों में, यह अंतरिक्ष का एक हिस्सा है जो इन आधे विमानों द्वारा सीमित है।
मान लें कि हमारे पास दो समीकरण हैं:
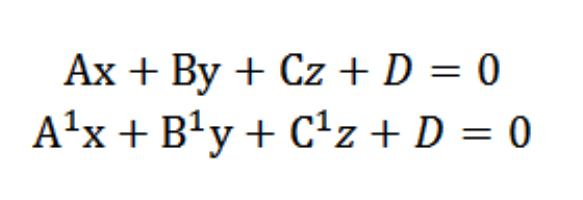
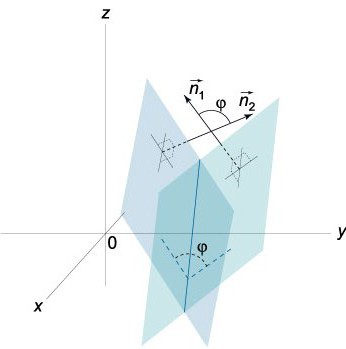
हम जानते हैं कि वैक्टर एन = (ए, बी, सी) औरदिए गए विमानों के अनुसार N = (А¹, В¹, С¹) लंबवत हैं। इस संबंध में, वैक्टर एन और एन equal के बीच का कोण (कोण (डायहेड्रल) के बराबर है, जो इन विमानों के बीच है। डॉट उत्पाद है:
NN N = | N || N¹ | cos |,
ठीक है क्योंकि
cos = NNφ / | N || Nφ = (AA¹ + BB¹ + CC N) / ((((A² + B² + C²)) * (√ (A¹) ¹ + (B¹) ² + (C¹) ¹) |
यह ध्यान में रखना पर्याप्त है कि 0 into।
वास्तव में, दो विमान जो प्रतिच्छेद करते हैं, दो कोण (विकर्ण) बनाते हैं: that1 और φ2... इनका योग π (π) के बराबर होता है1+ φ2= π)। उनके कोसाइन के लिए, उनके पूर्ण मूल्य समान हैं, लेकिन वे संकेतों में भिन्न होते हैं, अर्थात, φ1= -सर φ2... यदि समीकरण (0) में हम A, B और C को क्रमशः -A -B और -C से प्रतिस्थापित करते हैं, तो हमें जो समीकरण मिलेगा, वही समतल को निर्धारित करेगा, समीकरण cos N = NN में एकमात्र कोण)1/ | एन || एन1| be-φ द्वारा प्रतिस्थापित किया जाएगा।
विमानों को लंबवत कहा जाता है, बीच मेंकोण 90 डिग्री है। ऊपर उल्लिखित सामग्री का उपयोग करके, हम एक विमान के समीकरण को दूसरे के लंबवत पा सकते हैं। मान लें कि हमारे पास दो विमान हैं: Ax + By + Cz + D = 0 और A +x + B¹y + C =z + 1 = 0। हम यह कह सकते हैं कि यदि वे cos 0 = 0 हैं तो वे लंबवत होंगे। इसका अर्थ है कि NN means = AA¹ + BB that + CC 0 = 0।
समानांतर दो विमान हैं जिनमें सामान्य बिंदु नहीं होते हैं।
विमानों की समानता (उनके समीकरणों) के लिए शर्तपिछले भाग की तरह ही) वेक्टर N और N which, जो उनके लिए लंबवत हैं, समवर्ती हैं। इसका अर्थ है कि निम्नलिखित आनुपातिकता की शर्तें पूरी होती हैं:
ए / ए¹ = बी / बी¹ = सी / सी B।
यदि आनुपातिक स्थिति को बढ़ाया जाता है - A / A B = B / B C = C / Cional = DD¹,
यह इंगित करता है कि ये विमान संयोग करते हैं। और इसका मतलब है कि समीकरण Ax + By + Cz + D = 0 और A +x + B¹y + C¹z + D one = 0 एक विमान का वर्णन करते हैं।
मान लीजिए हमारे पास एक प्लेन P है, जो दिया गया हैसमीकरण (को ०)। निर्देशांक (xₒ, yₒ, zₒ) = Qₒ के साथ बिंदु से इसकी दूरी का पता लगाना आवश्यक है। ऐसा करने के लिए, आपको प्लेन पी के समीकरण को एक सामान्य रूप में लाने की आवश्यकता है:
(p, v) = p (p≥0)।
इस मामले में, ρ (x, y, z) हैP पर स्थित हमारे बिंदु Q की त्रिज्या वेक्टर, लंबवत P की लंबाई है, जिसे शून्य बिंदु से जारी किया गया था, v इकाई वेक्टर है, जो दिशा में स्थित है।

कुछ बिंदु Q की त्रिज्या वेक्टर के अंतर ρ-ρº0= (x such, yₒ, zₒ) एक ऐसा सदिश राशि है, जिसका प्रक्षेपण का पूर्ण मान v पर दूरी d के बराबर है, जिसे Q से प्राप्त किया जाना चाहिए0= (x P, yₒ, zₒ) से P:
डी = | (ρ-ρ0, v) | लेकिन
(ρ-ρ0, v) = (ρ, v) - (ρ)0, v) = р– (ρ)0, v)।
तो यह पता चला है
d = | (ρ)0, v) -p |
अब क्यू से दूरी d की गणना करने के लिए देखा गया है0 विमान P के लिए, आपको p के बाईं ओर स्थानांतरित करते हुए, और x, y, z के बजाय अंतिम में x (yₒ, zₒ) को स्थानांतरित करते हुए, विमान के समीकरण के सामान्य रूप का उपयोग करने की आवश्यकता है।
इस प्रकार, हम परिणामी अभिव्यक्ति का पूर्ण मान पाएंगे, अर्थात वांछित डी।
पैरामीटर भाषा का उपयोग करके, हमें स्पष्ट मिलता है:
d = | Ax / + Byₒ + Cz | | / ² (A² + B² + C²) |
यदि दिया गया बिंदु Q0 विमान पी के दूसरी तरफ है, मूल की तरह, फिर वेक्टर ρ-ρ के बीच0 और v एक प्रसूति कोण है, इसलिए:
डी = - (ρ-ρ0, v) = (ρ)0, v) -प> ०।
मामले में जब बिंदु क्यू0 साथ में निर्देशांक की उत्पत्ति पी के एक ही तरफ स्थित है, तो निर्मित कोण तीव्र है, अर्थात:
d = (ρ-ρ0, v) = p - (p)0, v)> 0।
नतीजतन, यह पता चला है कि पहले मामले में (ρ)0, v)> р, दूसरे में (ρ)0, v) <p।
स्पर्शरेखा M the के बिंदु पर सतह पर जाने वाला स्पर्शरेखा तल सतह पर इस बिंदु के माध्यम से खींचे गए वक्रों के लिए हर संभव स्पर्शरेखा युक्त विमान है।
सतह F (x, y, z) = 0 के समीकरण के इस रूप के साथ स्पर्शरेखा बिंदु M tang (xº, yº, zº) पर स्पर्शरेखा तल का समीकरण इस तरह दिखेगा:
एफएक्स(x (, yº, zº) (x- x +) + Fएक्स(x (, yº, zº) (y- y +) + Fएक्स(x (, yº, zº) (z-z =) = 0।
यदि हम सतह को स्पष्ट रूप से z = f (x, y) में सेट करते हैं, तो स्पर्शरेखा विमान समीकरण द्वारा वर्णित किया जाएगा:
z-zº = f (xº, yº) (x- x +) + f (xº, yº) (y-y ()।
प्रणाली तीन आयामी अंतरिक्ष में स्थित हैनिर्देशांक (आयताकार) ऑक्सीज़, दो विमानों पी P और पी given दिए गए हैं, जो अंतरंग होते हैं और संयोग नहीं करते हैं। चूंकि आयताकार समन्वय प्रणाली में कोई भी विमान सामान्य समीकरण द्वारा निर्धारित किया जाता है, हम मान लेंगे कि P ′ और P + समीकरणों द्वारा दिए गए हैं Ax + B′y + C′z + D 0 = 0 और A + x + ″ y + C ″ z + D 0 = 0। इस स्थिति में, हमारे पास P n समतल का सामान्य n ′ (A B, B C, C,) और P ″ तल का सामान्य n ″ (A ″, B ″, C have) है। चूंकि हमारे विमान समानांतर नहीं हैं और संयोग नहीं करते हैं, इसलिए ये वैक्टर नहीं मिलते हैं। गणित की भाषा का उपयोग करते हुए, हम इस स्थिति को निम्नानुसार लिख सकते हैं: n ≠, n ↔ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ, C ″), λϵR। P P और P inters के चौराहे पर स्थित सीधी रेखा को अक्षर a से निरूपित किया जाएगा, इस स्थिति में a = P ∩ lies P lies।
a एक सीधी रेखा है जिसमें सभी बिंदुओं का एक सेट होता है(सामान्य) विमानों पी ′ और पी ′। इसका अर्थ है कि सीधी रेखा से संबंधित किसी भी बिंदु के निर्देशांक को एक साथ A'x + B'y + C'z + D '= 0 और A + x + B + y + C + z + D inates के समीकरणों को पूरा करना चाहिए। = 0। इसका मतलब है कि बिंदु के निर्देशांक समीकरणों की निम्नलिखित प्रणाली का एक विशेष समाधान होंगे:

नतीजतन, यह पता चला है कि इस का समाधान (सामान्य)समीकरणों की प्रणाली सीधी रेखा के प्रत्येक बिंदुओं के निर्देशांक का निर्धारण करेगी, जो P ″ और P ″ के प्रतिच्छेदन बिंदु के रूप में कार्य करेगा, और अंतरिक्ष में ऑक्सीज़ समन्वय प्रणाली (आयताकार) में सीधी रेखा का निर्धारण करेगा।


























