Hogyan lehet megtalálni a függvény minimális és maximális pontját: szolgáltatások, módszerek és példák

Funkciója és jellemzőinek kutatása szükségesa modern matematika egyik legfontosabb fejezete. Bármely függvény fõ alkotóeleme olyan grafikonok, amelyek nemcsak tulajdonságait, hanem ennek a függvénynek a származékának paramétereit ábrázolják. Vizsgáljuk meg ezt a nehéz témát. Szóval, mi a legjobb módszer a funkció maximális és minimális pontjainak megkeresésére?

Funkció: Meghatározás

Bármely változót, amely valamilyen módon függ egy másik mennyiség értékétől, függvénynek lehet nevezni. Például az f (x²) kvadratikus, és meghatározza az x teljes halmaz értékeit. Tegyük fel, hogy x = 9, akkor függvényünk értéke 9²= 81.

A funkciók sokféle formában vannak:logikai, vektor, logaritmikus, trigonometrikus, numerikus és mások. Olyan kiemelkedő elmék, mint Lacroix, Lagrange, Leibniz és Bernoulli, részt vettek tanulmányaikban. Munkáik erőssé válnak a funkciók tanulásának modern módszereiben. Mielőtt megtalálná a minimális pontokat, nagyon fontos megérteni a függvény és annak származéka jelentését.

Származék és szerepe

Minden funkció függ a működésétőlváltozók, ami azt jelenti, hogy bármikor megváltoztathatják értéküket. A grafikonon ezt egy görbeként ábrázoljuk, amely ekkor leesik, majd az ordináta mentén emelkedik (ez az egész "y" számkészlet a gráf függőleges mentén). Tehát a függvény maximális és minimális pontjának meghatározása pontosan kapcsolódik ezekhez a „ingadozásokhoz”. Magyarázza el, mi ez a kapcsolat.

Bármely függvény derivációját ábrázoljuk.annak fő jellemzőinek tanulmányozása és a függvény változásának kiszámítása érdekében (vagyis megváltoztatja az értékét az "x" változótól függően). Abban a pillanatban, amikor a függvény növekszik, a derivatív gráfja is növekedni fog, de bármelyik másodpercben a függvény csökkenni kezdhet, majd a derivált gráfja csökken. Azokat a pontokat, ahol a derivatívum mínuszjelről pluszra megy át, minimum pontoknak nevezzük. A minimális pontok megtalálásának ismerete érdekében jobban meg kell értenie a derivált fogalmát.

Hogyan lehet kiszámítani a deriváltot?

A derivált függvény meghatározása és kiszámításatöbb fogalmat von le a differenciálszámításból. Általában a származék meghatározása a következőképpen fejezhető ki: ez az a mennyiség, amely megmutatja a függvény változásának sebességét.

A matematikai módszer annak meghatározására sokak számáraA hallgatók bonyolultnak tűnnek, de valójában minden sokkal egyszerűbb. Bármely függvény deriváltjának megtalálásához csak a szokásos tervet kell követni. Az alábbiakban leírjuk, hogyan lehet megtalálni a függvény minimális pontját differenciálódási szabályok alkalmazása nélkül és a derivatívák táblájának megjegyzése nélkül.

1. A függvény deriváltja kiszámítható az alábbiakkalgrafika. Ehhez magát a függvényt kell ábrázolni, majd egy pontot vegyen rá (az ábrán az A pont) Rajzoljon egy vonalat függőlegesen az abszcissza tengelyig (x pont₀), és az A pontban rajzoljon egy érintőt a gráfhozfunkciót. Az abszcissza és az érintő tengely egy bizonyos szöget alkot. Annak kiszámításához, hogy a függvény milyen gyorsan növekszik, ki kell számítani ennek a szögnek az érintőjét.
2. Kiderült, hogy az érintő és aaz x tengely iránya a függvény derivációja egy kis területen, az A ponttal. Ezt a módszert a deriváció meghatározásának geometriai módszerének tekintik.

Funkciókutatás módszerei

Az iskolai matematikai programban ez lehetségeskétféle módon meg lehet találni egy függvény minimális pontját. Az első módszert már a gráf segítségével elemeztük, de hogyan lehet meghatározni a származék numerikus értékét? Ehhez meg kell tanulnia több olyan képletet, amelyek leírják a derivátum tulajdonságait, és segítenek az "x" típusú változókat számokká konvertálni. A következő módszer univerzális, ezért szinte mindenféle funkcióra alkalmazható (mind geometriai, mind logaritmikus).

1. A függvényt a derivatív függvénnyel kell egyenértékűvé tenni, majd egyszerűsíteni a kifejezést a differenciálás szabályainak felhasználásával.
2. Bizonyos esetekben, amikor egy függvényt megadnak, inahol az "x" változó az elválasztóban van, meg kell határozni a megengedett értékek tartományát a "0" pont kizárásával (annak az egyszerű okból, hogy a matematikában semmiképpen sem osztható nullával).
3. Ezt követően át kell konvertálnia a függvény eredeti formáját egyszerű egyenletre, egyenlővé téve a teljes kifejezést nullával. Például, ha a függvény így néz ki: f (x) = 2x³+ 38x, akkor a differenciálódási szabályok szerint származéka f "(x) = 3x²1. Ezután ezt a kifejezést a következő alak egyenleté alakítjuk: 3x²+1 = 0.
4. Az egyenlet megoldása és az "x" pontok megtalálása után,ábrázolják őket az abszcisszán és meghatározzák, hogy a derivált ezekben a területeken a megjelölt pontok között pozitív vagy negatív-e. A kijelölés után világossá válik, hogy a függvény mikor kezd csökkenni, vagyis megváltoztatja a jelet mínuszról ellenkezőre. Ilyen módon találhatja meg a minimális és a maximális pontokat is.

Differenciálási szabályok

Самая основная составляющая в изучении функции и származéka a megkülönböztetés szabályainak ismerete. Csak nagy segítségükkel alakíthatók át a terjedelmes kifejezések és a nagy komplex funkciók. Ismerkedjünk meg velük, nagyon sok van, de mind nagyon erősek, mind a teljesítmény, mind a logaritmikus függvények szabályos tulajdonságainak köszönhetően.

1. Bármely állandó deriváltja nulla (f (x) = 0). Vagyis az f (x) = x derivált⁵A + x - 160 formája a következő: f "(x) = 5x⁴1.
2. Két kifejezés összegének származéka: (f + w) "= f" w + fw ".
3. Logaritmikus függvény deriváltja: (log_ésd) "= d / ln a * d. Ez a képlet mindenféle logaritmusra vonatkozik.
4. Származékos fok: (xⁿ) "= n * x^N-1. Például (9x²) "= 9 * 2x = 18x.
5. A szinuszos függvény derivációja: (sin a) "= cos a. Ha az a szög sinje 0,5, akkor a derivativációja √3 / 2.

Extremum pontok

Már kitaláltuk, hogyan lehet megtalálni a minimális pontokat,létezik azonban a függvény maximális pontjának fogalma. Ha a minimum azt a pontot jelöli, amelyen a függvény a mínuszjektől a pluszig mozog, akkor a maximális pontok azok az abszcissza tengelyen lévő pontok, ahol a függvény deriváltja pluszról az ellenkezőre változik - mínusz.

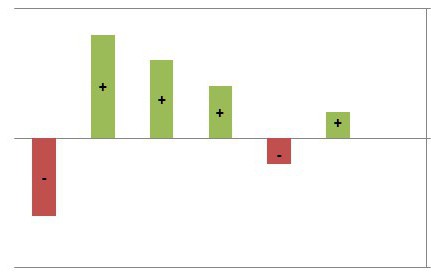
A maximális pontokat a fent leírt módszerrel lehet megtalálni, csak figyelembe kell venni, hogy azok azokat a szakaszokat jelölik, amelyekben a függvény csökkenni kezd, vagyis a derivátum nulla alatt van.

A matematikában szokásos mindkét fogalmat általánosítani,helyettesítve őket a "szélsőséges pontok" kifejezéssel. A feladat ezen pontjainak meghatározására való felkéréskor ez azt jelenti, hogy ki kell számítani ennek a függvénynek a derivatíváját, és meg kell találni a minimális és a maximális pontot.