
A háromszög az egyik leggyakoribbgeometriai alakzatok, amelyekkel az általános iskolában ismerünk. A háromszög területének felkutatása, a diákok geometriai leckékkel találkoznak. Szóval, mi a jellemzője annak, hogy a terület azonosítható legyen? Ebben a cikkben megvizsgáljuk az ilyen feladat elvégzéséhez szükséges alapvető képleteket, valamint elemezzük a háromszögek típusait.

A háromszög területét teljesen különböző módon találhatja meg, mivel a geometriában többféle forma van, amely három sarkot tartalmaz. Ezek a típusok a következők:
Nézzük részletesebben az összes létező háromszögtípust.

Az ilyen geometriai forma a leginkább tekinthetőgyakori a geometriai problémák megoldásában. Amikor szükség van egy tetszőleges háromszög rajzolására, akkor ez a lehetőség a mentésre kerül.
Egy éles szögű háromszögben, amint azt a neve is sugallja, az összes szög éles és 180 ° -ot eredményez.
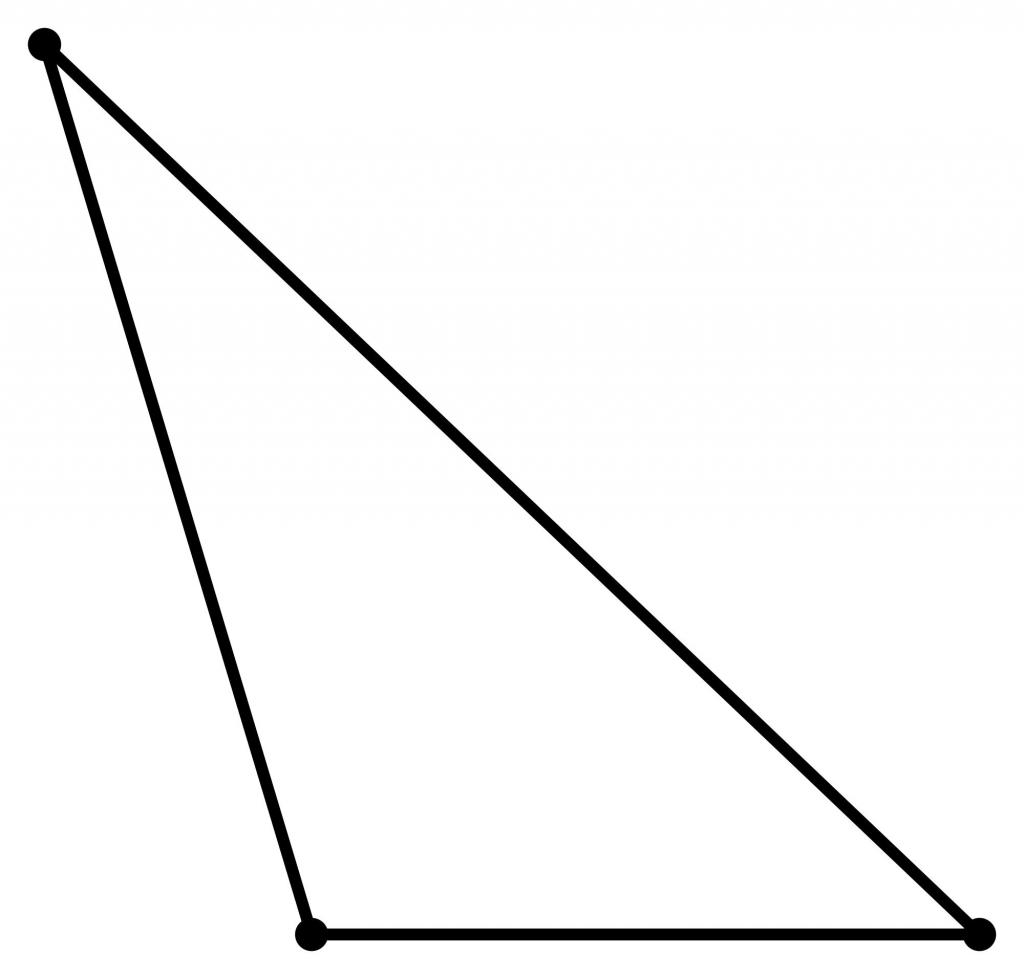
Egy ilyen háromszög is nagyon gyakori,ez azonban kissé ritkább, mint az akut szög. Például háromszögek (azaz több oldalának és szögének ismerete és a fennmaradó elemek megkeresése több oldalról is ismert) megoldásakor néha meg kell határozni, hogy a szög tompított-e vagy sem. A ferde szög koszinus negatív szám.
Egy tompa háromszögben az egyik szög értéke meghaladja a 90 ° -ot, tehát a fennmaradó két szög kis értékeket vehet fel (például 15 ° vagy akár 3 °).
Az ilyen típusú háromszög területének meghatározásához meg kell ismernie néhány árnyalatokat, amelyekről később beszélünk.
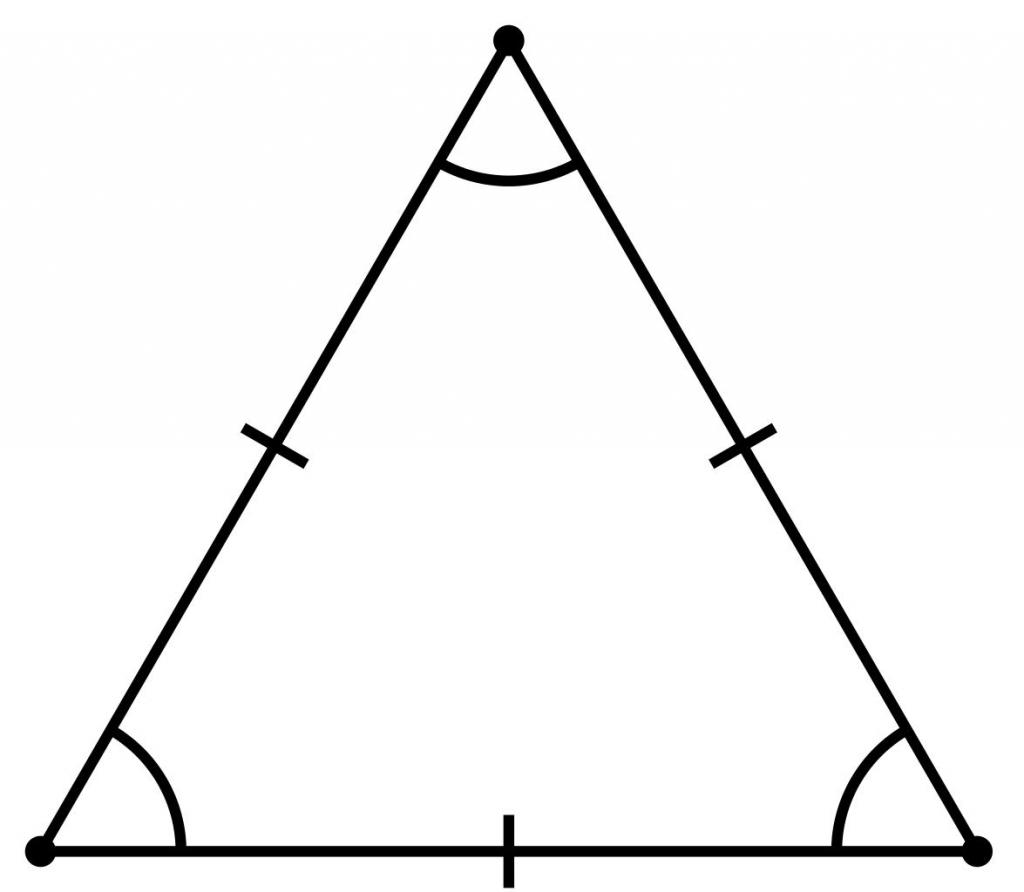
A szabályos sokszög egy alak,beleértve n szöget is, amelyekben az összes oldal és a szög egyenlő. Ez a szabályos háromszög. Mivel a háromszög összes szöge összege 180 °, akkor a három szög mindegyike 60 °.
A szabályos háromszöget tulajdonsága miatt egyenlő oldalú alaknak is hívják.
Érdemes megjegyezni, hogy egy szabályos háromszögben csak egy kör írható be, és csak egy kör írható le körül, és középpontjaik egy ponton helyezkednek el.

Az egyenlő oldalú típuson kívül meg is különböztethetjük megegyenlő szárú háromszög, kissé különbözik tőle. Egy ilyen háromszögben a két oldal és a két szög megegyezik egymással, és a harmadik oldal (amelyhez az egyenlő szögek szomszédosak) az alap.
Az ábra egy egyenlő szárú DEF háromszöget mutat, amelynek D és F szöge egyenlő, és DF az alap.

A derékszögű háromszöget azért nevezték el, mert annak egyik szöge egyenes, vagyis 90 ° -kal egyenlő. A másik két szög 90 ° -kal növekszik.
Egy ilyen háromszög legnagyobb oldala, amely 90 ° -os szöget zár be, a hipotenusz, míg a másik két oldal lába. Az ilyen típusú háromszögek esetében a Pythagorói tétel alkalmazható:
A lábak négyzethosszának összege megegyezik a hypotenuse négyzethosszával.
Az ábra egy BAC derékszögű háromszöget ábrázol AC hipotenuussal és AB és BC lábakkal.
A derékszögű háromszög területének megkereséséhez meg kell ismerni a lábak numerikus értékeit.
A képletekhez fordulunk ezen ábra területének meghatározásához.
A geometria szerint két képlet létezikalkalmas a legtöbb típusú háromszög területének meghatározására, nevezetesen az éles szögű, tompa, szabályos és egyenlő szárú háromszögekhez. Mindegyiket elemezzük.
Ez a formula univerzálisa számok által figyelembe vett terület megkeresése. Ehhez elegendő tudni az oldal hosszát és a rá húzott magasság hosszát. Maga a képlet (az alap magasságának fele) a következő:
S = ½ * A * H,
ahol A az adott háromszög oldala, és H a háromszög magassága.

Például az ACB hétszögű háromszög területének meghatározásához meg kell szorozni annak AB oldalát a CD magassággal, és el kell osztani a kapott értéket kettővel.
A terület megtalálása azonban nem mindig könnyű.háromszög ilyen módon. Például ahhoz, hogy ezt a képletet tompa háromszöghez használjuk, folytatnunk kell annak egyik oldalát, és csak ezután rajzoljunk magasságot rajta.
A gyakorlatban ezt a képletet többször használják, mint mások.
Ez a képlet, az előzőhöz hasonlóan, megfelelőA legtöbb háromszög és jelentéseik szerint a képlet következménye a háromszög oldalán és magasságában található terület meghatározására. Vagyis a vizsgált képlet könnyen levezethető az előzőből. Megfogalmazása így néz ki:
S = ½ * sinO * A * B,
ahol A és B a háromszög oldalai, és O az A és B oldalai közötti szög.
Emlékezzünk arra, hogy a szög szinuszát a kiemelkedő szovjet matematikus, V. M. Bradis nevéhez tartozó speciális táblában találhatjuk.
Most térjünk át más képletekhez, amelyek csak kivételes típusú háromszögekhez használhatók.
Az egyetemes képlet mellett, amely magában foglalja a háromszög magasságának rajzolásának szükségességét, a derékszögű háromszög területe a lábai között is megtalálható.
Tehát egy derékszögű háromszög területe a lábak szorzatának fele, vagy:
S = ½ * a * b,
ahol a és b egy derékszögű háromszög lábai.
Az ilyen típusú geometriai alakzatok abban különböznek egymástólhogy területe csak az egyik oldalának feltüntetett értékével található meg (mivel a szabályos háromszög minden oldala egyenlő). Tehát, miután elvégeztük a „háromszög területének meghatározása, ha az oldalak azonosak” feladatot, a következő képletet kell használniuk:
S = a2* √3 / 4,
ahol A egy egyenlő oldalú háromszög oldala.
A háromszög területének meghatározására az utolsó lehetőség a Heron formula. Használatához tudnia kell az ábra három oldalának hosszát. Heron képlete így néz ki:
S = √p · (p - a) · (p - b) · (p - c),
ahol a, b és c egy adott háromszög oldalai.
Néha egy feladatban megadják:"Egy szabályos háromszög területe az, hogy megtalálja oldalának hosszát." Ebben az esetben a már ismert képletet kell használnunk egy szabályos háromszög területének megkeresésére, és az oldal (vagy annak négyzetének) értékéből származtatni:
A2 = 4S / √3.
A GIA matematikai problémáiban számos formula található. Ezenkívül elég gyakran meg kell találni a háromszög területét kockás papíron.
Ebben az esetben a legkényelmesebb az ábra egyik oldalára magasságot felhívni, annak hosszát meghatározni a cellákból, és az univerzális képlettel megkeresni a területet:
S = ½ * A * H
Tehát a cikkben szereplő képletek tanulmányozása után nem lesz problémája bármilyen háromszög területének megtalálásával.


























