
יש תקופה שבה מתמטיקההמורה מתחיל להסביר מהן השברים הנכונים. ברגע זה התלמיד פותח שורה שלמה של משימות ותרגילים חדשים, ליישומם אתה צריך "להתאמץ". לא כל התלמידים מבינים נושא זה בפעם הראשונה, אך אנו ננסה להסביר הכל בשפה ברורה. אחרי הכל, למעשה, אין כאן שום דבר מורכב ונורא.
בכל צעד, אדם נתקל בסיטואציות בשאתה צריך להפריד ולחבר בין אובייקטים וחלקיהם. בין אם אנו קוצצים בול עץ או חותכים עוגה, בוחרים בבנק עם אחוז ההכנסה הגבוה ביותר, או אפילו מסתכלים על הזמן, השברים הנכונים מחכים לנו בכל מקום. זהו, בעצם, רק שבריר, שבר - הערך העליון מראה לנו כמה חלקים יש לנו, והתחתון - כמה מהם נדרשים כדי לקבל ערך שלם.
לפני שאתה מבין כיצד לתקן את השבר השגוי, עליך להבין סוגיות מהותיות יותר. כלומר - על מה אנחנו מדברים?
קחו דוגמה מחיי היומיום.קח את העוגה, חתוך לחתיכות זהות - כל אחת מהן, למעשה, תהיה החלק הנכון, כלומר חלק מחלקה שלמה. מה קורה אם נרכיב את כל השברים? עוגה שלמה אחת. אבל מה אם יש יותר חלקים מהנדרש? שילבנו את החלקים, קיבלנו פשטידה שלמה, וגם אלה הנוספים נשארו!

מבחינה מתמטית קיבלנוהשבר השגוי הוא כאשר החלקים בסך הכל נותנים ערך הגבוה מאחד. לדעת זאת בבעיה או במשוואה זה קל מתמיד. החלק התחתון - המכנה - יש לו פחות מהחלק העליון - המונה. ואם המספר התחתון גדול מהקודם העליון, אז זהו השבר הנכון.
כך שאדם רוצה ללמוד נושא כלשהואו נושא ספציפי, עליו להכיר בערך המעשי של המידע החדש. בשביל מה השברים הנכונים והלא נכונים? היכן משתמשים בהן? אי אפשר לעבוד עם ביטויים מתמטיים בלי לדעת שברים. ובמדעים אחרים אי אפשר להסתדר בלי מידע כזה: לא בכימיה, לא בפיזיקה, גם לא בכלכלה, ואפילו לא בסוציולוגיה או בפוליטיקה!

אנו כבר יודעים מה השבר הנכון.והטעות היא כזו שבה המונה גדול מהמכנה. מסתבר שיש לנו מספר שלם וחלק נוסף. למה לא פשוט לכתוב הכל בצורה הזו? זה ייקרא מספר מעורב.

ניקח לדוגמא את 5/2.כדי לקבל מספר מעורב, עלינו להפחית את המכנה מהמונה כמה פעמים שהוא מתאים לשם. במקרה זה, פעמיים, וכתוצאה מכך נקבל שני מספרים שלמים ושנייה אחת. המרה כזו היא תרגום של שבר שגוי לנכון. כאשר במקום הנוסח "שלוש שניות", אנו מקבלים את הביטוי "שלם ושנייה אחת", אנו מגיעים לצורה בצורה של מספר מעורב.
בעזרת שברים, אתה יכול לבצע את כל אותן פעולות,כמו במספרים שלמים: חיבור, חיסור, כפל, חלוקה. בהמשך תלמד כיצד לגדל לעוצמה, לחלץ שורשים מרובעים וקוביות, לקחת לוגריתמים. בינתיים עלינו ללמוד כיצד לבצע את הפעולות הפשוטות ביותר עם שברים נכונים ושגויים.

כאשר מתחלקים זה יהיה כמעט זהה, רק הרכיב השני בביטוי "מתהפך": (1/2) / (2/3) = (1/2) * (3/2) = 3/4.
כשמוסיפים ומחסירים, אפשר עם אותו הדברקל להשתמש גם במספרים מעורבים וגם בשברים לא תקינים (אם הבחירה מתרחשת). זה ידרוש הבאת התנאים למכנה משותף.

איך אוכל לעשות זאת?אם אתה זוכר את המאפיין הבסיסי של שבר, אז אתה יודע את התשובה - עליך להכפיל את שני השברים במספרים כאלה כדי שיהיו להם אותם ערכים בתחתית. לדוגמא, ישנם הערכים הבאים: 1/3 ו- 1/7. בהתאם לכלל, אנו מכפילים את השבר הנכון 1/3 ב- 7 ו- 1/7 ב- 3. אנו מקבלים 7/21 ו- 3/21. כעת ניתן להוסיף את המספרים ללא הפרעה: (7 + 3) / 21 = 10/21.
אך אינך צריך להכפיל במכנה הסמוךתמיד - אם היה לנו 1/4 ו- 1/8, יהיה קל יותר להכפיל את המונח הראשון ב -2, וזה הסוף שלו: 2/8 + 1/8 = 3/8. ההפרש מחושב באותו אופן.
התלמידים מבינים בקלות את נושא הטעותשברים נכונים. מה כל כך קשה? אם אכן מתרחשות טעויות, זה כמעט תמיד בגלל חוסר תשומת לב - המכנה המשותף נמצא באופן שגוי, למשל. יש, כמובן, טעות פופולרית אחת, והיא מותרת במשוואות.

אתה יכול לכתוב שברים אנכיים, אבל אתה יכול -אופקית. במקרה הראשון, משהו נראה כמו עמודה, שבה אנו מקבלים מלמעלה למטה: המספר הראשון, קו אופקי, המספר השני. ואם הקו צר ולא ניתן "להתנדנד" בגובה, אז אתה יכול לכתוב את האלמנטים האלה בשורה, למשל: 1/6, 34/37. שים לב ששברים רגילים כאלה כבר כתובים עם קו נטוי. אחרת, שום דבר לא השתנה באופן משמעותי.
יש גם שברים עשרוניים.הם נוחים לשימוש, אך לא ניתן לייצג מספר כלשהו בצורה זו - לשם כך עליו להיות מתחלק בעשרה ללא שארית, אחרת הדיוק הולך לאיבוד. תראו, ניתן לכתוב ½ בצורה עשרונית, קבלת 0.5 ו- 1/3 כבר לא אפשרי. במקום זאת, אתה מקבל 0.333 ... וכן הלאה. במתמטיקה זה נקרא "שלוש בתקופה".
האם ניתן לכתוב שבר במחשב?"Word" מספק הזדמנות כזו. אתה רק צריך לעבור לקטע "הוסף". שם תראה את כפתור "הנוסחה", כשתלחץ עליו ייפתח חלון חדש. בו תוכלו למצוא גם שברים רגילים וגם סמלים רבים אחרים, מורכבים הרבה יותר - אינטגרלים, דיפרנציאלים, שורשים מרובעים.
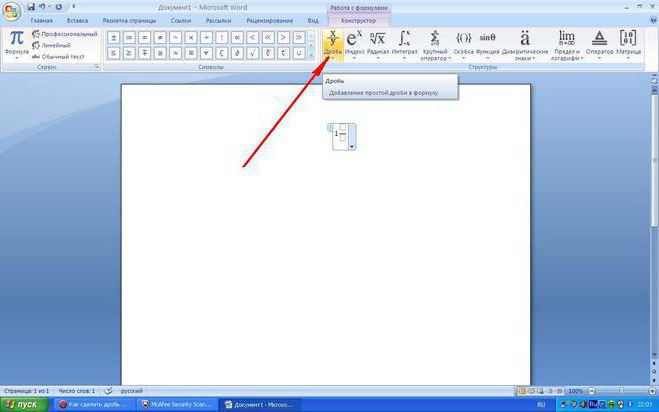
אולי עדיין לא ידעת מילים כאלה, אבל יום אחד במתמטיקה תעבור גם אותן. זכרו כי ניתן למצוא את כל הסימנים הללו במקום אחד.
יחד עם זאת, תכונה זו אינה מסופקת ב- "Notepad". שם, ניתן יהיה לכתוב שברים רק בשורה, דרך קו נטוי.
הדיוק חשוב בכל מדע.לכן יש לקחת בחשבון את כל ה"פיסות "ולשם כך חובה להבין כיצד לעבוד עם שברים נכונים ולא נכונים. בלעדיהם המטוס לא ימריא, והמחשב לא יופעל, ולא תוכלו לבשל מנה מספר בישול, ואפילו לא תוכלו לכתוב מוסיקה. באופן כללי, הבנת נושא זה בשיעורי מתמטיקה היא משימה הכרחית בהחלט, והכי חשוב, זה בכלל לא קשה. תרגול להכין שיעורי בית, להוסיף, להכפיל, להשוות שברים. אז תלמד מהר מאוד כיצד לעשות הכל בראש שלך ותוכל לעבור לנושאים מעניינים חדשים. ותאמין לי, יש עדיין הרבה מאוד כאלה במתמטיקה.


























