
次に、幾何学的光学に焦点を当てます。このセクションでは、レンズなどのオブジェクトに多くの時間を費やします。結局のところ、それは異なる可能性があります。この場合、薄いレンズの式はすべての場合で同じです。あなたはそれを正しく適用する方法を知る必要があるだけです。

それは常に光線を透過する体であり、特別な形をしています。オブジェクトの外観は、2つの球面によって決定されます。それらの1つは平らなものと交換することができます。
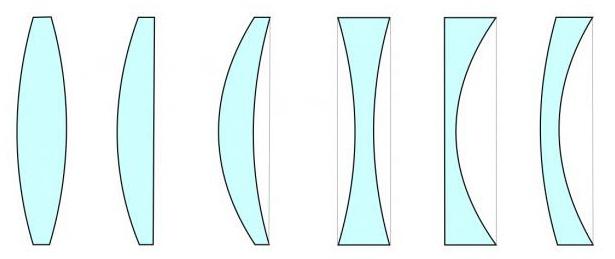
さらに、レンズは中央またはエッジ。前者の場合は凸型、2番目の場合は凹型と呼ばれます。さらに、凹面、凸面、平面の組み合わせ方によって、レンズも異なる場合があります。すなわち:両凸と両凹、平凸と平凸、凸凹と凹凸。
通常の状態では、これらのオブジェクトは空気。それらは、光学密度が空気の光学密度よりも大きい物質から作られています。したがって、凸レンズが集まり、凹レンズが散乱します。
話をする前に 薄いレンズ式、基本的な概念を決定する必要があります。あなたは間違いなくそれらを知る必要があります。彼らは常にさまざまなタスクによって対処されるためです。
主な光軸は直線です。両方の球面の中心を通って描画され、レンズの中心がどこにあるかを定義します。追加の光軸もあります。それらはレンズの中心点を通して描かれますが、球面の中心は含まれていません。
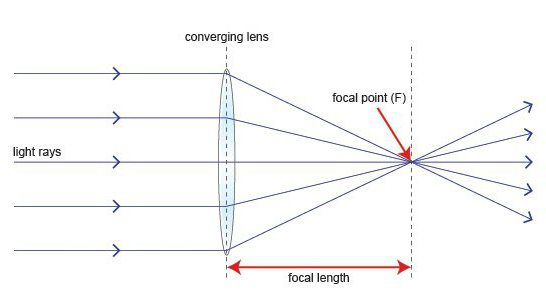
薄いレンズの式には、その焦点長を決定する値があります。したがって、焦点は主光軸上の点です。指定された軸に平行に走る光線と交差します。
さらに、薄いレンズごとに常に2つのトリックがあります。それらはその表面の両側にあります。両方のフォーカスが有効です。散乱するものは架空のものです。
レンズから焦点までの距離が焦点長(文字) F). さらに、その値は正(収集の場合)または負(散乱の場合)になります。
もう1つの特性は、焦点長、つまり光パワーに関連しています。それを示すのが通例です D。 その値は常にフォーカスの逆です。つまり、 D = 1 /F。 光パワーはディオプター(略して、ディオプター)で測定されます。
すでに示された焦点の長さに加えて、いくつかの距離とサイズを知る必要があります。それらはすべてのタイプのレンズで同じであり、表に示されています。
| 記法 | タイトル |
| d | オブジェクトまでの距離 |
| x | 研究対象の身長 |
| f | 画像距離 |
| X | 結果の画像の高さ |
示されたすべての距離と高さは通常、メートル単位で測定されます。
物理学では、拡大の概念は薄いレンズの公式にも関連しています。これは、オブジェクトの高さに対する画像の寸法の比率、つまりH / hとして定義されます。. 文字Gで指定できます。
式を取得するには、これを知る必要があります集めたり拡散したりする薄いレンズ。描画は、両方のレンズが独自の概略図を持っているという事実から始まります。どちらもラインセグメントのように見えます。端に集まるものだけが矢印を外側に向け、散乱するものはこのセグメントの内側に向けます。
今、このセグメントに描画する必要がありますその中央に垂直。これは主な光軸を表します。レンズの両側に同じ距離で、焦点をマークすることになっています。
作成するオブジェクトは矢印の形で描画されます。アイテムの上部がどこにあるかを示します。一般に、オブジェクトはレンズと平行に配置されます。
オブジェクトのイメージを作成するために、画像の両端のポイントを見つけて接続するだけで十分です。これらの2つのポイントはそれぞれ、2つの光線の交点から取得できます。構築するのが最も簡単なのはそのうちの2つです。
メインに平行な指定されたポイントから実行光軸。レンズに接触した後、それはメインフォーカスを通過します。収集レンズについて話している場合、この焦点はレンズの後ろにあり、ビームはレンズを通過します。散乱ビームを考慮する場合、ビームの継続がレンズの前の焦点を通過するようにビームを向ける必要があります。
レンズの光学焦点を直接通過します。彼は彼女の後で方向を変えません。
商品がお届けされる場合がございます主光軸に垂直で、その上で終わります。次に、軸上にない矢印のエッジに対応するポイントのイメージを作成するだけで十分です。そして、そこから軸に垂直線を引きます。これがオブジェクトの画像になります。
構築された点の交点がイメージを与えます。薄い収束レンズで実際の画像が得られます。つまり、光線の交点で直接取得されます。例外は、オブジェクトがレンズとフォーカスの間に配置されている場合(拡大鏡のように)、画像が架空のものであることが判明する場合です。散乱するものの場合、それは常に架空のものであることがわかります。結局のところ、それは光線自体ではなく、それらの延長の交差点で得られます。
実際の画像は実線で描くのが通例です。しかし、架空のものは点在しています。これは、最初のものが実際にそこにあり、2番目のものが見られるだけであるという事実によるものです。
これは、収集レンズでの実際の画像の構成を示す図に基づいて行うと便利です。セグメントの指定は、図に示されています。
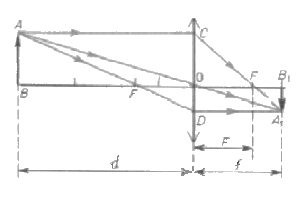
光学セクションは、理由から幾何学的と呼ばれます。数学のこの特定のセクションからの知識が必要になります。まず、三角形AOBとAを考慮する必要があります1OV1..。それらは2つの等しい角度(直線と垂直)を持っているので似ています。それらの類似性から、セグメントAのモジュールは1その1 およびABは、OBセグメントのモジュールを指します1 およびOV。
さらに2つの三角形が類似しています(2つの角度で同じ原理に基づいています)。 COF およびA1Fb1..。それらでは、セグメントのそのようなモジュールの比率は等しい:А1その1 COと Fb1と の。 構造に基づいて、セグメントABとCOは等しくなります。したがって、指定された関係の等式の左側は同じです。したがって、権利も同じです。つまり、OV1 /ОВは等しい Fb1/ の。
この同等性では、ドットで示されるセグメントは、対応する物理的概念で置き換えることができます。だからOV1 レンズから画像までの距離です。 RHは、オブジェクトからレンズまでの距離です。 OF- 焦点距離。セグメント Fb1 画像までの距離と焦点の差に等しい。したがって、別の方法で書き直すことができます。
f / d = (f-F) / F または Ff = df-dF。
薄いレンズの式を導出するには、最後の等式をで割る必要があります dfF。 それからそれは判明します:
1 / d + 1 / f = 1 / F。
このyは薄い収集レンズ式を持っています。発散焦点長は負です。これは平等の変化につながります。確かに、それは重要ではありません。薄い拡散レンズの式では、比率1 /の前にマイナスがあるというだけです。F。 つまり:
1 / d + 1 / f = --1 / F。
状態。 収集レンズの焦点長は0.26mです。物体が30cmの距離にある場合は、倍率を計算する必要があります。
決定。それは、Cでの指定の導入と単位の変換から始める必要があります。だから、知られている d = 30 cm = 0.3mおよび F = 0.26 m。ここで式を選択する必要があります。主なものは拡大用に示されているもので、2番目は薄い収集レンズ用です。
それらはどういうわけか組み合わせる必要があります。これを行うには、収集レンズで画像を作成するための図面を検討する必要があります。このような三角形から、Г= H / hであることがわかります。= f / d。つまり、倍率を見つけるには、オブジェクトまでの距離に対する画像までの距離の比率を計算する必要があります。
2番目は知られています。ただし、画像までの距離は、前述の式から導き出されることになっています。それが判明しました
f = dF /(d - F)。
次に、これら2つの式を組み合わせる必要があります。
Г= dF /(d(d - F))= F /(d - F)。
現時点では、薄いレンズの公式の問題の解決策は基本的な計算に還元されています。既知の値を置き換えることは残っています:
G = 0.26 /(0.3-0.26)= 0.26 / 0.04 = 6.5。
回答:レンズは6.5倍に拡大します。

状態。 ランプは収集レンズから1メートルのところにあります。スパイラルの画像は、レンズから25cm離れたスクリーンで取得されます。指定されたレンズの焦点長を計算します。
決定。 次の値をデータに書き込むことになっています: d = 1mおよび f = 25 cm = 0.25m。この情報は、薄いレンズの式から焦点長を計算するのに十分です。
だから1 /F = 1/1 + 1 / 0.25 = 1 + 4 = 5。ただし、タスクでは、光パワーではなく、焦点を知る必要があります。したがって、1を5で割るだけで、焦点の長さが得られます。
F = 1/5 = 0、2メートル。
回答:収集レンズの焦点長は0.2mです。
状態..。ろうそくは収集レンズから15cmの距離に置かれました。その光パワーは10ディオプターです。レンズの後ろのスクリーンは、キャンドルの鮮明な画像が得られるように配置されています。この距離は何に等しいですか?
決定。 次のデータを短いレコードに書き込むことになっています。 d = 15 cm = 0.15 m、 D = 10ジオプター。上記の式は、少し変更を加えて作成する必要があります。つまり、平等の右側に、 D 1 /の代わりにF。
いくつかの変換の後、レンズから画像までの距離について次の式が得られます。
f = d /(dD - 1)。
次に、すべての数値とカウントを置き換える必要があります。それはそのような値であることがわかります f: 0.3メートル。
回答:レンズからスクリーンまでの距離は0.3mです。

状態。 物体とその画像は11cm離れています。収集レンズは3倍の倍率を提供します。その焦点の長さを見つけます。
決定。 オブジェクトとその画像の間の距離は、文字で簡単に示されます L = 72 cm = 0.72m。倍率G = 3。
ここでは2つの状況が考えられます。1つ目は、被写体がピントの後ろにある、つまり画像がリアルであるということです。第二に、焦点とレンズの間に物体があります。その場合、画像はオブジェクトと同じ側からのものであり、架空のものです。
最初の状況を考えてみましょう。物体と画像は収集レンズの反対側にあります。ここでは、次の式を書くことができます。 L = d + NS。 2番目の方程式は次のように記述されることになっています。Г= f / NS。 これらの方程式のシステムを2つの未知数で解く必要があります。これを行うには、 L 0.72 m、Gは3です。
2番目の式から、次のことがわかります。 f = 3NS。 次に、最初のものは次のように変換されます:0.72 = 4NS。 数えるのは簡単です d = 0、18(メートル)。定義が簡単になりました f = 0.54(m)。
焦点距離を計算するために薄レンズの公式を使用することは残っています。 F =(0.18 * 0.54)/(0.18 + 0.54)= 0.135(m)これが最初のケースの答えです。
2番目の状況では、画像は架空のものであり、 L 異なります: L = f - NS。 システムの2番目の方程式は同じになります。同様に議論すると、 d = 0、36(m)、および f = 1.08(m)。焦点距離を同様に計算すると、次の結果が得られます:0.54(m)。
回答:レンズの焦点距離は0.135mまたは0.54mです。
薄いレンズの光線の経路は重要です幾何光学の実用化。結局のところ、それらは単純な拡大鏡から精密顕微鏡や望遠鏡まで、多くのデバイスで使用されています。したがって、それらについて知る必要があります。
薄いレンズの導出式は、解くことを可能にします多くのタスク。さらに、さまざまなタイプのレンズがどのような画像を提供するかについて結論を出すことができます。この場合、焦点距離と物体までの距離を知るだけで十分です。
