
三角形は最も一般的なものの1つです小学校ですでに知っている幾何学的な形。すべての学生は、ジオメトリのレッスンで三角形の領域を見つける方法の問題に直面しています。だから、与えられた人物の領域を見つけることのどのような特徴を区別することができますか?この記事では、このようなタスクを完了するために必要な基本的な式を確認し、三角形のタイプも分析します。

ジオメトリでは、3つのコーナーを含む複数のタイプの形状が区別されるため、三角形の領域はまったく異なる方法で見つけることができます。これらのタイプは次のとおりです。
既存のタイプの三角形のそれぞれを詳しく見てみましょう。

この幾何学的な図は最も考えられています幾何学的問題を解決するのに一般的です。任意の三角形を描く必要が生じた場合、このオプションが役に立ちます。
鋭角の三角形では、その名前が示すように、すべての角度が鋭角で、合計で180°になります。
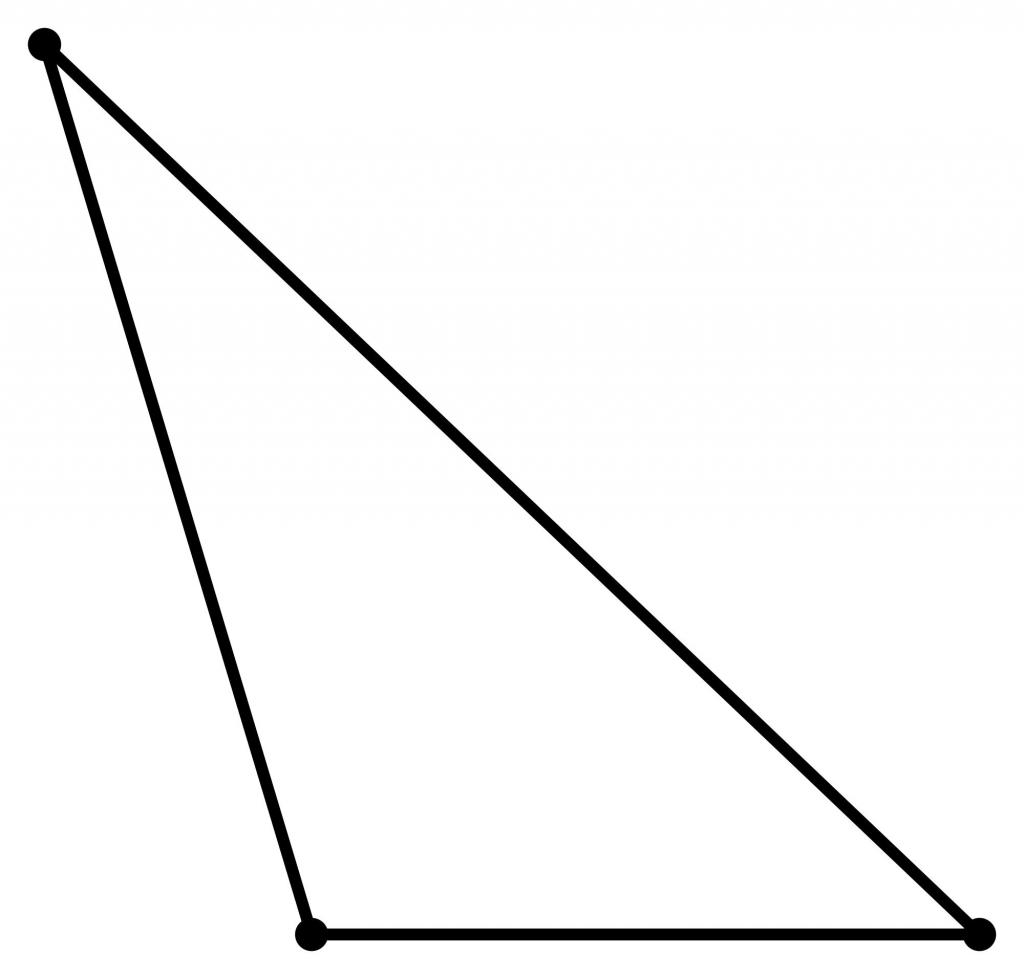
この三角形も非常に一般的です、ただし、それはやや一般的ではありません。たとえば、三角形を解くとき(つまり、その辺と角度のいくつかを知っていて、残りの要素を見つける必要がある)、角度が鈍いかどうかを判断する必要がある場合があります。鈍角の余弦は負の数です。
鈍い三角形では、角度の1つが90°を超えるため、残りの2つの角度は小さな値を取る可能性があります(たとえば、15°または3°)。
このタイプの三角形の領域を見つけるには、いくつかのニュアンスを知る必要があります。これについては、さらに詳しく説明します。
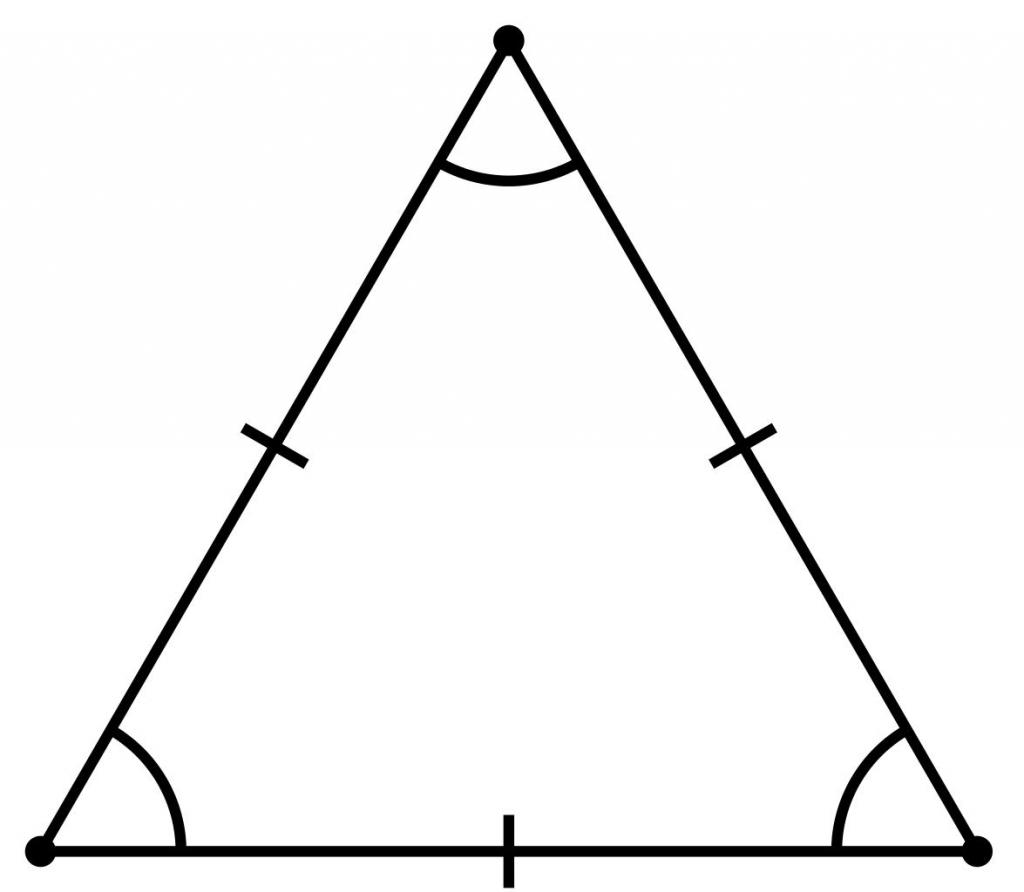
通常のポリゴンは図ですすべての側面と角度が等しいn個のコーナーを含みます。これは通常の三角形です。三角形のすべての角度の合計は180°であるため、3つの角度のそれぞれは60°です。
規則的な三角形は、その特性から、等辺図とも呼ばれます。
また、通常の三角形には1つの円しか刻印できず、その周りに1つの円しか記述できず、それらの中心は1点に配置されていることにも注意してください。

等辺型に加えて、区別することもできますそれとは少し異なる等角三角形。このような三角形では、2つの辺と2つの角度が互いに等しく、3番目の辺(等しい角度が隣接している)がベースになります。
この図は、角度DとFが等しい等速三角形DEFを示しており、DFがベースです。

直角の三角形は、その角度の1つがまっすぐである、つまり90°に等しいため、そのように名付けられています。他の2つの角度は合計で90°になります。
90°の角度の反対側にあるこのような三角形の最大の辺はハイポテヌスであり、他の2つの辺は脚です。このタイプの三角形には、ピタゴリアンの定理が適用されます。
脚の長さの二乗の合計は、下垂体の長さの二乗に等しい。
この図は、低腱ACと脚ABおよびBCを備えた直角三角形BACを示しています。
直角の三角形の領域を見つけるには、その脚の数値を知る必要があります。
この図の領域を見つけるための式に移りましょう。
ジオメトリでは、2つの式を区別できます。ほとんどのタイプの三角形、つまり鋭角、鈍角、規則的、等角の三角形の領域を見つけるのに適しています。それぞれを分析してみましょう。
この式は普遍的です私たちが検討している図の領域を見つける。これを行うには、側面の長さとそれに引き寄せられる高さの長さを知るだけで十分です。式自体(ベースと高さの積の半分)は次のようになります。
S =½* A * H、
ここで、Aはこの三角形の辺、Hは三角形の高さです。

たとえば、鋭角の三角形ACBの領域を見つけるには、その辺ABに高さCDを掛け、結果の値を2で割ります。
ただし、その地域を見つけるのは必ずしも簡単ではありませんこのように三角形。たとえば、この式を鈍い三角形に使用するには、その辺の1つを続けてから、その辺に高さを描画する必要があります。
実際には、この式は他の式よりも頻繁に使用されます。
この式は、前の式と同様に、ほとんどの三角形の、そしてその意味は、三角形の側面と高さで面積を見つけるための式の結果です。つまり、考慮される式は前の式から簡単に導き出すことができます。その文言は次のようになります。
S =½* sinO * A * B、
ここで、AとBは三角形の辺であり、Oは辺AとBの間の角度です。
角度のサインは、優れたソビエト数学者V.M.Bradisにちなんで名付けられた特別なテーブルで見ることができることを思い出してください。
それでは、例外的なタイプの三角形にのみ適した他の式に移りましょう。
三角形に高さを描く必要性を含む普遍的な公式に加えて、直角を含む三角形の領域は、その脚によって見つけることができます。
したがって、直角を含む三角形の面積は、その脚の積の半分、または:
S =½* a * b、
ここで、aとbは右三角形の脚です。
このタイプの幾何学的形状は、その面積は、その辺の1つだけの示された値で見つけることができます(通常の三角形のすべての辺が等しいため)。したがって、「辺が等しいときに三角形の領域を見つける」という問題に直面して、次の式を使用する必要があります:
S = A2*√3/ 4、
ここで、Aは等辺三角形の辺です。
三角形の領域を見つけるための最後のオプションは、ヘロンの式です。それを使用するには、図の3辺の長さを知る必要があります。ヘロンの式は次のようになります。
S =√p(p-a)(p-b)(p-c)、
ここで、a、b、cはこの三角形の辺です。
時々問題が与えられます:「通常の三角形の領域-その辺の長さを見つけてください」。この場合、通常の三角形の領域を見つけるためにすでに知られている式を使用し、そこから辺(またはその正方形)の値を導出する必要があります:
A2 = 4S /√3。
数学におけるGIAの問題には、多くの公式があります。さらに、市松模様の紙で三角形の領域を見つける必要があることがよくあります。
この場合、図の片側に高さを描画し、セルによってその長さを決定し、普遍的な式を使用して領域を見つけるのが最も便利です。
S =½* A * H。
したがって、記事に示されている式を研究した後、どんな種類の三角形の領域を見つけるのにも問題はありません。
