
우주에서 비행기는 다른 방법으로 설정할 수 있습니다.방법 (1 점과 벡터, 2 점과 벡터, 3 점 등). 이를 염두에두고 평면의 방정식은 다양한 형태를 가질 수 있습니다. 또한 특정 조건이 충족되면 평면은 평행, 수직, 교차 등이 될 수 있습니다. 이 기사에서 이에 대해 이야기 할 것입니다. 비행기 등의 일반 방정식을 그리는 방법을 배웁니다.
공백 R이 있다고 가정합니다.3, 직사각형 XYZ 좌표계가 있습니다. 초기 점 O에서 해제 될 벡터 α를 정의 해 보겠습니다. 벡터 α의 끝을 통해 평면 P를 그립니다. 이는 수직이 될 것입니다.
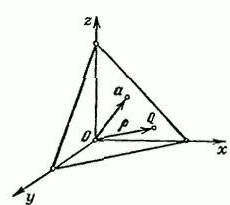
임의의 점 Q = (x, y, z)를 나타냅니다. 점 Q의 반경 벡터를 문자 p로 서명합시다. 이 경우 벡터 α의 길이는 p = IαI 및 Ʋ = (cosα, cosβ, cosγ)와 같습니다.
이것은 다음으로 향하는 단위 벡터입니다.측면뿐만 아니라 벡터 α. α, β 및 γ는 각각 벡터 Ʋ와 공간 축 x, y, z의 양의 방향 사이에 형성되는 각도입니다. 모든 점 QϵП의 벡터 Ʋ에 대한 투영은 상수 값이며 p : (p, Ʋ) = p (p≥0)와 같습니다.
위의 방정식은 p = 0 일 때 의미가 있습니다. 유일한 것은이 경우 평면 P가 원점 인 점 O (α = 0)와 교차하고 점 O에서 방출되는 단위 벡터 Ʋ는 방향에도 불구하고 P에 수직이됩니다. 즉, 벡터 Ʋ는 다음과 같이 정의됩니다. 표지판에 정확합니다. 이전 방정식은 벡터 형식으로 표현 된 평면 P의 방정식입니다. 그러나 좌표에서 그 모양은 다음과 같습니다.

여기서 P는 0보다 크거나 같습니다. 우리는 공간에서 평면의 방정식을 정규 형태로 찾았습니다.
좌표의 방정식에 0이 아닌 숫자를 곱하면 동일한 평면을 정의하는 주어진 방정식과 동등한 방정식을 얻습니다. 다음과 같이 표시됩니다.

여기서 A, B, C는 동시에 0이 아닌 숫자입니다. 이 방정식을 일반 평면 방정식이라고합니다.
일반 형식의 방정식은 추가 조건이있는 경우 수정할 수 있습니다. 그들 중 일부를 고려해 봅시다.
계수 A가 0이라고 가정합니다. 이것은이 평면이 주어진 축 Ox에 평행 함을 의미합니다. 이 경우 방정식의 형태는 Vu + Cz + D = 0으로 변경됩니다.
마찬가지로 방정식의 형식은 다음 조건에서 변경됩니다.
숫자 A, B, C, D가 0과 다른 경우 방정식 (0)의 형식은 다음과 같습니다.
x / a + y / b + z / c = 1,
여기서 a = -D / A, b = -D / B, c = -D / C.
결과적으로 우리는 세그먼트의 평면 방정식을 얻습니다. 이 평면은 좌표 (a, 0,0), Oy-(0, b, 0) 및 Oz-(0,0, c)가있는 지점에서 Ox 축과 교차합니다.

방정식 x / a + y / b + z / c = 1을 고려하면 주어진 좌표계를 기준으로 평면의 위치를 시각적으로 쉽게 표현할 수 있습니다.
평면 P에 대한 법선 벡터 n은이 평면의 일반 방정식, 즉 n (A, B, C)의 계수 인 좌표를 갖습니다.

법선 n의 좌표를 결정하기 위해서는 주어진 평면의 일반 방정식을 아는 것으로 충분합니다.
선분 방정식을 사용할 때x / a + y / b + z / c = 1 형식을 갖습니다. 일반 방정식을 사용할 때 주어진 평면의 법선 벡터 좌표를 적을 수 있습니다 : (1 / a + 1 / b + 1 / c).
노멀 벡터가 도움이된다는 점은 주목할 가치가 있습니다.다양한 문제를 해결합니다. 가장 일반적인 문제는 평면의 직각 성 또는 평 행성을 입증하는 문제, 평면 간의 각도 또는 평면과 선 간의 각도를 찾는 문제입니다.
주어진 평면에 수직 인 0이 아닌 벡터 n을 주어진 평면에 대해 법선 (일반)이라고합니다.
좌표 공간 (직사각형 좌표계)에서 Oxyz가 주어진다고 가정합니다.

법선 n에 수직 인 점 Mₒ을 통과하는 평면에 대한 방정식을 작성해야합니다.
우주에서 임의의 지점을 선택하고M (xy, z)로 표시합니다. 점 M (x, y, z)의 반경 벡터를 r = x * i + y * j + z * k로, 점 Mₒ (xₒ, yₒ, zₒ)-rₒ = xₒ * i + yₒ의 반경 벡터를 지정합니다. * j + zₒ * k. 벡터 МₒМ가 벡터 n에 수직이면 점 M은 주어진 평면에 속합니다. 내적을 사용하여 직교성 조건을 작성해 보겠습니다.
[МₒМ, n] = 0.
МₒМ = r – rₒ이므로 평면의 벡터 방정식은 다음과 같습니다.
[r-rₒ, n] = 0.
이 방정식은 다른 형태를 가질 수 있습니다. 이를 위해 내적의 특성을 사용하고 방정식의 좌변을 변환합니다. [r-rₒ, n] = [r, n]-[rₒ, n]. [rₒ, n]이 c로 표시되면 다음 방정식을 얻습니다. [r, n]-c = 0 또는 [r, n] = c는 평면에 속하는 주어진 점의 반경 벡터의 법선 벡터에 대한 투영의 불변성을 표현합니다.
이제 평면의 벡터 방정식을 쓰는 좌표 형식을 얻을 수 있습니다. [r-rₒ, n] = 0. r – rₒ = (x – xₒ) * i + (y – yₒ) * j + (z – zₒ) * k, n = A * i + B * j + C * k는 다음과 같습니다.

우리는 법선 n에 수직 인 점을 통과하는 평면의 방정식을 가지고 있습니다.
A * (x- xₒ) + B * (y– yₒ) C * (z – zₒ) = 0.
두 개의 임의의 점 M '(x', y ', z') 및 M ″ (x ″, y ″, z ″)와 벡터 a (a ′, a ″, a ‴)를 정의 해 보겠습니다.
이제 우리는 주어진 벡터 a에 평행 한 좌표 (x, y, z)를 가진 모든 점 M뿐만 아니라 기존 점 M ′과 M ″을 통과 할 주어진 평면에 대한 방정식을 그릴 수 있습니다.
또한 벡터 M'M = {x-x ′; y-y ′; zz ′} 및 M ″ M = {x ″ -x ′; y ″ -y ′; z ″ -z ′}는 벡터와 동일 평면 상에 있어야합니다. a = (a ′, a ″, a ‴), 이는 (M'M, M ″ M, a) = 0을 의미합니다.
따라서 우주에서 비행기의 방정식은 다음과 같습니다.
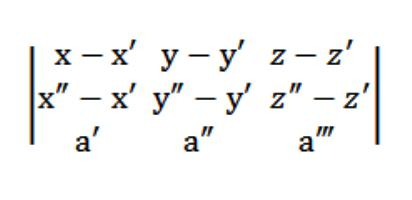
세 가지 점이 있다고 가정 해 봅시다. (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴) 하나의 직선에 속하지 않습니다. 주어진 세 점을 통과하는 평면의 방정식을 쓸 필요가 있습니다. 기하학 이론은 이런 종류의 평면이 실제로 존재한다고 주장하며, 오직 하나 뿐이며 흉내낼 수 없습니다. 이 평면은 점 (x ′, y ′, z ′)과 교차하므로 방정식의 형태는 다음과 같습니다.

여기서 A, B, C는 동시에 0이 아닙니다. 또한 주어진 평면은 (x ″, y ″, z ″) 및 (x ‴, y ‴, z ‴)의 두 점을 더 교차합니다. 이와 관련하여 다음 조건을 충족해야합니다.

이제 우리는 미지수 u, v, w로 동종 방정식 시스템 (선형)을 구성 할 수 있습니다.

우리의 경우 x, y 또는 z는 임의적입니다.식 (1)을 만족하는 점. 방정식 (1)과 방정식 시스템 (2) 및 (3)을 고려하면 위 그림에 표시된 방정식 시스템은 사소하지 않은 벡터 N (A, B, C)에 의해 충족됩니다. 이것이이 시스템의 행렬식이 0 인 이유입니다.
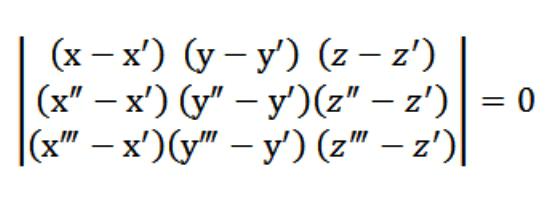
우리가 얻은 방정식 (1)은비행기의 방정식입니다. 3 점을 정확히 통과하며 확인하기 쉽습니다. 이렇게하려면 첫 번째 줄에있는 요소로 행렬식을 확장해야합니다. 행렬식의 기존 속성에서 우리의 평면은 처음에 지정된 세 점 (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴)과 동시에 교차합니다. 즉, 우리는 우리 앞에 놓인 과제를 해결했습니다.
2 면각은하나의 직선에서 나오는 두 개의 반면으로 형성된 공간 기하학적 도형. 즉, 이것은 이러한 반면에 의해 제한되는 공간의 일부입니다.
다음 방정식을 가진 두 개의 평면이 있다고 가정 해 보겠습니다.
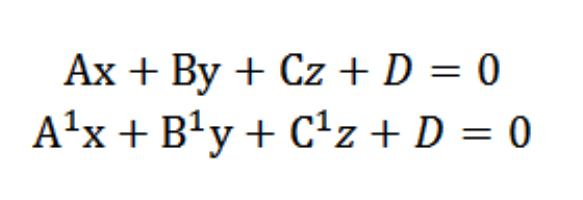
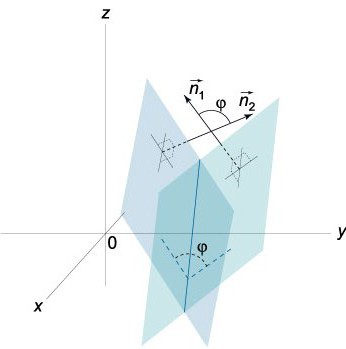
벡터 N = (A, B, C) 및N¹ = (A¹, B¹, C¹)는 주어진 평면에 따라 수직입니다. 이와 관련하여 벡터 N과 N¹ 사이의 각도 φ는 이러한 평면 사이의 각도 (2 면체)와 같습니다. 스칼라 곱은 다음과 같습니다.
NN¹ = | N || N¹ | cos φ,
정확히 왜냐하면
cosφ = NN¹ / | N || N¹ | = (AA¹ + BB¹ + CC¹) / ((√ (A² + B² + C²)) * (√ (A¹) ² + (B¹) ² + (C¹) ²)).
0≤φ≤π를 고려하면 충분합니다.
실제로 교차하는 두 평면은 두 각도 (2 면체)를 형성합니다. φ1 및 φ2... 그들의 합은 π (φ1+ φ2= π). 코사인의 경우 절대 값은 동일하지만 부호가 다릅니다, 즉 cos φ1= -cos φ2... 방정식 (0)에서 A, B 및 C를 각각 숫자 -A, -B 및 -C로 바꾸면 우리가 얻는 방정식은 방정식에서 유일한 각도 φ 인 동일한 평면을 정의합니다 cos φ = NN1/ | N || N1| π-φ로 대체됩니다.
평면은 수직이라고 부릅니다.각도는 90 도입니다. 위에 설명 된 자료를 사용하여 다른 평면에 수직 인 평면의 방정식을 찾을 수 있습니다. Ax + By + Cz + D = 0 및 A¹x + B¹y + C¹z + D = 0이라는 두 개의 평면이 있다고 가정합니다. cosφ = 0이면 수직이라고 주장 할 수 있습니다. 이는 NN¹ = AA¹ + BB¹ + CC¹ = 0을 의미합니다.
평행은 공통점을 포함하지 않는 두 개의 평면입니다.
평면이 평행이되는 조건 (방정식이전 하위 섹션에서와 동일) 벡터 N과 N¹은 이들에 수직 인 벡터가 동일 선상에 있다는 것입니다. 이는 다음 비례 조건이 충족됨을 의미합니다.
A / A¹ = B / B¹ = C / C¹.
비례 조건이 확장되면-A / A¹ = B / B¹ = C / C¹ = DD¹,
이것은이 평면이 일치 함을 나타냅니다. 이것은 방정식 Ax + By + Cz + D = 0 및 A¹x + B¹y + C¹z + D¹ = 0이 하나의 평면을 설명한다는 것을 의미합니다.
주어진 평면 P가 있다고 가정 해 봅시다.방정식 (0). 좌표 (xₒ, yₒ, zₒ) = Qₒ로 점에서 거리를 구해야합니다. 이렇게하려면 평면 P의 방정식을 일반 형식으로 가져와야합니다.
(p, v) = p (p≥0).
이 경우 ρ (x, y, z)는P에 위치한 점 Q의 반경 벡터, p는 영점에서 해제 된 수직 P의 길이이고, v는 방향 a에 위치한 단위 벡터입니다.

P에 속하는 어떤 점 Q = (x, y, z)의 반경 벡터의 차이 ρ-ρº 및 주어진 점 Q의 반경 벡터0= (xₒ, yₒ, zₒ)는 v에 대한 투영의 절대 값이 거리 d와 같은 벡터이며 Q에서 구해야합니다.0= (xₒ, yₒ, zₒ)에서 P :
D = | (ρ-ρ0, v) |,하지만
(ρ-ρ0, v) = (ρ, v)-(ρ0, v) = р– (ρ0, V).
그래서 밝혀졌습니다
d = | (ρ0, v) -p |.
이제 Q에서 거리 d를 계산하는 것을 보았습니다.0 평면 P로, 평면 방정식의 정규 형식을 사용하면서 p의 왼쪽으로 옮기고 x, y, z 대신 마지막에 (xₒ, yₒ, zₒ)를 대체해야합니다.
따라서 결과 표현식의 절대 값, 즉 원하는 d를 찾을 수 있습니다.
매개 변수 언어를 사용하면 다음과 같은 분명한 사실을 알 수 있습니다.
d = | Axₒ + Byₒ + Czₒ | / √ (A² + B² + C²).
주어진 포인트 Q0 원점과 같이 평면 P의 반대편에 있고 벡터 ρ-ρ 사이에 있습니다.0 v는 둔각이므로 다음과 같습니다.
d =-(ρ-ρ0, v) = (ρ0, v) -p> 0.
포인트 Q의 경우0 원점과 함께 P의 같은면에 있으면 생성 된 각도가 예각입니다.
d = (ρ-ρ0, v) = p-(p0, v)> 0.
결과적으로 첫 번째 경우 (ρ0, v)> р, 두 번째 (ρ0, v) <p.
탄젠트 Mº 지점에서 서피스에 대한 탄젠트 평면은 서피스의이 지점을 통해 그려진 커브에 대한 모든 가능한 탄젠트를 포함하는 평면입니다.
이러한 형태의 표면 방정식 F (x, y, z) = 0을 사용하면 접선 점 Mº (xº, yº, zº)에서 접선 평면의 방정식은 다음과 같습니다.
Fx(xº, yº, zº) (x- xº) + Fx(xº, yº, zº) (y- yº) + Fx(xº, yº, zº) (z-zº) = 0.
표면을 명시적인 형식 z = f (x, y)로 설정하면 접선 평면은 다음 방정식으로 설명됩니다.
z-zº = f (xº, yº) (x- xº) + f (xº, yº) (y-yº).
시스템은 3 차원 공간에 있습니다.좌표 (직사각형) Oxyz, 두 평면 P ′ 및 P ″가 주어지고 교차하고 일치하지 않습니다. 직각 좌표계의 평면은 일반 방정식에 의해 결정되기 때문에 P ′ 및 P ″는 방정식 Ax + B'y + C′z + D ′ = 0 및 A ″ x + B ″ y +에 의해 주어진다고 가정합니다. C ″ z + D ″ = 0. 이 경우, 우리는 P ′ 평면의 법선 n ′ (A ′, B ′, C ′)와 P ″ 평면의 법선 n ″ (A ″, B ″, C ″)를가집니다. 평면이 평행하지 않고 일치하지 않기 때문에 이러한 벡터는 동일 선상에 있지 않습니다. 수학 언어를 사용하여이 조건을 다음과 같이 작성할 수 있습니다. n ′ ≠ n ″ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ * C ″), λϵR. P ′와 P ″의 교차점에있는 직선을 문자 a로 표시합니다.이 경우 a = P ′ ∩ P ″입니다.
a는 모든 점의 집합으로 구성된 직선입니다.(공통) 평면 P '및 P ″. 즉, 직선 a에 속하는 모든 점의 좌표는 방정식 A'x + B'y + C'z + D '= 0 및 A ″ x + B ″ y + C ″ z + D ″ = 0을 동시에 충족해야합니다. 이것은 점의 좌표가 다음 방정식 시스템의 특정 솔루션이 될 것임을 의미합니다.

결과적으로 이것의 해결책 (일반)이방정식 시스템은 P '와 P ″의 교차점으로 작용할 직선의 각 점의 좌표를 결정하고 공간의 Oxyz 좌표계 (직사각형)에서 직선 a를 결정합니다.
