
Nå skal vi snakke om geometrisk optikk.I dette avsnittet blir det brukt mye tid på et slikt objekt som en linse. Det kan jo være annerledes. I dette tilfellet er formelen til en tynn linse den samme for alle tilfeller. Du trenger bare å vite hvordan du bruker den riktig.

Det er alltid en kropp som er gjennomsiktig for lysstråler, som har en spesiell form. Utseendet til objektet er diktert av to sfæriske overflater. En av dem kan erstattes med en flat.
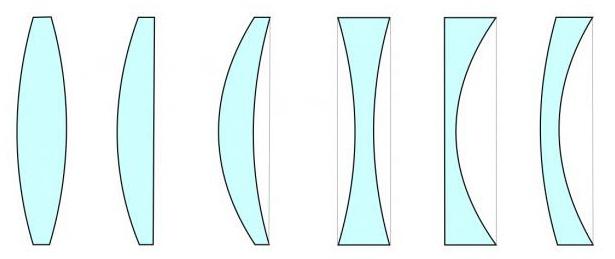
Причем у линзы может оказаться толще середина или kantene. I det første tilfellet vil det bli kalt konveks, i det andre - konkav. Avhengig av hvordan konkave, konvekse og flate overflater er kombinert, kan linsene dessuten være forskjellige. Nemlig: biconvex og biconcave, plano-konveks og plano-konkave, konveks-konkave og konkave-konveks.
Under normale forhold brukes disse gjenstandene ii lufta. De er laget av et stoff hvis optiske tetthet er større enn luften. Derfor vil en konveks linse samles, og en konkav linse vil være spredt.
Før du snakker om tynn linseformel, må du bestemme deg for de grunnleggende konseptene. De må være kjent. Siden de hele tiden vil bli adressert av forskjellige oppgaver.
Главная оптическая ось — это прямая.Den trekkes gjennom sentrene på begge sfæriske overflater og bestemmer plasseringen av linsens sentrum. Det er flere optiske akser. De trekkes gjennom et punkt som er midten av linsen, men inneholder ikke sentrene til sfæriske overflater.
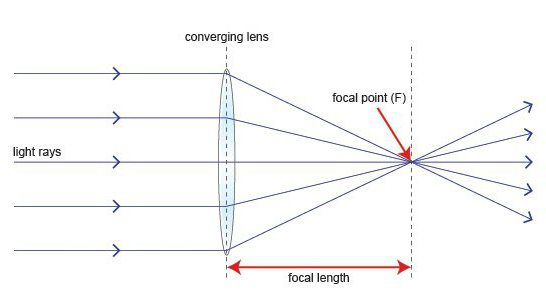
I formelen til en tynn linse er det en mengde som bestemmer brennvidden. Så, fokuset er et punkt på den viktigste optiske aksen. I den krysser stråler som krysser parallelt med den spesifiserte aksen.
Dessuten er det alltid to triks for hver tynne linse. De er plassert på begge sider av overflatene. Begge fokusene på samleren er gyldige. I spredning - innbilt.
Avstanden fra linsen til brennpunktet er brennvidden (bokstav F). Dessuten kan verdien av den være positiv (i tilfelle samling) eller negativ (for spredning).
En annen egenskap er assosiert med brennvidde - optisk kraft. Det er vanlig å betegne D. Verdien er alltid gjensidig med fokus, dvs. D = 1 /F. Målt optisk effekt i dioptre (forkortede dioptre).
I tillegg til den allerede spesifiserte brennvidden, må du vite flere avstander og størrelser. For alle typer linser er de like og presenteres i tabellen.
| betegnelse | navn |
| d | avstand til emne |
| x | høyden på det studerte faget |
| f | avstand til bilde |
| X | høyden på det resulterende bildet |
Alle angitte avstander og høyder måles vanligvis i meter.
I fysikk er forestillingen om forstørrelse også assosiert med formelen til en tynn linse. Det er definert som forholdet mellom størrelsen på bildet og høyden til motivet, dvs. H / h. Det kan betegnes med bokstaven G.
Du må vite dette for å få formelentynn linse, samler eller sprer. Tegningen begynner med at begge linsene har et eget skjematisk bilde. Begge ser ut som et snitt. Bare i samlingen i endene er pilene rettet utover, og i spredningen - innover i dette segmentet.
Nå er det nødvendig å trekke til dette segmentetvinkelrett på midten. Dette viser den optiske hovedaksen. På den, på begge sider av linsen i samme avstand, er det ment å merke triks.
Objektet hvis bilde du vil bygge tegnes i form av en pil. Den viser hvor toppen av varen er. Generelt sett plasseres et objekt parallelt med linsen.
For å bygge et bilde av et objekt,bare finn punktene på endene av bildet, og koble dem deretter. Hvert av disse to punktene kan være et resultat av skjæringspunktet mellom to stråler. De enkleste å bygge er to av dem.
Kommer fra det spesifiserte punktet parallelt med hovedledningenoptisk akse. Etter kontakt med linsen går han gjennom hovedfokuset. Hvis vi snakker om et samleobjektiv, så er dette fokuset bak linsen og strålen går gjennom det. Når spredning vurderes, må strålen tegnes slik at dens fortsettelse passerer gjennom fokuset foran linsen.
Går direkte gjennom det optiske sentrum av linsen. Han endrer ikke retning etter henne.
Det er situasjoner når en vare blir levertvinkelrett på den optiske hovedaksen og ender på den. Da er det nok å bygge et bilde av et punkt som tilsvarer pilens kant, ikke ligger på aksen. Og tegne deretter en vinkelrett på aksen. Dette vil være bildet av motivet.
Skjæringspunktet mellom de konstruerte punktene gir et bilde.I et tynt samleobjektiv oppnås et ekte bilde. Det vil si at den oppnås direkte i krysset mellom strålene. Et unntak er situasjonen når motivet er plassert mellom linsen og fokuset (som i et forstørrelsesglass), da viser bildet seg å være innbilt. Ved spredning viser det seg alltid å være innbilt. Tross alt oppnås det i krysset ikke av strålene selv, men av deres forlengelser.
Selve bildet tegnes vanligvis med en solid linje. Men den imaginære - prikkede linjen. Dette skyldes det faktum at den første faktisk er til stede der, og den andre bare blir sett.
Dette gjøres enkelt på grunnlag av en tegning som illustrerer konstruksjonen av et ekte bilde i et samleobjektiv. Betegnelsen på segmentene er angitt på tegningen.
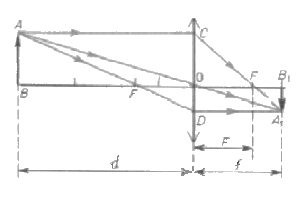
Optikkdelen er ikke forgjeves kalt geometrisk. Det vil ta kunnskap fra denne delen av matematikk. Først må du vurdere trekantene AOW og A1OV1. De er like, fordi de har to like vinkler (rett og vertikal). Av deres likhet følger det at modulene til segmentene A1den1 og AB refererer til som moduler for segmentene til OB1 og OB.
Tilsvarende (basert på samme prinsipp i to vinkler) er to trekanter til: COF og A1Fb1. I dem er forholdene til slike moduler av segmenter like: A1den1 med CO og Fb1med AV. Basert på konstruksjonen, vil segmentene AB og CO være like. Derfor er venstresidene av de angitte likhetene i forhold de samme. Derfor er rettighetene like. Det vil si OB1 / S tilsvarer Fb1/ AV.
I den indikerte likheten kan segmentene indikert med prikker erstattes av de tilsvarende fysiske konseptene. Så ov1 Er avstanden fra linsen til bildet. OB er avstanden fra motivet til linsen. AV - brennvidde. Et segment Fb1 lik forskjellen i avstand til bilde og fokus. Derfor kan det skrives om på en annen måte:
f / d = (f - F) / F eller Ff = df - dF.
For å utlede den tynne linseformelen, må den siste likheten deles inn DFF. Så viser det seg:
1 / d + 1 / f = 1 / F.
Denne har formelen til et tynt samleobjektiv.En spredningsbrennvidde er negativ. Dette fører til en endring i likestilling. Det er sant at det er ubetydelig. Bare i formelen til et tynt spredningsobjektiv er det et minus før forholdet 1 /F. Dvs:
1 / d + 1 / f = - 1 / F.
Betingelse. Brennvidden til samleobjektivet er 0,26 m. Det kreves å beregne økningen hvis motivet er i en avstand på 30 cm.
Beslutning. Det starter med innføring av notasjon og oversettelse av enheter i C. Velkjente d = 30 cm = 0,3 m og F = 0,26 m. Nå må du velge formelen, den viktigste som er indikert for utvidelse, den andre - for et tynt samleobjektiv.
De må på en eller annen måte kombineres. For å gjøre dette, må du vurdere tegningen av bildekonstruksjonen i samleobjektivet. Fra disse trekantene er det tydelig at Γ = H / h= f / d. Det vil si at for å finne forstørrelsen, må du beregne forholdet mellom avstanden og bildet til avstanden til objektet.
Det andre er kjent. Men avstanden til bildet antas å være avledet fra formelen som er angitt tidligere. Viser seg det
f = df / (d - F).
Nå må disse to formlene kombineres.
Г = df / (d(d - F)) = F / (d - F).
For øyeblikket er løsningen på problemet for den tynne linseformelen redusert til elementære beregninger. Det gjenstår å erstatte de kjente verdiene:
G = 0,26 / (0,3 - 0,26) = 0,26 / 0,04 = 6,5.
Svar: linsen gir en forstørrelse på 6,5 ganger.

Betingelse. Lampen er plassert en meter fra samleobjektivet. Bildet av spiralen oppnås på en skjerm 25 cm fra linsen. Beregn brennvidden til den spesifiserte linsen.
Beslutning. Det er ment å skrive følgende verdier i dataene: d = 1 m og f = 25 cm = 0,25 m. Denne informasjonen er tilstrekkelig til å beregne brennvidden fra formelen for en tynn linse.
Altså 1 /F = 1/1 + 1 / 0.25 = 1 + 4 = 5. Men oppgaven krever å kjenne til fokuset, ikke den optiske kraften. Derfor gjenstår det bare å dele 1 med 5, og du får brennvidden:
F = 1/5 = 0,2 m
Svar: Brennvidden til samleobjektivet er 0,2 m.
Betingelse... Stearinlyset ble plassert i en avstand på 15 cm fra samleobjektivet. Den optiske kraften er 10 dioptre. Skjermen bak linsen er plassert slik at man får et klart bilde av stearinlyset på det. Hva er denne avstanden lik?
Beslutning. Det er ment å skrive følgende data i en kort post: d = 15 cm = 0,15 m, D = 10 dioptre. Formelen vist over bør skrives med en liten endring. Nemlig på høyresiden av likestillingen D i stedet for 1 /F.
Etter flere transformasjoner oppnås følgende formel for avstanden fra linsen til bildet:
f = d / (dD - 1).
Nå må du erstatte alle tallene og telle. Det viser seg en slik verdi for f: 0,3 m.
Svar: Avstanden fra linsen til skjermen er 0,3 m.

Betingelse. Objektet og bildet er skilt fra hverandre med 11 cm. Samleobjektivet gir en forstørrelse på 3 ganger. Finn brennvidden.
Beslutning. Avstanden mellom objektet og dets bilde er praktisk angitt med en bokstav L = 72 cm = 0,72 m. Forstørrelse G = 3.
To situasjoner er mulig her.Den første er at motivet ligger bak fokuset, det vil si at bildet er ekte. I det andre er det et objekt mellom fokus og linsen. Da er bildet fra samme side som objektet, og det er imaginært.
La oss vurdere den første situasjonen. Objektet og bildet er på motsatte sider av samleobjektivet. Her kan du skrive følgende formel: L = d + f. Den andre ligningen skal være skrevet: Г = f / d. Det er nødvendig å løse systemet med disse ligningene med to ukjente. For å gjøre dette, bytt ut L med 0,72 m og G med 3.
Fra den andre ligningen viser det seg at f = 3d. Så blir den første transformert slik: 0,72 = 4d. Det er lett å telle fra det d = 0,18 (m). Det er nå lett å definere f = 0,54 (m).
Det gjenstår å bruke den tynne linseformelen for å beregne brennvidden. F = (0,18 * 0,54) / (0,18 + 0,54) = 0,135 (m). Dette er svaret for den første saken.
I den andre situasjonen er bildet imaginært, og formelen for L vil være annerledes: L = f - d. Den andre ligningen for systemet vil være den samme. Argumenterer på samme måte, finner vi det d = 0,36 (m), og f = 1,08 (m). En lignende beregning av brennvidden vil gi følgende resultat: 0,54 (m).
Svar: Brennvidden på linsen er 0.135 m eller 0.54 m.
Banen til stråler i en tynn linse er viktigpraktisk anvendelse av geometrisk optikk. Tross alt brukes de i mange enheter, fra enkle forstørrelsesglass til presisjonsmikroskoper og teleskoper. Derfor er det nødvendig å vite om dem.
Den avledede formelen til en tynn linse gjør det mulig å løsemange oppgaver. Videre lar den deg trekke konklusjoner om hvilket bilde forskjellige typer linser gir. I dette tilfellet er det nok å vite brennvidde og avstand til objektet.


























