Jak znaleźć minimalne i maksymalne punkty funkcji: cechy, metody i przykłady

Функция и исследование ее особенностей занимает jeden z kluczowych rozdziałów współczesnej matematyki. Głównym składnikiem dowolnej funkcji są wykresy przedstawiające nie tylko jej właściwości, ale także parametry pochodnej tej funkcji. Spójrzmy na ten trudny temat. Więc jaki jest najlepszy sposób na wyszukiwanie maksymalnych i minimalnych punktów funkcji?

Funkcja: definicja

Każda zmienna, która w jakiś sposób zależy od wartości innej wielkości, może być nazwana funkcją. Na przykład funkcja f (x²) jest kwadratowy i określa wartości dla całego zestawu x. Załóżmy, że x = 9, wówczas wartość naszej funkcji będzie wynosić 9²= 81

Funkcje mają wiele różnych form:logiczne, wektorowe, logarytmiczne, trygonometryczne, numeryczne i inne. W ich badania zaangażowane były takie wybitne umysły, jak Lacroix, Lagrange, Leibniz i Bernoulli. Ich pisma służą jako bastion we współczesnych sposobach badania funkcji. Przed znalezieniem punktów minimalnych bardzo ważne jest zrozumienie samego znaczenia funkcji i jej pochodnej.

Pochodna i jej rola

Wszystkie funkcje zależą od ichzmienne, co oznacza, że ​​w każdej chwili mogą zmienić swoją wartość. Na wykresie zostanie to przedstawione jako krzywa opadająca lub wznosząca się wzdłuż osi rzędnych (jest to cały zestaw liczb „y” wzdłuż pionu wykresu). Czyli określenie punktu maksimum i minimum funkcji jest właśnie związane z tymi „fluktuacjami”. Wyjaśnijmy, czym jest ten związek.

Na wykresie pokazana jest pochodna dowolnej funkcjiw celu zbadania jej głównych cech i obliczenia szybkości zmiany funkcji (tj. zmiany jej wartości w zależności od zmiennej „x”). W momencie wzrostu funkcji wykres jej pochodnej również się zwiększy, ale w każdej sekundzie funkcja może zacząć maleć, a następnie wykres pochodnej będzie się zmniejszał. Punkty, w których pochodna przechodzi od znaku minus do plusa, nazywane są punktami minimalnymi. Aby wiedzieć, jak znaleźć punkty minimalne, należy lepiej zrozumieć pojęcie pochodnej.

Jak obliczyć pochodną?

Definiowanie i obliczanie pochodnej funkcjiimplikuje kilka pojęć z rachunku różniczkowego. Generalnie samą definicję pochodnej można wyrazić w następujący sposób: jest to wielkość, która pokazuje tempo zmian funkcji.

Matematyczny sposób określenia tego dla wieluwydaje się to trudne dla uczniów, ale w rzeczywistości wszystko jest znacznie prostsze. Wystarczy postępować zgodnie ze standardowym planem znajdowania pochodnej dowolnej funkcji. Poniżej opisano, w jaki sposób można znaleźć punkt minimalny funkcji bez stosowania zasad różniczkowania i bez zapamiętywania tabeli pochodnych.

1. Możesz obliczyć pochodną funkcji za pomocągrafika. Aby to zrobić, musisz przedstawić samą funkcję, a następnie wziąć jeden punkt (punkt A na rysunku). Narysuj linię pionowo w dół do osi odciętych (punkt x₀), aw punkcie A narysuj styczną do wykresuFunkcje. Oś odciętych i linia styczna tworzą pewien kąt a. Aby obliczyć wartość, jak szybko funkcja rośnie, konieczne jest obliczenie stycznej tego kąta a.
2. Okazuje się, że styczna kąta między styczną akierunek osi x jest pochodną funkcji w małym przekroju z punktem A. Metoda ta jest uważana za geometryczny sposób wyznaczania pochodnej.

Metody badań funkcji

W szkolnym programie nauczania matematyki jest to możliweznalezienie minimalnego punktu funkcji na dwa sposoby. Pierwszą metodę przeanalizowaliśmy już za pomocą wykresu, ale jak określić liczbową wartość pochodnej? Aby to zrobić, będziesz musiał nauczyć się kilku formuł, które opisują właściwości pochodnej i pomagają konwertować zmienne, takie jak „x”, na liczby. Poniższa metoda jest uniwersalna, więc można ją zastosować do prawie wszystkich rodzajów funkcji (zarówno geometrycznych, jak i logarytmicznych).

1. Konieczne jest zrównanie funkcji z funkcją pochodną, ​​a następnie uproszczenie wyrażenia za pomocą zasad różniczkowania.
2. W niektórych przypadkach, gdy podana jest funkcja, wgdzie zmienna „x” znajduje się w dzielniku, należy określić zakres dopuszczalnych wartości, wyłączając z niej punkt „0” (z tego prostego powodu, że w matematyce w żadnym wypadku nie da się podzielić przez zero).
3. Następnie należy przekształcić pierwotną postać funkcji w proste równanie, zrównując całe wyrażenie z wartością zero. Na przykład, jeśli funkcja wyglądałaby tak: f (x) = 2x³+ 38x, to zgodnie z regułami różniczkowania jego pochodna wynosi f "(x) = 3x²+1. Następnie przekształcamy to wyrażenie w równanie o następującej postaci: 3x²+1 = 0.
4. Po rozwiązaniu równania i znalezieniu punktów „x”,konieczne jest przedstawienie ich na osi odciętych i określenie, czy pochodna w tych obszarach między zaznaczonymi punktami jest dodatnia czy ujemna. Po wyznaczeniu stanie się jasne, w którym momencie funkcja zaczyna się zmniejszać, to znaczy zmienia swój znak z minus na przeciwny. W ten sposób możesz znaleźć zarówno punkty minimalne, jak i maksymalne.

Zasady różnicowania

Najbardziej podstawowy element uczenia się funkcji ijego pochodną jest znajomość zasad różnicowania. Tylko z ich pomocą można przekształcić nieporęczne wyrażenia i duże złożone funkcje. Zapoznajmy się z nimi, jest ich sporo, ale wszystkie są bardzo proste ze względu na naturalne właściwości funkcji potęgowych i logarytmicznych.

1. Pochodna dowolnej stałej wynosi zero (f (x) = 0). Oznacza to, że pochodna f (x) = x⁵+ x - 160 będzie wyglądać następująco: f "(x) = 5x⁴+1.
2. Pochodna sumy dwóch wyrazów: (f + w) "= f" w + fw ".
3. Pochodna funkcji logarytmicznej: (log_ad) "= d / ln a * d. Ten wzór ma zastosowanie do wszystkich rodzajów logarytmów.
4. Potęga pochodna: (x^Pan) "= n * x^n-1... Na przykład (9x²) "= 9 * 2x = 18x.
5. Pochodna funkcji sinusoidalnej: (sin a) "= cos a. Jeżeli grzech kąta a wynosi 0,5, to jego pochodna wynosi √3 / 2.

Punkty skrajne

Wymyśliliśmy już, jak znaleźć minimalne punkty,jednak istnieje również koncepcja punktów maksymalnych funkcji. Jeżeli minimum oznacza punkty, w których funkcja przechodzi od znaku minus do plusa, to punkty maksymalne to te punkty na osi odciętych, w których pochodna funkcji zmienia się z plusa na przeciwny - minus.

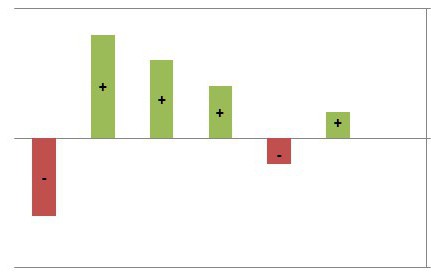
Możliwe jest znalezienie punktów maksymalnych zgodnie z metodą opisaną powyżej, należy tylko wziąć pod uwagę, że wyznaczają one te odcinki, w których funkcja zaczyna się zmniejszać, to znaczy pochodna będzie mniejsza od zera.

W matematyce zwykle uogólnia się oba pojęcia,zastępując je wyrażeniem „skrajne punkty”. Gdy zadanie wymaga określenia tych punktów, oznacza to, że konieczne jest obliczenie pochodnej tej funkcji i znalezienie punktów minimalnej i maksymalnej.