
У свемиру авион се може поставити различитимначина (једна тачка и вектор, две тачке и вектор, три тачке итд.). Имајући то у виду, једначина равни може имати различите облике. Такође, ако су испуњени одређени услови, равни могу бити паралелне, окомите, укрштене итд. О овоме ћемо говорити у овом чланку. Научићемо како саставити општу једначину равни и још много тога.
Претпоставимо да постоји размак Р.3, који има правоугаони КСИЗ координатни систем. Дефинирајмо вектор α, који ће се ослободити из почетне тачке О. Кроз крај вектора α, нацртати раван П, која ће бити на њу окомита.
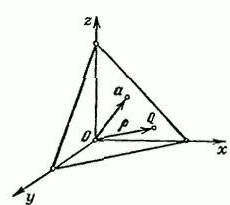
Означавамо на произвољној тачки К = (к, и, з). Потпишемо радијус вектора тачке К словом п. У овом случају, дужина вектора α једнака је п = ИαИ и Ʋ = (цосα, цосβ, цосγ).
Ово је јединични вектор на који је усмеренострану, као и вектор α. α, β и γ су углови који се формирају између вектора Ʋ и позитивних праваца просторних оса к, и, з. Пројекција било које тачке КϵП на вектор Ʋ је константна вредност, која је једнака п: (п, Ʋ) = п (п≥0).
Горња једначина има смисла када је п = 0.Једино што ће раван П у овом случају пресецати тачку О (α = 0), која је исходиште, а јединични вектор Ʋ емитован из тачке О биће окомит на П, упркос свом смеру, што значи да вектор Ʋ се одређује са тачним знаком. Претходна једначина је једначина наше равни П, изражена у векторском облику. Али у координатама ће његов изглед бити овакав:

П овде је веће или једнако 0. Нашли смо једначину равни у простору у нормалном облику.
Ако се једначина у координатама помножи са било којим бројем који није нула, добијамо једначину еквивалентну датој која дефинише исту раван. То ће изгледати овако:

Овде су А, Б, Ц бројеви који су истовремено различити од нуле. Ова једначина се назива општа једначина равни.
Општа једначина се може модификовати у присуству додатних услова. Хајде да погледамо неке од њих.
Претпоставимо да је коефицијент А једнак 0. То значи да је ова раван паралелна датој оси Ок. У овом случају ће се облик једначине променити: Ву + Цз + Д = 0.
Слично, облик једначине ће се променити под следећим условима:
У случају када су бројеви А, Б, Ц, Д различити од нуле, облик једначине (0) може бити следећи:
к / а + и / б + з / ц = 1,
где је а = -Д / А, б = -Д / Б, ц = -Д / Ц.
Као резултат тога, добијамо једначину равни у сегментима. Вреди напоменути да ће ова раван пресецати Ок осу у тачки са координатама (а, 0,0), Ои - (0, б, 0) и Оз - (0,0, ц).

Узимајући у обзир једначину к / а + и / б + з / ц = 1, лако је визуелно приказати локацију равни у односу на дати координатни систем.
Вектор нормале н на раван П има координате које су коефицијенти опште једначине ове равни, односно н (А, Б, Ц).

Да би се одредиле координате нормале н, довољно је познавати општу једначину дате равни.
Када се користи једначина сегмента праве којаима облик к / а + и / б + з / ц = 1, пошто при коришћењу опште једначине можете записати координате било ког нормалног вектора дате равни: (1 / а + 1 / б + 1 / ц).
Вреди напоменути да нормални вектор помажерешава разне проблеме. Најчешћи проблеми укључују проблем доказивања окомитости или паралелности равни, проблем проналажења углова између равни или углова између равни и линија.
Вектор н нула н окомит на дату раван назива се нормалан (нормалан) за дату раван.
Претпоставимо да су у координатном простору (правоугаони координатни систем) дати Окиз:

Потребно је саставити једначину за раван која ће проћи кроз тачку Мₒ окомито на нормалу н.
У простору изаберите било коју произвољну тачку иозначавамо га са М (ки, з). Нека је радијус вектора било које тачке М (к, и, з) р = к * и + и * ј + з * к, а радијус вектора тачке Мₒ (кₒ, иₒ, зₒ) - рₒ = кₒ * и + иₒ * ј + зₒ * к. Тачка М ће припадати датој равни ако је вектор МₒМ окомит на вектор н. Написимо услов ортогоналности користећи тачкасти производ:
[ММ, н] = 0.
Пошто је МₒМ = р - рₒ, векторска једначина равни ће изгледати овако:
[р - рₒ, н] = 0.
Ова једначина може имати други облик.За ово се користе својства тачкастог производа, а лева страна једначине се трансформише. [р - рₒ, н] = [р, н] - [рₒ, н]. Ако се [рₒ, н] означи као ц, тада добијамо следећу једначину: [р, н] - ц = 0 или [р, н] = ц, која изражава постојаност пројекција на вектор нормалних полупречника вектора дате тачке које припадају равни.
Сада можете добити координатни облик писања векторске једначине наше равни [р - рₒ, н] = 0. Пошто је р - рₒ = (к - кₒ) * и + (и - иₒ) * ј + (з - зₒ ) * к, и н = А * и + Б * ј + Ц * к, имамо:

Испоставило се да имамо једначину равни која пролази кроз тачку окомиту на нормалу н:
А * (к- кₒ) + Б * (и– иₒ) Ц * (з- зₒ) = 0.
Поставимо две произвољне тачке М ′ (к ′, и ′, з ′) и М ″ (к ″, и ″, з ″), као и вектор а (а ′, а ″, а).
Сада ћемо моћи да направимо једначину дате равни која ће пролазити кроз постојеће тачке М ′ и М ″, као и било коју тачку М са координатама (к, и, з) паралелним са датим вектором а.
Штавише, вектори М′М = {к -к ′; и -и ′; зз ′} и М ″ М = {к ″ -к ′; и ″ -и ′; з ″ -з ′} морају бити копланарни са вектором а = (а ′, а ″, а ‴), што значи да је (М′М, М ″ М, а) = 0.
Дакле, наша једначина равни у свемиру ће изгледати овако:
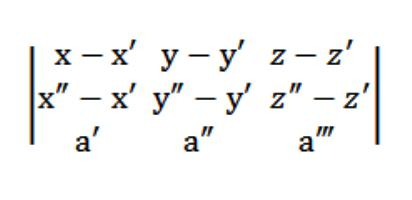
Рецимо да имамо три тачке:(к ′, и ′, з ′), (к ″, и ″, з ″), (к, и ‴, з ‴) које не припадају једној правој. Потребно је написати једначину равни која пролази кроз дате три тачке. Теорија геометрије тврди да ова врста равни заиста постоји, али само је она једина и непоновљива. Пошто ова раван пресеца тачку (к ′, и ′, з ′), облик њене једначине биће следећи:

Овде су А, Б, Ц истовремено различити од нуле. Такође, дата раван пресеца још две тачке: (к ″, и ″, з ″) и (к ‴, и ‴, з ‴). С тим у вези, морају бити испуњени следећи услови:

Сада можемо саставити хомоген систем једначина (линеарних) са непознатим у, в, в:

У нашем случају, к, и или з су произвољнитачка која задовољава једначину (1). Узимајући у обзир једначину (1) и систем једначина (2) и (3), систем једначина наведених на горњој слици задовољен је вектором Н (А, Б, Ц), који је нетривијалан. Зато је одредница овог система једнака нули.
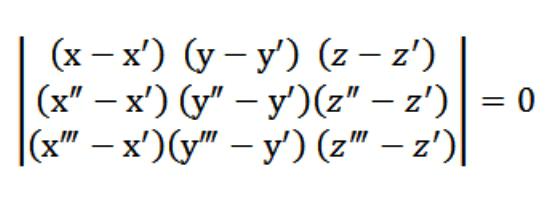
Једначина (1) коју смо добили јеје једначина равни. Пролази тачно кроз 3 тачке и лако се проверава. Да бисмо то урадили, морамо проширити нашу одредницу елементима који се налазе у првом реду. Из постојећих својстава одреднице следи да наша раван истовремено пресеца три почетно одређене тачке (к ′, и ′, з ′), (к ″, и ″, з ″), (к ‴, и ‴, з ‴) . То јест, решили смо задатак који је пред нама.
Двострани угао јепросторна геометријска фигура коју чине две полуравнине које извиру из једне праве линије. Другим речима, ово је део простора који је ограничен овим полуравнима.
Рецимо да имамо две равни са следећим једначинама:
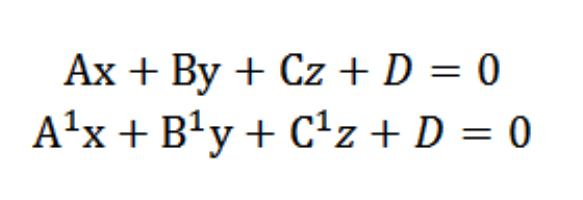
Знамо да су вектори Н = (А, Б, Ц) иН¹ = (А¹, Б¹, Ц¹) су окомите према датим равнинама. С тим у вези, угао φ између вектора Н и Н¹ једнак је углу (двострани) који се налази између ових равни. Тачкасти производ је:
НН¹ = | Н || Н¹ | цос φ,
управо зато
цосφ = НН¹ / | Н || Н¹ | = (АА¹ + ББ¹ + ЦЦ¹) / ((√ (А² + Б² + Ц²)) * (√ (А¹) ² + (Б¹) ² + (Ц¹) ²)).
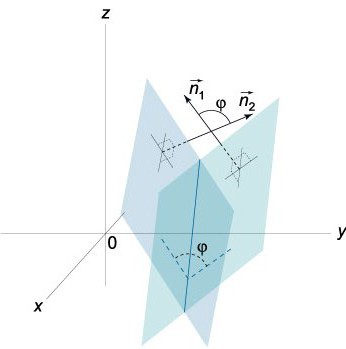
Довољно је узети у обзир да је 0≤φ≤π.
У ствари, две равни које се пресецају формирају два угла (двострани): φ1 и φ2... Њихов збир једнак је π (φ1+ φ2= π). Што се тиче њихових косинуса, њихове апсолутне вредности су једнаке, али се разликују по предзнацима, односно цос φ1= -цос φ2... Ако у једначини (0) заменимо А, Б и Ц бројевима -А, -Б и -Ц, тада ће једначина коју добијемо одредити исту раван, једини угао φ у једначини цос φ = НН1/ | Н || Н1| биће замењен са π-φ.
Авиони се називају окомити, измеђучији је угао 90 степени. Користећи горе наведени материјал, можемо пронаћи једначину равни која је окомита на другу. Претпоставимо да имамо две равни: Ак + Би + Цз + Д = 0 и А¹к + Б¹и + Ц¹з + Д = 0. Можемо тврдити да ће бити окомите ако је цосφ = 0. То значи да је НН¹ = АА¹ + ББ¹ + ЦЦ¹ = 0.
Паралелне су две равни које не садрже заједничке тачке.
Услов да равни буду паралелне (њихове једначинеисто као у претходном одељку) је да су вектори Н и Н¹, који су на њих окомити, колинеарни. То значи да су испуњени следећи услови пропорционалности:
А / А¹ = Б / Б¹ = Ц / Ц¹.
Ако су услови пропорционалности продужени - А / А¹ = Б / Б¹ = Ц / Ц¹ = ДД¹,
ово указује на то да се ове равни подударају. А то значи да једначине Ак + Би + Цз + Д = 0 и А¹к + Б¹и + Ц¹з + Д¹ = 0 описују једну раван.
Рецимо да имамо равнину П која је датаједначина (0). Потребно је пронаћи удаљеност до ње од тачке са координатама (кₒ, иₒ, зₒ) = Кₒ. Да бисте то урадили, морате једначину равни П довести у нормалан облик:
(п, в) = п (п≥0).
У овом случају, ρ (к, и, з) јерадијус вектора наше тачке К, који се налази на П, п је дужина окомице П, која је ослобођена од нулте тачке, в је јединични вектор, који се налази у правцу а.

Разлика ρ-ρº радијусног вектора неке тачке К = (к, и, з), која припада П, као и радијусног вектора дате тачке К0= (кₒ, иₒ, зₒ) је такав вектор, чија је апсолутна вредност пројекције на в једнака удаљености д, која се мора пронаћи из К0= (кₒ, иₒ, зₒ) у П:
Д = | (ρ-ρ0, в) |, али
(ρ-ρ0, в) = (ρ, в) - (ρ0, в) = р– (ρ0, в).
Тако се испоставља
д = | (ρ0, в) -п |.
Сада се види да се израчуна удаљеност д од К0 на раван П, морате користити нормални облик једначине равни, при чему прелазите на леву страну п и замењујете (кₒ, иₒ, зₒ) у последњој уместо к, и, з.
Тако ћемо пронаћи апсолутну вредност резултујућег израза, односно жељени д.
Користећи језик параметара, добијамо очигледно:
д = | Акₒ + Биₒ + Цзₒ | / √ (А² + Б² + Ц²).
Ако је дата тачка К0 је на другој страни равни П, попут исходишта, затим између вектора ρ-ρ0 и в је туп угао, дакле:
д = - (ρ -ρ0, в) = (ρ0, в) -п> 0.
У случају када је тачка К0 заједно са исходиштем координата налази се на истој страни П, тада је створени угао оштар, то јест:
д = (ρ-ρ0, в) = р - (ρ0, в)> 0.
Као резултат тога, испоставља се да је у првом случају (ρ0, в)> р, у другом (ρ0, в) <п.
Тангентна равнина на површину у тачки тангенте Мº је равнина која садржи све могуће тангенте на кривине повучене кроз ову тачку на површини.
Са овим обликом једначине површине Ф (к, и, з) = 0, једначина тангентне равни у додирној тачки Мº (кº, иº, зº) ће изгледати овако:
Фк(кº, иº, зº) (к-кº) + Ф.к(кº, иº, зº) (и-иº) + Фк(кº, иº, зº) (з-зº) = 0.
Ако поставимо површину у експлицитан облик з = ф (к, и), тада ће тангентна раван бити описана једначином:
з-зº = ф (кº, иº) (к- кº) + ф (кº, иº) (и-иº).
Систем се налази у тродимензионалном просторукоординате (правоугаоне) Окиз, дате су две равни П ′ и П ″, које се секу и не подударају. Пошто је било која раван у правоугаоном координатном систему одређена општом једначином, претпоставићемо да су П ′ и П ″ дате једначинама Ак + Б′и + Ц′з + Д ′ = 0 и А ″ к + Б ″ и + Ц ″ з + Д ″ = 0. У овом случају имамо нормалну н ′ (А ′, Б ′, Ц ′) равни П ′ и нормалну н ″ (А ″, Б ″, Ц ″) равни П ″. Пошто наше равни нису паралелне и не подударају се, ови вектори нису колинеарни. Користећи језик математике, овај услов можемо записати на следећи начин: н ′ = н ″ ↔ (А ′, Б ′, Ц ′) = (λ * А ″, λ * Б ″, λ * Ц ″), λϵР. Нека је права линија која лежи на пресеку П ′ и П ″ означена словом а, у овом случају а = П ′ ∩ П ″.
а је права линија која се састоји од скупа свих тачака(заједничке) равни П ′ и П ″. То значи да координате било које тачке која припада правој а мора истовремено задовољити једначине А'к + Б'и + Ц'з + Д '= 0 и А ″ к + Б ″ и + Ц ″ з + Д ″ = 0. То значи да ће координате тачке бити посебно решење следећег система једначина:

Као резултат тога, испоставља се да је решење (опште) овогасистем једначина ће одредити координате сваке од тачака праве линије, које ће деловати као пресечна тачка П ′ и П ″, и одредити праву линију а у Окиз координатном систему (правоугаоног) у простору.


























