
Геометрија је егзактна и сложена наука,која је уз све ово једна врста уметности. Линије, авиони, пропорције - све ово помаже у стварању много заиста лепих ствари. И што је чудно, ово се заснива на геометрији у различитим облицима. У овом чланку ћемо погледати једну врло необичну ствар која је директно повезана са овим. Златни пресек је управо геометријски приступ о коме ће бити речи.
Људи се најчешће воде обликом предмета.како би га препознали међу милионима других. По облику одређујемо какве ствари стоје испред нас или стоје у даљини. Људе првенствено препознајемо по облику тела и лица. Стога можемо поуздано тврдити да су сам облик, његова величина и изглед једна од најважнијих ствари у људској перцепцији.
За људе облик представља било штаинтересовање из два главна разлога: или је диктирано виталном нужношћу, или је узроковано естетским задовољством лепоте. Најбоља визуелна перцепција и осећај склада и лепоте најчешће долази када особа посматра облик у чијој је конструкцији коришћена симетрија и посебан однос, који се назива златни пресек.
Дакле, златни пресек је златни пресек,што је такође хармоничка подела. Да бисмо ово јасније објаснили, размотримо неке од карактеристика форме. Наиме: форма је нешто целина, али целина се пак увек састоји од неких делова. Ови делови ће вероватно имати различите карактеристике, барем различите величине. Па такве димензије су увек у одређеном односу, како међу собом, тако и у односу на целину.

Дакле, другим речима, то можемо тврдитизлатни пресек је однос две величине, који има своју формулу. Коришћење овог односа при креирању облика помаже да се учини што лепшим и хармоничнијим за људско око.
Златни пресек се често користи утренутно веома различите сфере живота. Али историја овог концепта сеже у давна времена, када су се науке попут математике и филозофије тек појавиле. Као научни концепт, златни пресек је ушао у употребу за време Питагоре, наиме у 6. веку пре нове ере. Али чак и пре тога, знање о таквом односу коришћено је у пракси у старом Египту и Вавилону. Живописан доказ за то су пирамиде, за чију су изградњу кориштене управо такве златне пропорције.
Ренесанса је постала нови дах захармонијску поделу, посебно захваљујући Леонарду да Винчију. Овај однос се почео све више користити и у егзактним наукама, попут геометрије, и у уметности. Научници и уметници почели су дубље да проучавају златни пресек и стварају књиге које се баве овим питањем.
Једно од најважнијих историјских дела,повезана са златним пресеком је књига Луце Панцхолија под насловом „Божански удео“. Историчари сумњају да је илустрације у овој књизи урадио сам Леонардо пре Винција.
Математика даје врло јасну дефиницијупропорција, што указује да је то једнакост два односа. Математички, ово се може изразити следећом једнакошћу: а: б = ц: д, где су а, б, ц, д неке одређене вредности.

Ако узмемо у обзир удео сегмента подељен на два дела, можемо се срести у само неколико ситуација:
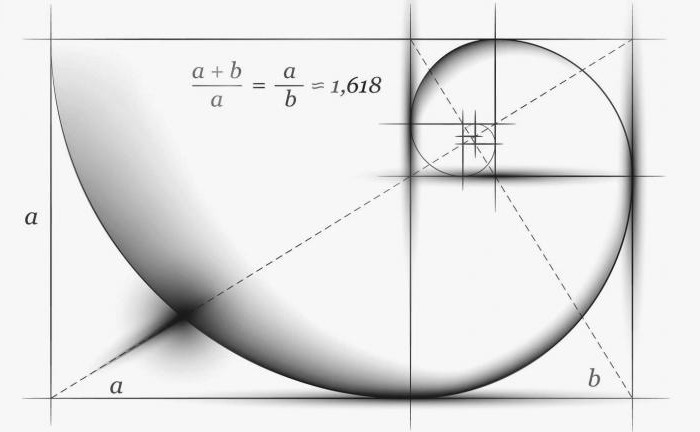
Што се тиче златног пресека, ово јепропорционална подела сегмента на неједнаке делове, када цео сегмент припада већем делу, као и сам већи део припада мањем. Постоји још једна формула: мањи сегмент се односи на већи, а већи на цео сегмент. У математичком смислу то изгледа овако: а: б = б: ц или ц: б = б: а. Ово је облик формуле златног пресека.
Златни пресек, примери којих смо садасматра, односи се на невероватне појаве у природи. Ово су веома лепи примери чињенице да математика нису само бројеви и формуле, већ наука, која има више од стварног одраза у природи и нашем животу уопште.

За живе организме, један од главних животазадаци је раст. Таква жеља да заузме своје место у свемиру, у ствари, спроводи се у неколико облика - раст према горе, скоро хоризонтално ширење по тлу, или увијање у спиралу на некој врсти ослонца. И колико год да је невероватно, многе биљке расту у складу са златним пресеком.
Још једна готово невероватна чињеница су односиу телу гуштера. Њихово тело изгледа довољно пријатно за људско око, а то је могуће захваљујући истом златном пресеку. Да будемо прецизнији, дужина њиховог репа односи се на дужину целог тела као 62: 38.
Златни пресек је заиста невероватан концепт, што значи да кроз историју можемо пронаћи многе заиста занимљиве чињенице о таквој пропорцији. Овде су неки од њих:

Овај одељак треба поменути веома значајанлице, и то - С. Зеисинг. Ово је немачки истраживач који је учинио огроман посао на пољу проучавања златног пресека. Објавио је рад под називом Естетско истраживање. У свом делу је златни пресек представио као апсолутни појам који је универзалан за све појаве, како у природи тако и у уметности. Овде се можете сетити златног пресека пирамиде заједно са складном пропорцијом људског тела и тако даље.
Зеисинг је био тај који је успео да докаже то златопресек је, у ствари, просечан статистички закон за људско тело. То се показало у пракси, јер је током свог рада морао да мери много људских тела. Историчари верују да је више од две хиљаде људи учествовало у овом искуству. Према Зеисинговом истраживању, главни показатељ златног пресека је подела тела по тачки пупка. Дакле, мушко тело са просечним односом 13: 8 је нешто ближе златном пресеку него женско тело, где је златни пресек 8: 5. Такође, златни пресек се може посматрати и у другим деловима тела, као што је, на пример, шака.
У ствари, изградња златног пресека је стварједноставно. Као што видимо, чак су се и стари људи са тим носили прилично лако. Шта можемо рећи о савременим знањима и технологијама човечанства. У овом чланку нећемо показати како се то може учинити једноставно на комаду папира и са оловком у руци, али са поуздањем кажемо да је то заиста могуће. Штавише, то се може учинити на више начина.
Пошто је ово прилично једноставна геометрија,златни пресек је прилично једноставан за изградњу чак и у школи. Стога се информације о овоме могу лако пронаћи у специјализованим књигама. Проучавајући златни пресек, 6. разред је у потпуности способан да разуме принципе његове конструкције, што значи да су чак и деца довољно паметна да савладају такав задатак.
Прво упознавање златног пресека у пракси почиње једноставном поделом праволинијског сегмента, све у истим пропорцијама. Најчешће се то ради помоћу равнала, шестара и, наравно, оловке.
Сегменти златног пресека изражени су каобесконачни ирационални разломак АЕ = 0,618 ..., ако се АБ узме као јединица, БЕ = 0,382 ... Да би се ови прорачуни учинили практичнијим, често се користе не тачне, већ приближне вредности, наиме - 0,62 и 0 , 38. Ако се сегмент АБ узме као 100 делова, онда ће већина бити једнака 62, али ће мањи бити 38 делова.

Главно својство златног пресека може се изразити једначином: к2-к-1 = 0. Приликом решавања добијамо следеће корене: к1,2=. Иако је математика егзактна и ригорозна наука, попут њеног одељка - геометрије, али управо та својства као што су закони златног пресека уносе мистерију у ову тему.
Да резимирамо, размотримо укратко оно што је већ речено.
Углавном под владавином златног пресекапостоји много примера уметности, где је однос близу 3/8 и 5/8. Ово је груба формула за златни рез. У чланку је већ било доста речи о примерима коришћења одељка, али ћемо га поново погледати кроз призму античке и модерне уметности. Дакле, најупечатљивији примери из давних времена:

Што се тиче већ вероватно свесногупотреба пропорције, дакле, почевши од времена Леонарда да Винчија, ушла је у употребу у готово свим гранама живота - од науке до уметности. Чак су и биологија и медицина доказале да златни пресек делује чак и у живим системима и организмима.


























