
En trapezoid är ett speciellt fall av en fyrkant,vilket ett par sidor är parallellt. Termen "trapezoid" härrör från det grekiska ordet τράπεζα, som betyder "tabell", "tabell". I den här artikeln kommer vi att ta hänsyn till typen av trapezoid och dess egenskaper. Dessutom kommer vi att räkna ut hur man beräknar de enskilda elementen i denna geometriska figur. Till exempel diagonalen i en likgiltig trapezoid, mellanlinjen, området etc. Materialet presenteras i stil med elementär populär geometri, det vill säga i en lättillgänglig form.
Låt oss först ta reda på vad som ärfyrhörning. Denna siffra är ett speciellt fall av en polygon som innehåller fyra sidor och fyra vertikaler. Två hörn i en fyrkant som inte ligger intill kallas motsatta. Detsamma kan sägas om två sidor som inte är angränsande. Huvudtyperna av fyrkantar är ett parallellogram, en rektangel, en romb, en fyrkant, en trapezoid och en deltoid.

Så tillbaka till trapezoid.Som vi redan sagt, i denna siffra är de två sidorna parallella. De kallas baser. De andra två (icke-parallella) är sidorna. I examina och olika provmaterial är det ofta möjligt att möta problem förknippade med trapes, varvid lösningen ofta kräver att studenten har kunskap som inte tillhandahålls i programmet. Skolgeometri-kursen introducerar eleverna egenskaper hos vinklar och diagonaler, liksom mittlinjen för en isosceles trapezoid. Men utöver detta har den nämnda geometriska figuren andra funktioner. Men om dem lite senare ...
Det finns många typer av denna siffra. Men vanligtvis är det vanligt att ta hänsyn till två av dem - likben och rektangulära.
1. En rektangulär trapezoid är en figur där en av sidorna är vinkelrätt mot baserna. Hon har två vinklar alltid lika med nittio grader.
2. En likgiltig trapezoid är en geometrisk figur där sidorna är lika. Detta innebär att vinklarna vid baserna också är parvis lika.

Huvudprincipen är användningen avden så kallade uppdragsmetoden. I själva verket finns det inget behov av att införa nya egenskaper hos denna figur i kursen i teoretisk geometri. De kan upptäckas och formuleras i processen för att lösa olika problem (bättre än systemproblem). Samtidigt är det mycket viktigt att läraren vet vilka uppgifter som måste ställas in för eleverna vid en eller annan tid i inlärningsprocessen. Dessutom kan varje trapezoidegenskap representeras som en nyckeluppgift i uppgiftssystemet.
Den andra principen är den så kalladespiralorganisering av studien av trapesens "anmärkningsvärda" egenskaper. Detta innebär en återgång i inlärningsprocessen till enskilda egenskaper hos en given geometrisk figur. Detta gör det lättare för eleverna att memorera dem. Till exempel egenskapen på fyra punkter. Det kan bevisas både genom att studera likheten och därefter använda vektorer. Och lika storleken på trianglarna intill figurens laterala sidor kan bevisas genom att man inte bara tillämpar egenskaperna hos trianglar med lika höjder som dragits till sidorna som ligger på en rak linje utan också med formeln S = 1/2 (ab * sinα). Dessutom kan du räkna ut sines på en inskriven trapez eller en rätvinklig triangel på en beskriven trapez, etc.
Tillämpning av "off-program" -funktionerden geometriska figuren i innehållet i skolkursen är uppgiftsteknologin för deras undervisning. Ständig överklagande av de studerade egenskaperna medan de fyller i andra ämnen gör det möjligt för eleverna att få en djupare förståelse för trapezoid och säkerställer framgången med att lösa de tilldelade uppgifterna. Så, låt oss gå ner för att studera denna underbara figur.

Som vi redan har noterat är denna geometriskasiffrorna på sidorna är lika. Det är också känt som en vanlig trapes. Och varför är det så anmärkningsvärt och varför fick det ett sådant namn? Särdragen i denna figur inkluderar det faktum att den inte bara har samma sidor och vinklar vid baserna utan också diagonalerna. Dessutom är summan av vinklarna för en likbent trapezoid 360 grader. Men det är inte allt! Av alla kända trapezoider är det bara runt en likbenad man som kan beskriva en cirkel. Detta beror på det faktum att summan av motsatta vinklar i denna figur är 180 grader, och endast under detta tillstånd kan en cirkel beskrivas runt en fyrkant. Nästa egenskap hos den betraktade geometriska figuren är att avståndet från basens topp till projektionen av det motsatta toppunktet till den raka linjen som innehåller denna bas är lika med mittlinjen.
Låt oss nu ta reda på hur man hittar vinklarna på en likbent trapez. Tänk på en lösning på detta problem, förutsatt att dimensionerna på figurens sidor är kända.
Vanligtvis betecknas fyrsidan vanligtvisbokstäverna A, B, C, D, där BS och HELL är grunden. I ett likartat trapez är sidorna lika. Vi antar att deras storlek är lika med X och att basernas storlek är lika med Y och Z (mindre respektive större). För att utföra beräkningen är det nödvändigt att rita höjden H från vinkel B. Resultatet är en rätvinklig triangel ABN, där AB är hypotenusen, och BN och AN är benen. Vi beräknar storleken på benet AH: subtraherar det mindre från den större basen och delar resultatet med 2. Vi skriver det i form av formeln: (Z-Y) / 2 = F. För att beräkna den spetsiga vinkeln för triangeln använder vi cos-funktionen. Vi får följande post: cos (β) = X / F. Nu beräknar vi vinkeln: β = arcos (X / F). Vidare, med kännedom om en vinkel, kan vi bestämma den andra, för detta utför vi en elementär aritmetisk operation: 180 - β. Alla vinklar är definierade.
Det finns också en andra lösning på detta problem. I början sänker vi höjden N. från hörnet. Beräkna värdet på benet BN. Vi vet att kvadraten av hypotenusen i en rätvinklig triangel är lika med summan av benens kvadrater. Vi får: BN = √ (X2-F2). Därefter använder vi den trigonometriska funktionen tg. Som ett resultat har vi: β = arctan (BN / F). Ett skarpt hörn hittades. Därefter definierar vi en tråkig vinkel på samma sätt som i den första metoden.
Låt oss först skriva ner fyra regler. Om diagonalerna i en likbent trapes är vinkelräta, då:
- figurens höjd kommer att vara lika med summan av baserna, dividerat med två;
- dess höjd och mittlinje är lika;
- trapezoidens yta kommer att vara lika med höjningens kvadrat (mittlinjen, halva summan av baserna);
- diagonalens kvadrat är lika med hälften av kvadraten av summan av baserna eller två gånger kvadraten för mittlinjen (höjd).
Tänk nu på formlerna som definierar diagonalen för en likbent trapez. Detta informationsblock kan grovt delas in i fyra delar:
1. Formel för längden på en diagonal genom dess sidor.
Vi antar att A är bottenbotten, B är toppen, C är lika sidor, D är diagonalen. I detta fall kan längden bestämmas enligt följande:
D = √ (C2 + A * B).
2. Formler för diagonalens längd av kosinosatsningen.
Vi accepterar att A är den nedre basen, B är den övre,C - lika sidor, D - diagonal, α (vid den nedre basen) och β (vid den övre basen) - trapetsvinklar. Vi får följande formler som du kan beräkna diagonalens längd:
- D = √ (A2 + C2-2A * C * cosa);
- D = √ (A2 + C2-2A * C * cosp);
- D = √ (B2 + C2-2B * C * cosp);
- D = √ (B2 + C2-2B * C * cosα).
3. Formler för längden på diagonalerna för en likbent trapez.
Vi antar att A är bottenbotten, B är toppen, D är diagonalen, M är mittlinjen, H är höjden, P är området för trapezoid, α och β är vinklarna mellan diagonalerna. Vi bestämmer längden med följande formler:
- D = √ (M2 + H2);
- D = √ (H2 + (A + B) 2/4);
- D = √ (H (A + B) / sinα) = √ (2P / sinα) = √ (2M * H / sinα).
I det här fallet är likheten sann: sinα = sinβ.
4. Formler för längden på diagonalen i termer av sidor och höjd.
Vi antar att A är bottenbotten, B är toppen, C är sidorna, D är diagonalen, H är höjden, α är vinkeln vid bottenbotten.
Vi bestämmer längden med följande formler:
- D = √ (H2 + (A-P * ctgα) 2);
- D = √ (H2 + (B + P * ctgα) 2);
- D = √ (A2 + C2-2A * √ (C2-H2)).

Låt oss titta på vad som är intressant med denna geometriska figur. Som vi sa har en rektangulär trapets två rätt vinklar.
Förutom den klassiska definitionen finns det ocksåandra. Till exempel är en rektangulär trapezoid en trapezoid med en sida vinkelrät mot dess baser. Eller en figur med rät vinkel på sidosidan. För denna typ av trapets är höjden lika med sidosidan, som är vinkelrät mot baserna. Mittlinjen är linjesegmentet som förbinder de två sidornas mittpunkter. Egenskapen hos det nämnda elementet är att det är parallellt med baserna och är lika med hälften av deras summa.
Låt oss nu titta på de grundläggande formlerna,definierar denna geometriska figur. För detta antar vi att A och B är fundament; C (vinkelrätt mot baserna) och D - sidor av en rektangulär trapez, M - mittlinje, α - spetsig vinkel, P - område.
ett.Den laterala sidan, vinkelrät mot baserna, är lika med figurens höjd (C = H) och är lika med produkten av längden på den andra laterala sidan D och sinusen för vinkeln a med en större bas ( C = D * sina). Dessutom är det lika med produkten av tangenten för den spetsiga vinkeln a och skillnaden mellan baserna: C = (A-B) * tgα.
2. Sidosidan D (inte vinkelrät mot baserna) är lika med kvoten för skillnaden mellan A och B och cosinus (α) för den spetsiga vinkeln eller kvoten för höjden på figuren H och sinus på spetsig vinkel: D = (AB) / cos α = C / sinα.
3. Sidosidan, som är vinkelrät mot baserna, är lika med kvadratroten av skillnaden mellan kvadraten D - den andra sidan - och kvadraten för skillnaden mellan baserna:
C = √ (D2- (A-B) 2).
4. Sidan D på en rektangulär trapets är lika med kvadratroten av summan av kvadraten på sidan C och kvadraten på skillnaden mellan baserna för den geometriska figuren: D = √ (C2 + (A-B) 2).
5. Sidan av C är lika med kvoten för att dela dubbelarean med summan av dess baser: C = P / M = 2P / (A + B).
6. Arean bestäms av produkten M (mittlinjen för en rektangulär trapets) av höjden eller sidan vinkelrätt mot baserna: P = M * H = M * C.
7. Sidan C är lika med kvoten för att dividera figurens dubbla område med produkten av sinus med en spetsig vinkel och summan av dess baser: C = P / M * sinα = 2P / ((A + B) * sinα).
8. Formler för den laterala sidan av en rektangulär trapetsform genom dess diagonaler och vinkeln mellan dem:
- sina = sinp;
- C = (D1 * D2 / (A + B)) * sinα = (D1 * D2 / (A + B)) * sinp,
där D1 och D2 är trapezoidens diagonaler; α och β är vinklarna mellan dem.
9. Formler för lateralsidan genom vinkeln vid den nedre basen och andra sidor: D = (A-B) / cosα = C / sinα = H / sinα.
Eftersom en trapezoid med rät vinkel är ett speciellt fall av en trapezoid kommer resten av formlerna som definierar dessa figurer att motsvara en rektangulär.

Om villkoret säger att en cirkel är inskriven i en rektangulär trapets, kan följande egenskaper användas:
- summan av baserna är lika med summan av sidorna;
- avstånden från toppen av den rektangulära formen till tangentpunkterna för den inskrivna cirkeln är alltid lika;
- trapesens höjd är lika med sidosidan, vinkelrät mot baserna och lika med cirkelns diameter;
- cirkelns centrum är den punkt vid vilken halvorna i hörnen skär varandra;
- om den laterala sidan delas med tangenspunkten i segmenten H och M, är cirkelns radie lika med kvadratroten av produkten av dessa segment;
- en fyrkant bildad av kontaktpunkterna, trapezens topp och centrum av den inskrivna cirkeln - detta är en fyrkant vars sida är lika med radien;
- figurens yta är lika med basens produkt och produkten av basens halvsumma med sin höjd.
Detta ämne är mycket praktiskt för att studera fastigheter.denna geometriska form. Till exempel delar diagonaler trapezoid i fyra trianglar, och de som ligger intill baserna är lika och sidorna är lika. Detta uttalande kan kallas en egenskap av trianglar i vilka en trapetsform delas med sina diagonaler. Den första delen av detta uttalande bevisas genom likhetstecknet i två vinklar. För att bevisa den andra delen är det bättre att använda metoden nedan.
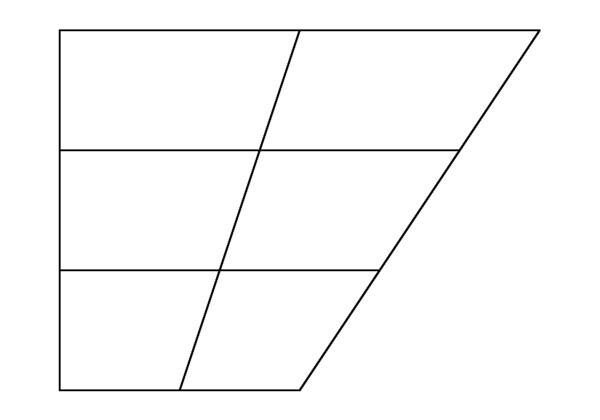
Vi accepterar att siffran för ABSD (BP och BS är grundernatrapezium) divideras med VD- och AC-diagonalerna. Korsningen är O. Vi får fyra trianglar: AOS - vid den nedre basen, BOS - vid den övre basen, ABO och SOD vid sidosidorna. Trianglar SOD och BFB har en gemensam höjd om segmenten BO och OD är deras baser. Vi får att skillnaden mellan deras områden (P) är lika med skillnaden mellan dessa segment: PBOS / PSOD = BO / OD = K. Därför är PSOD = PBOS / K. Likaså har trianglarna BFB och AOB en gemensam höjd. Vi tar segmenten SB och OA för deras baser. Vi får PBOS / PAOB = SO / OA = K och PAOB = PBOS / K. Det följer av detta att PSOD = PAOB.
För att konsolidera materialet rekommenderas studenterhitta kopplingen mellan områdena för de erhållna trianglarna, i vilka trapesformen delas med sina diagonaler, och lösa följande problem. Det är känt att områdena för biofeedback och AOD-trianglar är lika; det är nödvändigt att hitta området för trapezoid. Eftersom PSOD = PAOB betyder det att PABSD = PBOS + PAOD + 2 * PSOD. Av likheten mellan trianglarna BFB och AOD följer att BO / OD = √ (PBOS / PAOD). Därför PBOS / PSOD = BO / OD = √ (PBOS / PAOD). Vi får PSOD = √ (PBOS * PAOD). Därefter PABSD = PBOS + PAOD + 2 * √ (PBOS * PAOD) = (√ PSOS + √ PAOD) 2.
Fortsätter att utveckla detta ämne kan man bevisa ochandra intressanta egenskaper hos trapezider. Så med hjälp av likhet kan man bevisa egenskapen hos ett segment som passerar genom en punkt bildad genom skärningspunkten mellan diagonalerna i denna geometriska figur, parallellt med baserna. För att göra detta löser vi följande problem: det är nödvändigt att hitta längden på det segment RK som passerar genom punkten O. Från likheten mellan trianglarna AOD och BFB följer att AO / OS = AD / BS. Av likheten mellan trianglarna AOR och ASB följer att AO / AC = RO / BS = HELL / (BS + HELL). Härifrån får vi det RO = BS * HELL / (BS + HELL). På samma sätt följer det av likheten mellan trianglarna DOK och DBS att OK = BS * HELL / (BS + HELL). Härifrån får vi det RO = OK och RK = 2 * BS * HELL / (BS + HELL). Segmentet som passerar genom skärningspunkten mellan diagonalerna, parallellt med baserna och förbinder de två sidorna, halveras av skärningspunkten. Dess längd är det harmoniska medelvärdet av figurens bas.
Tänk på följande trapezkvalitet, vilkenkallas fyrpunktsegenskapen. Korsningspunkterna för diagonalerna (O), skärningspunkten för förlängningen av sidosidorna (E), liksom mittpunkterna för baserna (T och G) ligger alltid på samma linje. Detta bevisas lätt med likhetsmetoden. De resulterande trianglarna BES och AED är lika, och i var och en av dem delar medianerna ET och EZ vinkeln vid toppunkten E i lika delar. Följaktligen ligger punkterna E, T och on på en rak linje. På samma sätt ligger punkterna T, O och Zh på en rak linje, allt detta följer av likheten mellan trianglarna BFB och AOD. Av detta drar vi slutsatsen att alla fyra punkterna - E, T, O och F - kommer att ligga på en rak linje.
Med hjälp av sådana trapetser kan vi erbjudaeleverna hittar längden på segmentet (LF), som delar upp figuren i två liknande. Detta segment måste vara parallellt med baserna. Eftersom de erhållna trapezierna ALPD och LBSF är lika är BS / LF = LF / BP. Det följer att LF = √ (BS * HELL). Vi får att segmentet som delar trapesformen i två liknande har en längd som är lika med det geometriska medelvärdet av längderna på figurens baser.
Tänk på följande likhetsegenskap.Den är baserad på ett segment som delar trapesformen i två lika stora figurer. Vi antar att ABSD-trapetsen är uppdelad av segmentet ЕН i två liknande. Från toppen av B tappas höjden, vilken delas av segmentet EH i två delar - B1 och B2. Vi får: PABSD / 2 = (BS + EH) * B1 / 2 = (HELL + EH) * B2 / 2 och PABSD = (BS + HELL) * (B1 + B2) / 2. Därefter komponerar vi ett system, vars första ekvation är (BS + EH) * B1 = (AD + EH) * B2 och den andra (BS + EH) * B1 = (BS + HELL) * (B1 + B2) / 2. Av detta följer att B2 / B1 = (BS + EH) / (AD + EH) och BS + EH = ((BS + HELL) / 2) * (1 + B2 / B1). Vi får att längden på segmentet som delar trapezoid i två lika stora är lika med rotens medelkvadrat för basernas längder: √ ((BS2 + AD2) / 2).
Således har vi bevisat att:
1. Segmentet som förbinder mittpunkterna på sidosidorna vid trapezoid är parallellt med BP och BS och är lika med det aritmetiska medelvärdet för BS och BP (längden på trapezens bas).
2. Linjen som passerar genom punkten O i skärningspunkten mellan diagonalerna parallellt med HELL och BS kommer att vara lika med det harmoniska medelvärdet av antalet HELL och BS (2 * BS * HELL / (BS + HELL)).
3. Segmentet som delar trapesformen i liknande har längden på det geometriska medelvärdet av baserna för BS och BP.
4. Elementet som delar upp figuren i två lika stora storlekar har längden på det genomsnittliga kvadratantalet BP och BS.
Att konsolidera materialet och förstå sambandet mellande studerade segmenten måste studenten bygga dem för en specifik trapets. Han kan enkelt visa mittlinjen och segmentet som passerar genom punkten O - skärningspunkten mellan figurens diagonaler - parallellt med baserna. Men var kommer den tredje och fjärde att vara? Detta svar kommer att leda studenten att upptäcka det önskade förhållandet mellan medelvärden.
Tänk på följande egenskaper i denna figur.Vi antar att segmentet MH är parallellt med baserna och delar diagonalerna i hälften. Korsningspunkterna kommer att kallas Ш och Ш. Detta segment kommer att vara lika med halvskillnaden mellan baserna. Låt oss titta närmare på detta. MSh - mittlinjen i ABS-triangeln, den är lika med BS / 2. MCh är mittlinjen i ABD-triangeln, den är lika med BP / 2. Då får vi att SHSH = MSH-MSH, därför SHSH = HELL / 2-BS / 2 = (HELL + VS) / 2.
Låt oss se hur det bestämsdetta element för den angivna geometriska formen. För att göra detta är det nödvändigt att förlänga baserna i motsatta riktningar. Vad betyder det? Det är nödvändigt att lägga till den nedre till den övre basen - till vardera sidan, till exempel till höger. Och förläng den nedre längden på den övre till vänster. Därefter kopplar vi dem med en diagonal. Skärningspunkten för detta segment med figurens mittlinje är trapesens tyngdpunkt.
Låt oss lista funktionerna i sådana former:
1. En trapes kan skrivas in i en cirkel endast om den är likbenig.
2. En trapes kan beskrivas runt en cirkel, förutsatt att summan av längderna på deras baser är lika med summan av längden på sidosidorna.
Inskrivna cirkelkonsekvenser:
1. Höjden på den beskrivna trapezoid är alltid lika med två radier.
2. Den beskrivna trapesens laterala sida observeras från cirkelns centrum i rät vinkel.
Den första följan är uppenbar och för bevisetdet andra krävs att man fastställer att SOD-vinkeln är rätt, vilket faktiskt inte heller kommer att vara svårt. Men kunskap om den här egenskapen gör att du kan använda en rätvinklig triangel när du löser problem.
Låt oss nu konkretisera dessa konsekvenser fören likbent trapez som är inskriven i en cirkel. Vi får att höjden är det geometriska medelvärdet av figurens bas: H = 2R = √ (BS * HELL). Medan man tränar i den grundläggande tekniken för att lösa problem för trapezoider (principen att hålla två höjder), måste studenten lösa följande uppgift. Vi antar att BT är höjden på den likbeniga figuren i ABSD. Det är nödvändigt att hitta segmenten AT och TD. Med hjälp av formeln som beskrivs ovan blir det inte svårt att göra detta.
Låt oss nu ta reda på hur man bestämmer radiencirkel med hjälp av området för den avgränsade trapetsen. Vi sänker höjden från toppen B till basen av blodtrycket. Eftersom cirkeln är inskriven i trapezoid, då BS + HELL = 2AB eller AB = (BS + HELL) / 2. Från triangeln ABN hittar vi sinα = BN / AB = 2 * BN / (BS + HELL). PABSD = (BS + HELL) * BN / 2, BN = 2R. Vi får PABSD = (BS + HELL) * R, det följer att R = PABSD / (BS + HELL).
.

Nu är det dags att gå vidare till det sista elementet i denna geometriska form. Låt oss ta reda på vad mitten av trapezoid (M) är:
1. Genom baserna: M = (A + B) / 2.
2. Genom höjd, bas och hörn:
• M = A-H * (ctga + ctgp) / 2;
• M = B + H * (ctga + ctgp) / 2.
3. Genom höjden, diagonalerna och vinkeln mellan dem. Till exempel är D1 och D2 diagonalerna för en trapets; α, β - vinklar mellan dem:
M = D1 * D2 * sina / 2H = D1 * D2 * sinp / 2H.
4. Genom området och höjden: M = P / N.


























