
В пространстве плоскость можно задавать разными начини (една точка и вектор, две точки и вектор, три точки и т.н.). Имайки предвид това, уравнението на равнината може да има различни форми. Също така, при определени условия, равнините могат да бъдат успоредни, перпендикулярни, пресичащи се и т.н. Ще поговорим за това в тази статия. Ще научим как да направим общо уравнение на равнината и не само.
Да предположим, че има интервал R3която има правоъгълна координатна система XYZ. Определяме вектор α, който ще се освободи от началната точка O. През края на вектора α изчертаваме равнина, която е перпендикулярна на него.
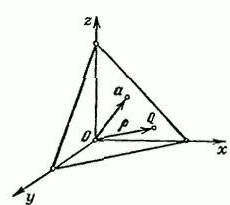
Обозначаваме в произволна точка Q = (x, y, z). Векторът на радиуса на точката Q се записва с буквата p. В този случай дължината на вектора α е равна на p = IαI и Ʋ = (cosα, cosβ, cosγ).
Това е единичен вектор, който сочи къмстрана, както и вектор α. α, β и γ са ъглите, които се образуват между вектора Ʋ и положителните посоки на космическите оси x, y, z, съответно. Проекцията на всяка точка QϵП върху вектора Ʋ е постоянна стойност, която е равна на p: (p, Ʋ) = p (p≥0).
Горното уравнение има смисъл, когато p = 0.Единственото нещо е, че в този случай равнината P ще се пресича с точката O (α = 0), която е началото, а единичният вектор Ʋ, излъчен от точката O, ще бъде перпендикулярен на P, независимо от посоката му, което означава, че векторът Ʋ се определя с точен към знака. Предишното уравнение е уравнението на нашата равнина P, изразено във векторна форма. Но по координати, външният му вид ще бъде такъв:

P тук е по-голямо или равно на 0. Намерихме уравнението на равнината в пространството в нормална форма.
Ако умножим уравнението в координати по всяко число, което не е нула, получаваме уравнение, което е еквивалентно на даденото, което определя една и съща равнина. Ще изглежда така:

Тук A, B, C са числа, които едновременно са ненулеви. Това уравнение се нарича общо уравнение на равнината.
Общото уравнение може да се променя при наличие на допълнителни условия. Нека разгледаме някои от тях.
Да предположим, че коефициентът A е 0. Това означава, че тази равнина е успоредна на дадената ос Ox. В този случай формата на уравнението ще се промени: Vu + Cz + D = 0.
По същия начин формата на уравнението ще се промени при следните условия:
В случая, когато числата A, B, C, D са различни от нула, формата на уравнение (0) може да бъде следната:
x / a + y / b + z / c = 1,
в която a = -D / A, b = -D / B, c = -D / C.
В резултат на това получаваме уравнението на равнината в сегменти. Трябва да се отбележи, че тази равнина ще пресича оста Ox в точка с координати (a, 0,0), Oy - (0, b, 0) и Oz - (0,0, c).

Като се вземе предвид уравнението x / a + y / b + z / c = 1, е лесно визуално да се представи местоположението на равнината спрямо дадена координатна система.
Нормалният вектор n към равнината P има координати, които са коефициентите на общото уравнение на тази равнина, тоест n (A, B, C).

За да се определят координатите на нормалното n, достатъчно е да се знае общото уравнение на дадената равнина.
Когато използвате уравнение в редови сегменти, коитоима формата x / a + y / b + z / c = 1, тъй като когато използвате общото уравнение, можете да запишете координатите на всеки нормален вектор на дадена равнина: (1 / a + 1 / b + 1 / c).
Заслужава да се отбележи, че нормалният вектор помагарешават различни проблеми. Най-често срещаните проблеми включват проблема за доказване на перпендикулярността или успоредността на равнините, проблемът с намирането на ъглите между равнините или ъглите между равнините и линиите.
Ненулев вектор n, перпендикулярен на дадена равнина, се нарича нормален (нормален) за дадена равнина.
Да предположим, че в координатно пространство (правоъгълна координатна система) Oxyz са дадени:

Необходимо е да се състави уравнение за равнина, която ще премине през точката Mₒ, перпендикулярна на нормалното n.
В пространството избираме произволна точка иобозначаваме го с M (xy, z). Нека радиусният вектор на всяка точка M (x, y, z) е r = x * i + y * j + z * k, а радиусният вектор на точката Mₒ (xₒ, yₒ, zₒ) - rₒ = xₒ * i + yₒ * j + zₒ * k. Точката М ще принадлежи на дадената равнина, ако векторът МₒМ е перпендикулярен на вектора n. Нека напишем условието на ортогоналност, използвайки точков продукт:
[МₒМ, n] = 0.
Тъй като МₒМ = r - rₒ, векторното уравнение на равнината ще изглежда така:
[r - rₒ, n] = 0.
Това уравнение може да има друга форма. За това се използват свойствата на точков продукт, а лявата част на уравнението се трансформира. [r - rₒ, n] = [r, n] - [rₒ, n]. Ако [rₒ, n] се обозначава като c, тогава получаваме следното уравнение: [r, n] - c = 0 или [r, n] = c, което изразява постоянството на проекциите върху нормалния вектор на радиусните вектори на дадени точки, които принадлежат на равнината.
Сега можете да получите координатната форма на писане на векторното уравнение на нашата равнина [r - rₒ, n] = 0. Тъй като r - rₒ = (x - xₒ) * i + (y - yₒ) * j + (z - zₒ) * k, и n = A * i + B * j + C * k, имаме:

Оказва се, че имаме уравнение на равнина, преминаваща през точка, перпендикулярна на нормалното n:
A * (x- xₒ) + B * (y– yₒ) C * (z - zₒ) = 0.
Нека зададем две произволни точки M '(x', y ', z') и M ″ (x ″, y ″, z ″), както и вектор a (a ′, a ″, a)
Сега ще можем да съставим уравнение на дадена равнина, което ще премине през съществуващите точки M ′ и M ″, както и всяка точка M с координати (x, y, z), успоредна на даден вектор a.
Нещо повече, векторите M'M = {x-x ′; y-y ′; zz ′} и M ″ M = {x ″ -x ′; y ″ -y ′; z ″ -z ′} трябва да са копланарни с вектора a = (a ′, a ″, a), което означава, че (M′M, M ″ M, a) = 0.
И така, нашето уравнение на равнина в космоса ще изглежда така:
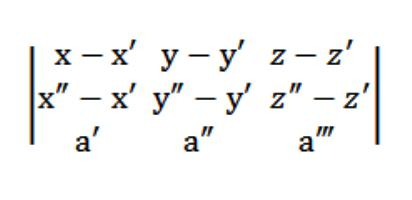
Да речем, че имаме три точки: (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴), които не принадлежат към една права линия. Необходимо е да се напише уравнението на равнината, преминаваща през дадените три точки. Теорията на геометрията твърди, че този вид равнина наистина съществува, но само тя е единствената и неподражаема. Тъй като тази равнина пресича точката (x ′, y ′, z ′), формата на нейното уравнение ще бъде следната:

Тук A, B, C са ненулеви едновременно. Също така дадената равнина пресича още две точки: (x ″, y ″, z ″) и (x ‴, y ‴, z ‴). В тази връзка трябва да бъдат изпълнени следните условия:

Сега можем да съставим хомогенна система от уравнения (линейни) с неизвестни u, v, w:

В нашия случай x, y или z е произволноточка, която отговаря на уравнение (1). Като се вземат предвид уравнението (1) и системата от уравнения (2) и (3), системата от уравнения, посочена на фигурата по-горе, се удовлетворява от вектора N (A, B, C), който е нетривиален. Ето защо детерминантата на тази система е равна на нула.
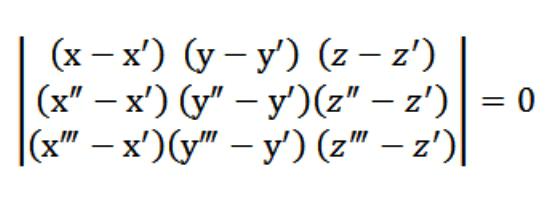
Уравнение (1), което имаме, ее уравнението на равнината. Преминава точно през 3 точки и е лесно да се провери. За да направите това, трябва да разширим нашата детерминанта чрез елементите в първия ред. От съществуващите свойства на детерминанта следва, че нашата равнина едновременно пресича три първоначално определени точки (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴). Тоест, решихме поставената пред нас задача.
Двугранният ъгъл епространствена геометрична фигура, образувана от две полуплоскости, които се излъчват от една права линия. С други думи, това е част от пространството, което е ограничено от тези полуплоскости.
Да речем, че имаме две равнини със следните уравнения:
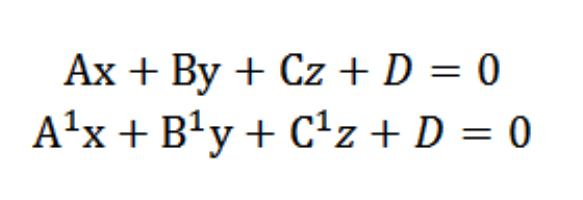
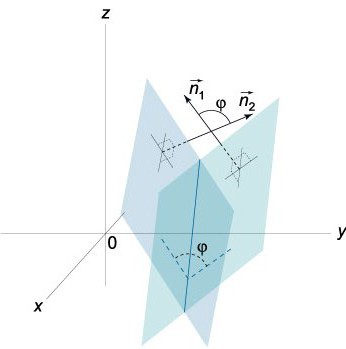
Знаем, че векторите N = (A, B, C) иN¹ = (А¹, В¹, С¹) са перпендикулярни според дадените равнини. В тази връзка ъгълът φ между векторите N и N¹ е равен на ъгъла (двугранника), който е между тези равнини. Скаларният продукт е:
NN¹ = | N || N¹ | cos φ,
именно защото
cosφ = NN¹ / | N || N¹ | = (AA¹ + BB¹ + CC¹) / ((√ (A² + B² + C²)) * (√ (A¹) ² + (B¹) ² + (C¹) ²)).
Достатъчно е да се вземе предвид, че 0≤φ≤π.
Всъщност две равнини, които се пресичат, образуват два ъгъла (двугранни): φ1 и φ2... Тяхната сума е равна на π (φ1+ φ2= π). Що се отнася до техните косинуси, техните абсолютни стойности са равни, но се различават по знаци, тоест cos φ1= -cos φ2... Ако в уравнение (0) заменим съответно A, B и C с числа -A, -B и -C, тогава полученото уравнение ще определи една и съща равнина, единственият ъгъл φ в уравнението cos φ = NN1/ | N || N1| ще бъде заменен с π-φ.
Плоскостите се наричат перпендикулярни, междукой ъгъл е 90 градуса. Използвайки описания по-горе материал, можем да намерим уравнението на равнина, перпендикулярна на друга. Да предположим, че имаме две равнини: Ax + By + Cz + D = 0 и A¹x + B¹y + C¹z + D = 0. Можем да твърдим, че те ще бъдат перпендикулярни, ако cosφ = 0. Това означава, че NN¹ = AA¹ + BB¹ + CC¹ = 0.
Паралелни са две равнини, които не съдържат общи точки.
Условието равнините да са успоредни (техните уравнениясъщото като в предишния параграф) е, че векторите N и N¹, които са перпендикулярни на тях, са колинеарни. Това означава, че са изпълнени следните условия за пропорционалност:
A / A¹ = B / B¹ = C / C¹.
Ако условията за пропорционалност са разширени - A / A¹ = B / B¹ = C / C¹ = DD¹,
това показва, че тези равнини съвпадат. Това означава, че уравненията Ax + Vy + Cz + D = 0 и A¹x + B¹y + C¹z + D¹ = 0 описват една равнина.
Да речем, че имаме равнина Р, която е даденауравнение (0). Необходимо е да се намери разстоянието до него от точката с координати (xₒ, yₒ, zₒ) = Qₒ. За да направите това, трябва да приведете уравнението на равнината P в нормална форма:
(p, v) = p (p≥0).
В този случай ρ (x, y, z) ерадиусният вектор на нашата точка Q, разположен на P, p е дължината на перпендикуляра P, който се освобождава от нулевата точка, v е единичният вектор, който се намира в посока a.

Разликата ρ-ρº на радиусния вектор на някаква точка Q = (x, y, z), принадлежаща на P, както и радиусния вектор на дадена точка Q0= (xₒ, yₒ, zₒ) е такъв вектор, абсолютната стойност на проекцията на който на v е равна на разстоянието d, което трябва да се намери от Q0= (xₒ, yₒ, zₒ) до P:
D = | (ρ-ρ0, v) |, но
(Ρ-ρ0, v) = (ρ, v) - (ρ0, v) = р– (ρ0, v).
Така се оказва
d = | (ρ0, v) -p |.
Сега видяхме да изчислим разстоянието d от Q0 към равнината П, трябва да използвате нормалната форма на уравнението на равнината, като същевременно се прехвърляте в лявата част на p и замествате (xₒ, yₒ, zₒ) в последната вместо x, y, z.
Така ще намерим абсолютната стойност на получения израз, тоест желаното d.
Използвайки езика на параметрите, получаваме очевидното:
d = | Axₒ + Byₒ + Czₒ | / √ (A² + B² + C²).
Ако дадена точка Q0 е от другата страна на равнината P, подобно на началото, след това между вектора ρ-ρ0 и v е тъп ъгъл, следователно:
d = - (ρ-ρ0, v) = (ρ0, v) -p> 0.
В случая, когато точката Q0 заедно с началото на координатите се намира от същата страна на P, тогава създаденият ъгъл е остър, т.е.
d = (ρ-ρ0, v) = p - (p0, v)> 0.
В резултат се оказва, че в първия случай (ρ0, v)> р, във втория (ρ0, v) <p.
Допирателната равнина към повърхността в точката на допир Mº е равнината, съдържаща всички възможни допирателни към кривите, начертани през тази точка на повърхността.
С тази форма на уравнението на повърхността F (x, y, z) = 0, уравнението на допирателната равнина в допирателната точка Mº (xº, yº, zº) ще изглежда така:
Fх(xº, yº, zº) (x- xº) + Fх(xº, yº, zº) (y- yº) + Fх(xº, yº, zº) (z-zº) = 0.
Ако зададем повърхността в явна форма z = f (x, y), тогава допирателната равнина ще бъде описана от уравнението:
z-zº = f (xº, yº) (x- xº) + f (xº, yº) (y-yº).
Системата се намира в триизмерно пространствокоординати (правоъгълни) Oxyz, дадени са две равнини P ′ и P ″, които се пресичат и не съвпадат. Тъй като всяка равнина в правоъгълна координатна система се определя от общото уравнение, ще приемем, че P ′ и P ″ са дадени от уравненията Ax + B′y + C′z + D ′ = 0 и A ″ x + B ″ y + C ″ z + D ″ = 0. В този случай имаме нормалната n ′ (A ′, B ′, C ′) на равнината P ′ и нормалната n ″ (A ″, B ″, C ″) на равнината P ″. Тъй като нашите равнини не са успоредни и не съвпадат, тези вектори не са колинеарни. Използвайки езика на математиката, можем да напишем това условие, както следва: n ′ ≠ n ″ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ * C ″), λϵR. Нека правата линия, която се намира в пресечната точка на P ′ и P ″, ще бъде обозначена с буквата a, в този случай a = P ′ ∩ P ″.
a е права линия, състояща се от набор от всички точки(общи) равнини P 'и P ″. Това означава, че координатите на всяка точка, принадлежаща на права линия a, трябва едновременно да удовлетворяват уравненията A'x + B'y + C'z + D '= 0 и A ″ x + B ″ y + C ″ z + D ″ = 0. Това означава, че координатите на точката ще бъдат конкретно решение на следната система от уравнения:

В резултат се оказва, че решението (общо) на товасистемата от уравнения ще определи координатите на всяка от точките на правата линия, която ще действа като пресечна точка на P ′ и P ″, и ще определи правата линия a в координатната система на Oxyz (правоъгълна) в пространството.


























