
Aprendiendo en la escuela a resolver ecuaciones en clasematemáticos, muchos estudiantes a menudo están seguros de que están perdiendo el tiempo, y sin embargo, tal habilidad es útil en la vida no solo para aquellos que deciden seguir los pasos de Descartes, Euler o Lobachevsky.
En la práctica, como la medicina o la economía,Con bastante frecuencia, hay situaciones en las que un especialista necesita saber cuándo la concentración de la sustancia activa de un medicamento en particular alcanza el nivel requerido en la sangre del paciente o si es necesario calcular el tiempo requerido para que un negocio en particular sea rentable.
Muy a menudo es una solución no linealecuaciones de varios tipos. Para hacer esto lo más rápido posible, especialmente con el uso de computadoras, permita métodos numéricos. Están bien estudiados y durante mucho tiempo se ha demostrado que son efectivos. Entre ellos está el método de la tangente de Newton, al que se dedica este artículo.

En este caso, hay una función g, que se proporciona en el intervalo (a, b) y toma ciertos valores, es decir, es posible que cada x perteneciente a (a, b) asocie un número específico g (x).
Se requiere establecer todas las raíces de la ecuación a partir del intervalo entre los puntos ayb (incluidos los extremos) para los cuales la función se pone a cero. Obviamente, estos serán los puntos de intersección de y = g (x) con OX.
En algunos casos, es más conveniente reemplazar g (x) = 0 con uno similar de la forma g1(x) = g2(x) En este caso, las raíces son las abscisas (valor x) de los puntos de intersección de los gráficos g1(x) yg2(x)
La solución de una ecuación no lineal también es importante para los problemas.optimizaciones para las cuales la condición para un extremo local es una inversión de la derivada de la función a 0. En otras palabras, dicho problema puede reducirse a encontrar las raíces de la ecuación p (x) = 0, donde p (x) es idéntico a g "(x).
Para algunos tipos de ecuaciones no lineales,por ejemplo, trigonométrico cuadrado o simple, puede encontrar las raíces de maneras bastante simples. En particular, cada alumno conoce las fórmulas, con las cuales puede encontrar fácilmente los valores de los argumentos de los puntos donde el trinomio cuadrado se pone a cero.
Métodos para extraer las raíces de ecuaciones no lineales.Se acostumbra dividir en analítico (directo) e iterativo. En el primer caso, la solución deseada tiene la forma de una fórmula, usando la cual para varias operaciones aritméticas se puede encontrar el valor de las raíces deseadas. Se desarrollan métodos similares para ecuaciones exponenciales, trigonométricas, logarítmicas y algebraicas más simples. Por lo demás, se deben utilizar métodos numéricos especiales. Son fáciles de implementar usando computadoras que le permiten encontrar las raíces con la precisión requerida.
Entre ellos se encuentra el llamado método numérico de tangentes. Este último fue propuesto por el gran científico Isaac Newton a fines del siglo XVII. En siglos posteriores, el método fue mejorado repetidamente.
Численные способы решения сложных уравнений, не teniendo decisiones analíticas, se acostumbra llevar a cabo en 2 etapas. Primero necesitas localizarlos. Esta operación consiste en encontrar dichos segmentos en OX en los que hay una raíz de la ecuación que se está resolviendo.
Considere el segmento [a, b].Si g (x) no tiene espacios en blanco y toma valores de diferentes signos en los puntos finales, entonces al menos 1 raíz de la ecuación g (x) = 0 se encuentra entre a y b o en ellos mismos. Para que sea único, se requiere que g (x) en [a, b] fue monótono. Como saben, poseerá esta propiedad bajo la condición del signo constante g '(x).
En otras palabras, si en [a, b] g (x) no tiene discontinuidades y aumenta o disminuye monotónicamente, y sus valores en los puntos finales no tienen los mismos signos, entonces en [a, b] hay 1 y solo 1 raíz g (x )
Cabe señalar que este criterio no se aplicará a las raíces de las ecuaciones que son múltiples.
Antes de considerar métodos numéricos más complejos (método tangente y sus variedades) vale la pena conocerLa forma más fácil de identificar las raíces. Se llama dicotomía y se refiere a métodos intuitivos. El algoritmo de búsqueda de raíz se basa en el teorema de que si para g (x) continua en [x0, x1] se cumple la condición de signo diferente, luego en el segmento considerado hay al menos 1 raíz g (x) = 0.
Para detectarlo, debe dividir el segmento [x0, x1] por la mitad y marque el punto medio como x2. Entonces son posibles dos opciones: g (x0) * g (x2) o g (x2) * g (x1) son iguales o menores que 0. Elija uno para el cual una de estas desigualdades sea verdadera. Repita el procedimiento descrito anteriormente hasta la longitud [x0, x1] no será inferior a un cierto valor preseleccionado que determina la precisión de determinar la raíz de la ecuación en [x0, x1tu
Las ventajas del método incluyen su fiabilidad ysimplicidad, y el inconveniente es la necesidad de identificar inicialmente los puntos en los que g (x) toma diferentes signos, por lo que no se puede usar para raíces con incluso multiplicidad. Además, no generaliza el caso de un sistema de ecuaciones o si estamos hablando de raíces complejas.
Supongamos que queremos resolver la ecuación g (x) = 2x5 + x - 1 = 0.Para no buscar un segmento adecuado durante mucho tiempo, creamos un programa utilizando, por ejemplo, el famoso programa Excel. Vemos que como un segmento para la localización de la raíz es mejor tomar valores del intervalo [0,1]. Podemos estar seguros de que al menos una raíz de la ecuación deseada está en ella.
g "(x) = 10x4 + 1, es decir, es una función monotónicamente creciente, por lo tanto, solo hay 1 raíz en el segmento seleccionado.
Sustituimos los puntos finales en la ecuación.Tenemos 0 y 1, respectivamente. En el primer paso, tomamos el punto 0.5 para la solución. Entonces g (0.5) = -0.4375. Entonces, el siguiente segmento para reducir a la mitad será [0.5, 1]. Su punto medio es 0,75. En ella, el valor de la función es 0.226. Tomamos en consideración el segmento [0.5, 0.75] y su centro, que se encuentra en 0.625. Calculamos el valor de g (x) en 0.625. Es -0.11, es decir, negativo. En base a este resultado, seleccionamos el segmento [0.625, 0.75]. Obtenemos x = 0.6875. Entonces g (x) = -0.00532. Si la precisión de la solución es 0.01, entonces podemos suponer que el resultado deseado es 0.6875.
Este método de encontrar raíces por el método tangente de Newton es popular debido a su convergencia muy rápida.
Se basa en el hecho comprobado de que si xSr. - aproximación a la raíz f (x) = 0 tal que f "C1, entonces la próxima aproximación será en el punto donde la ecuación de la tangente a f (x) se pone a cero, es decir

Sustituir x = xn + 1 y anular y.
Entonces el algoritmo del método tangente se ve así:

Intentemos utilizar el método clásico de la tangente de Newton y encontrar una solución para alguna ecuación no lineal que sea difícil o imposible de encontrar analíticamente.
Supongamos que necesitamos identificar las raíces para x3 + 4x - 3 = 0 con cierta precisión, por ejemplo0.001. Como saben, la gráfica de cualquier función en forma de polinomio de grado impar debe cruzar al menos una vez el eje OX, es decir, no hay duda de que las raíces existen.
Antes de resolver nuestro ejemplo por el método tangente, trazamos f (x) = x3 + 4x - 3 puntiagudos. Esto es muy fácil de hacer, por ejemplo, usando el procesador de hojas de cálculo Excel. Del gráfico obtenido se verá que en [0,1] se cruza con el eje OX y la función y = x3 + 4x - 3 aumenta de forma monótona. Podemos estar seguros de que en [0,1] las ecuaciones x3 + 4x - 3 = 0 tiene una solución y es única.
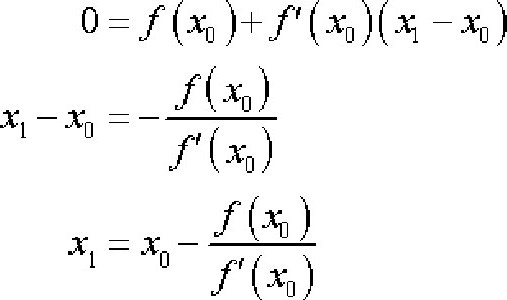
Cualquier solución de las ecuaciones por el método tangente comienza con el cálculo de f "(x). Tenemos:
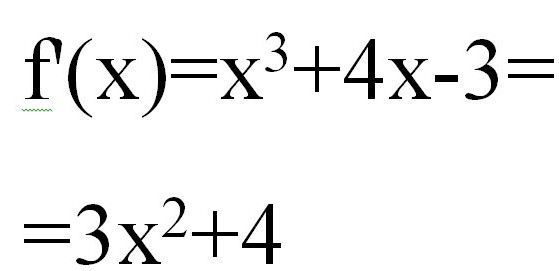
Entonces la segunda derivada tendrá la forma x * 6.
Usando estas expresiones, podemos escribir una fórmula para identificar las raíces de la ecuación por el método tangente en la forma:

A continuación, debe elegir la aproximación inicial, es decir, para tratar de determinar qué punto se considera el punto de partida (vol. X0) para el proceso iterativo. Consideramos los extremos del segmento [0,1]. Aquel para el cual la condición de la diversidad de la función y su segunda derivada en x0. Como puede ver, al sustituir x0 = 0 está roto, pero x0 = 1 es bastante adecuado.
Entonces como

entonces, si estamos interesados en la solución por el método tangente con precisión e, entonces el valor xSr. puede considerarse que satisface los requisitos del problema, siempre que la desigualdad | f (xSr.) / f ’(xSr.) | En el primer paso para resolver el problema por el método tangente, tenemos: El ejemplo anterior se puede resolver de manera mucho más fácil y rápida si no realiza los cálculos manualmente (en una calculadora), pero usa las capacidades de un procesador de mesa de Microsoft. Para hacer esto, en "Excel" necesita crear una nueva página y llenar sus celdas con las siguientes fórmulas: A continuación, debe "estirar" las fórmulas en las columnas C, D y E, primero en dos filas, y después de que aparezcan los valores en ellas, haga lo mismo con la columna B. En una tarea específica, ya en la celda B10 aparecela inscripción "Finalización de iteraciones", y para resolver el problema deberá tomar el número escrito en la celda ubicada una línea arriba. Para ello, se puede distinguir una columna "estirable" separada mediante la introducción de una fórmula condicional según la cual el resultado se escribirá allí si el contenido de una u otra celda de la columna B toma la forma "Finalización de iteraciones". Intentemos obtener una solución a la ecuación no lineal y = x4 - 4 - 2 * x por el método tangente en Pascal. Используем вспомогательную функцию, которая ayudará a realizar un cálculo aproximado f "(x) = (f (x + delta) - f (x)) / delta. Como condición para completar el proceso iterativo, elegimos la desigualdad | x0con1| El programa es notable porque no requiere el cálculo manual de la derivada. Considere otra forma de identificar las raíces.ecuaciones no lineales. El proceso de iteración consiste en el hecho de que, como aproximaciones sucesivas a la raíz deseada para f (x) = 0, tomamos los valores de los puntos de intersección del acorde con las abscisas de los puntos finales ayb con OX, denotado por x1, ..., xSr. . Tenemos:
El método tangente en Excel
Implementación de Pascal

Método de acordes
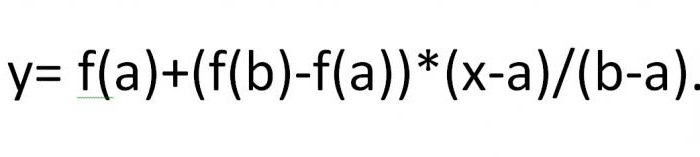
Para el punto donde el acorde se cruza con el eje OX, la expresión se escribe como:

Deje que la segunda derivada sea positiva para x £ [a, b] (el caso opuesto se reduce al considerado, si escribimos –f (x) = 0). En este caso, el gráfico y = f (x) es una curva convexa debajo y ubicada debajo del acorde Ab. Puede haber 2 casos: cuando la función tiene un valor positivo en el punto a o es negativa en el punto b.
En el primer caso, como el fijo, elija el final de a, y para x0 tomar el punto b. Luego, las aproximaciones sucesivas mediante la fórmula presentada anteriormente forman una secuencia que disminuye monotónicamente.
En el segundo caso, el extremo b se fija en x0 = a. Los valores de x obtenidos en cada paso de la iteración forman una secuencia que aumenta monotónicamente.
Por lo tanto, podemos afirmar que:
Las iteraciones pueden continuar hasta las condiciones para la proximidad de las raíces en este y el paso iterativo anterior módulo abs (xm - xm - 1) 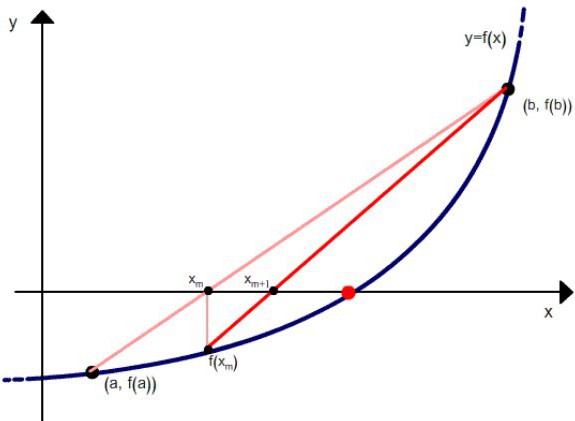
Método combinado de acordes y tangentes le permite establecer las raíces de la ecuación,acercándolos desde diferentes ángulos. Tal valor en el cual el gráfico f (x) cruza OX nos permite refinar la solución mucho más rápido que para cada uno de los métodos individualmente.
Supongamos que necesitamos encontrar las raíces f (x) = 0 siestán en [a, b]. Puede aplicar cualquiera de los métodos descritos anteriormente. Sin embargo, es mejor probar una combinación de ellos, lo que aumentará significativamente la precisión de la raíz.
Consideramos el caso con una aproximación inicial correspondiente a la condición de la diversidad de la primera y segunda derivada en un punto específico x.
Bajo tales condiciones, la solución de ecuaciones no lineales por el método tangente permite encontrar la raíz con un exceso si x0= b, y el método que usa acordes con el extremo fijo de b conduce a encontrar una raíz aproximada con una desventaja.
Se utilizan las siguientes fórmulas:

Ahora, la raíz x deseada debe buscarse en el intervalo [a1b1] En el siguiente paso, debe aplicar el método combinado ya a este segmento. Actuando así, obtenemos fórmulas de la forma:

Si hay una diferencia en la primera y segunda derivada, entonces, razonando de manera similar, para aclarar la raíz, obtenemos las siguientes fórmulas de recurrencia:

Como condición, la desigualdad estimada | bSr.+1 - unSr.+1| Si la desigualdad anterior es verdadera, entonces encomo la raíz de la ecuación no lineal en un segmento dado, tome un punto que esté exactamente en el medio entre las soluciones encontradas en un paso iterativo particular. El método combinado se implementa fácilmente en el entorno TURBO PASCAL. Si lo desea, puede intentar realizar todos los cálculos utilizando el método tabular en el programa Excel. En el último caso, se seleccionan varias columnas para resolver el problema utilizando acordes y por separado para el método propuesto por Isaac Newton. При этом каждая строка используется для записи cálculos en un paso iterativo específico utilizando dos métodos. Luego, en el lado izquierdo del área de solución, en la página de trabajo activa, se resalta una columna en la que se ingresa el resultado del cálculo del módulo de la diferencia en los valores del siguiente paso iterativo para cada método. Otro puede usarse para ingresar los resultados de los cálculos de acuerdo con la fórmula de cálculo del constructo lógico “IF”, usado para determinar si la condición se cumple o no.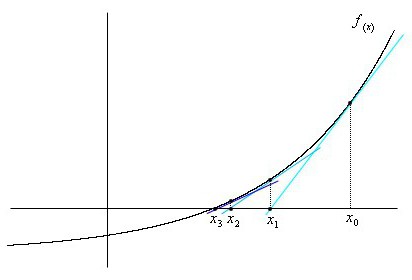
Ahora sabes cómo resolver ecuaciones complejas. Método tangente Como ya ha visto, se implementa de manera bastante simple, tanto en Pascal como en Excel. Por lo tanto, siempre puede establecer las raíces de una ecuación que es difícil o imposible de resolver mediante fórmulas.


























