
La historia del estudio de la radiactividad comenzó el 1 de marzo.1896, cuando el famoso científico francés Henri Becquerel descubrió accidentalmente la extrañeza en la emisión de sales de uranio. Resultó que las placas fotográficas ubicadas en la misma caja con la muestra están iluminadas. Una extraña radiación altamente penetrante, que poseía el uranio, condujo a esto. Esta propiedad se encontró en los elementos más pesados que completan la tabla periódica. Se le dio el nombre de "radiactividad".
Este proceso es la transformación espontánea.átomo de un isótopo de un elemento en otro isótopo con liberación simultánea de partículas elementales (electrones, núcleos de átomos de helio). La transformación de los átomos resultó ser espontánea, no requiriendo la absorción de energía del exterior. La cantidad principal que caracteriza el proceso de liberación de energía durante la desintegración radiactiva se denomina actividad.
A = λN, donde λ es la constante de descomposición, N es el número de átomos activos en la muestra.
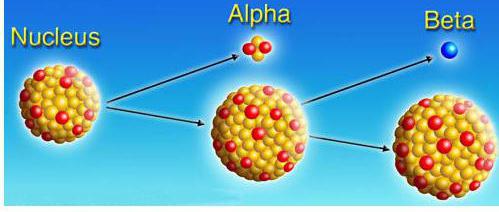
Asignar α, β, γ-desintegraciones. Las ecuaciones correspondientes se llaman reglas de desplazamiento:
el nombre | Que pasa | Ecuación de reacción |
a -decay | La transformación del núcleo atómico X en el núcleo de Y con la separación del núcleo del átomo de helio. | HAX→Z-2YA-4+2No4 |
β - desintegración | La transformación del núcleo atómico X en el núcleo Y con la liberación de un electrón. | HAX→Z + 1YA+-1eA |
γ - desintegración | no acompañado por un cambio en el núcleo, la energía se libera en forma de una onda electromagnética | HXA→HConA+ γ |
El momento del colapso de las partículas no se puede configurar paraeste átomo en particular. Para él, es más un "accidente" que un patrón. La liberación de energía que caracteriza este proceso se define como la actividad de la muestra.

Se establece que hay un tiempo paraque exactamente la mitad de los átomos de esta muestra sufre decaimiento. Este intervalo de tiempo se llama la "vida media". ¿Cuál es el significado de la introducción de este concepto?
Parece que por un tiempo igual al períodoexactamente la mitad de todos los átomos activos de una muestra determinada en descomposición. Pero, ¿significa esto que en el tiempo de dos vidas medias todos los átomos activos se desintegrarán completamente? En absoluto Después de un cierto momento, la mitad de los elementos radiactivos permanecen en la muestra, después de la otra mitad de los átomos restantes, la mitad de los átomos restantes, y así sucesivamente. En este caso, la radiación persiste durante mucho tiempo, mucho más que la vida media. Esto significa que los átomos activos se almacenan en la muestra independientemente de la radiación.
La vida media es un valor que depende únicamente de las propiedades de una sustancia determinada. La magnitud de la magnitud se determina para muchos isótopos radiactivos conocidos.
| Título | Notación | Tipo de decaimiento | Vida media |
Radio | 88Ra219 | alfa | 0.001 segundos |
Magnesio | 12Mg27 | beta | 10 minutos |
Radón | 86Ph222 | alfa | 3.8 días |
Cobalto | 27Con60 | gamma beta | 5.3 años |
Radio | 88Ra226 | alfa gamma | 1620 años |
Uranio | 92Tener238 | alfa gamma | 4.5 mil millones de años |
Vida media determinadaexperimentalmente En el curso de estudios de laboratorio, la actividad se mide repetidamente. Dado que las muestras de laboratorio son de tamaño mínimo (la seguridad del investigador es primordial), el experimento se realiza con un intervalo de tiempo diferente, repetido muchas veces. Se basa en el patrón de cambio en la actividad de las sustancias.
Para determinar la vida media.La actividad de esta muestra se mide en intervalos de tiempo específicos. Teniendo en cuenta el hecho de que este parámetro está asociado con el número de átomos en descomposición, la ley de la desintegración radiactiva determina la vida media.

Deje que el número de elementos activos del isótopo estudiado en un momento dado sea N, el intervalo de tiempo durante el cual se realiza la observación t2- t1donde los puntos de inicio y final de la observación están lo suficientemente cerca. Supongamos que n es el número de átomos que se desintegran en un intervalo de tiempo dado, entonces n = KN (t2- t1)
En esta expresión, K = 0.693 / T½ es el coeficiente de proporcionalidad, que se llama constante de decaimiento. T½ es la vida media del isótopo.
Tome el intervalo de tiempo para la unidad. En este caso, K = n / N indica la fracción de los núcleos de isótopos presentes, que decaen por unidad de tiempo.
Conociendo el valor de la constante de descomposición, se puede determinar la vida media de la descomposición: T½ = 0.693 / K.
De esto se deduce que, por unidad de tiempo, no un cierto número de átomos activos, sino una cierta proporción de ellos, decae.
Период полураспада положен в основу ЗРР.Frederico Soddy y Ernest Rutherford derivan el patrón basándose en los resultados de estudios experimentales en 1903. Es sorprendente que las mediciones repetidas realizadas con la ayuda de instrumentos lejos de ser perfectos, en las condiciones de principios del siglo XX, conduzcan a un resultado preciso y razonable. Se convirtió en la base de la teoría de la radioactividad. Derivamos un registro matemático de la ley de decaimiento radiactivo.

- Deje N0 - El número de átomos activos en un momento dado. Después de que el intervalo de tiempo t expire, los elementos N permanecerán intactos.
- En el momento en que sea igual a la vida media, exactamente la mitad de los elementos activos permanecerán: N = N0/ 2.
- Después de otra semivida en la muestra permanece: N = N0/ 4 = N0/ 22 átomos activos.
- Después de un período de tiempo igual a otra vida media, la muestra solo se guardará: N = N0/ 8 = N0/ 23.
- En el momento en que n pasan las vidas medias, N = N permanecerá en la muestra0/ 2Sr. partículas activas. En esta expresión, n = t / T½: la relación entre el tiempo del estudio y la vida media.
- ЗРР tiene una expresión matemática ligeramente diferente, más conveniente para resolver problemas: N = N02-t / T½.
Закономерность позволяет определить, помимо vida media, el número de átomos de isótopos activos que no se han descompuesto en un momento dado. Al saber la cantidad de átomos de la muestra al comienzo de la observación, después de un tiempo, puede determinar la vida útil de este medicamento.
La fórmula para la ley de la desintegración radiactiva ayuda a determinar la vida media solo si hay ciertos parámetros: el número de isótopos activos en la muestra, que es difícil de reconocer.
Escriba la fórmula ZRR posible, utilizando el concepto de actividad y la masa de los átomos del fármaco.
La actividad es proporcional al número de átomos radiactivos: A = A0• 2-t / t. En esta formula a0 - actividad de la muestra en el momento inicial, A - actividad después de t segundos, T - vida media.
La masa de una sustancia se puede usar en regularidad: m = m0• 2-t / t
Durante períodos iguales de tiempo, exactamente la misma proporción de átomos radiactivos presentes en esta preparación decae.
La ley en todos los sentidos es estadística,Determinando los procesos que ocurren en el micromundo. Está claro que la vida media de los elementos radiactivos es un valor estadístico. La naturaleza probabilística de los eventos en los núcleos atómicos sugiere que un núcleo arbitrario puede colapsarse en cualquier momento. Es imposible predecir un evento, solo se puede determinar su probabilidad en un momento dado. Como consecuencia, la vida media no tiene sentido:

Существование атома в его первоначальном La condición puede durar un segundo, y tal vez millones de años. Hablar sobre la vida útil de esta partícula tampoco es necesario. Introduciendo un valor igual al valor promedio de la vida útil de los átomos, podemos hablar de la existencia de átomos de un isótopo radioactivo, las consecuencias de la desintegración radiactiva. La vida media de un núcleo atómico depende de las propiedades de un átomo dado y no depende de otras cantidades.
¿Es posible resolver el problema: cómo encontrar la vida media, conociendo la vida media?
Para determinar la vida media, la fórmula de relación entre la vida media de un átomo y la disminución constante no ayuda menos.
τ = T1/2/ ln2 = T1/2/ 0.693 = 1 / λ.
En este registro, τ es el tiempo de vida promedio, λ es la constante de decaimiento.
El uso de ZRR para determinar la edad del individuoLas muestras se generalizaron en estudios de finales del siglo XX. La precisión para determinar la edad de los artefactos fósiles ha aumentado tanto que puede dar una idea de la época de la vida en los milenios antes de Cristo.
Análisis de radiocarbono de fósiles orgánicos.Las muestras se basan en cambios en la actividad del carbono-14 (un isótopo de carbono radiactivo) presente en todos los organismos. Entra en un organismo vivo en el proceso del metabolismo y está contenido en una cierta concentración. Después de la muerte, el metabolismo con el medio ambiente se detiene. La concentración de carbono radioactivo disminuye debido a la descomposición natural, la actividad disminuye proporcionalmente.
Si existe un valor como la vida media, la fórmula de la ley de la desintegración radioactiva ayuda a determinar el tiempo desde el momento de la terminación de la actividad vital del organismo.

Se realizaron estudios de radiactividad enCondiciones de laboratorio. La sorprendente capacidad de los elementos radiactivos para permanecer activos durante horas, días e incluso años no pudo dejar de sorprender a los físicos a principios del siglo XX. La investigación, por ejemplo, el torio, fue acompañada por un resultado inesperado: en un frasco cerrado, su actividad fue significativa. Al menor aliento, ella se cayó. La conclusión fue simple: la transformación del torio se acompaña de la liberación de radón (gas). Todos los elementos en el proceso de la radiactividad se transforman en una sustancia completamente diferente, que difiere en propiedades físicas y químicas. Esta sustancia, a su vez, también es inestable. Actualmente, hay tres series de transformaciones similares.
El conocimiento de tales transformaciones es extremadamente importante cuandodeterminar el tiempo de inaccesibilidad de las zonas contaminadas durante investigaciones atómicas y nucleares o catástrofes. La vida media del plutonio, dependiendo de su isótopo, está en el intervalo de 86 años (Pu 238) a 80 millones de años (Pu 244). La concentración de cada isótopo da una idea del período de descontaminación del territorio.
Se sabe que en nuestro tiempo hay metales.Mucho más caro que el oro, la plata y el platino. Estos incluyen el plutonio. Curiosamente, el plutonio creado en el curso de la evolución no se produce en la naturaleza. La mayoría de los elementos obtenidos en el laboratorio. La operación de plutonio-239 en reactores nucleares ha permitido que se vuelva extremadamente popular en estos días. La obtención de una cantidad de este isótopo suficiente para su uso en reactores hace que sea prácticamente invaluable.

Plutonio-239 se obtiene in vivocomo consecuencia de la cadena de transformaciones de uranio-239 a neptunio-239 (vida media - 56 horas). Una cadena similar le permite acumular plutonio en reactores nucleares. La tasa de ocurrencia de la cantidad requerida excede la natural en mil millones.
Можно много говорить о недостатках атомной La energía y la "extrañeza" de la humanidad, que prácticamente cualquier descubrimiento utiliza para destruir a su propia especie. El descubrimiento del plutonio-239, que puede participar en una reacción en cadena nuclear, ha permitido que se use como fuente de energía pacífica. El uranio-235, que es un análogo del plutonio, es extremadamente raro en la Tierra; es mucho más difícil aislarlo del mineral de uranio que obtener plutonio.
El análisis de radioisótopos de isótopos radiactivos proporciona una imagen más precisa de la vida útil de una muestra.
Utilizando la cadena de transformaciones "uranio - torio",Contenida en la corteza, permite determinar la edad de nuestro planeta. El porcentaje de estos elementos en promedio a lo largo de la corteza es la base de este método. Según los últimos datos, la edad de la Tierra es de 4.600 millones de años.


























