
삼각형은 평면 측정의 기본 수치 중 하나입니다.학교 교과 과정에서 그와 함께 실제, 어떤 의미에서 기하학에 대한 연구가 시작됩니다. 모서리 유형에 따라이 유형의 그림은 여러 유형으로 나눌 수 있습니다. 문제를 해결할 때 가장 쉬운 방법은 일반적으로 직사각형으로 간주됩니다. 그에게는 많은 이론, 규칙 및 삼각 함수가있어서 한쪽 또는 길이 (직선을 제외한 것)의 길이 만 알고 다리 또는 빗변을 찾을 수 있습니다.
그러나 그러한 종만이 존재한다면삼각형, 고등학생의 삶은 훨씬 간단하고 평온합니다. 그러나 이것은 그렇지 않습니다. 지오메트리 스터디는 각각의 특성과 특성을 가지고 있습니다. 자신있게 문제를 해결하려면 모든 다각형의 속성을 알아야합니다.

이등변 삼각형은 애완 동물과 매우 유사합니다소개에서 언급 된 피타고라스. 5 학년이라도 건설 또는 알 수없는 요소 찾기와 관련된 규칙을 이해합니다. 중요한 것은 기하학의 기본 개념과 평평한 그림의 기본 요소에 정통해야합니다.
이등변 삼각형의 속성이 나타남그것의 구조에서. 이러한 다각형의 밑면에있는 두 개의 각도는 측면과 동일합니다. 이 정보에서 즉시 명확한 결론을 도출 할 수 있습니다. 밑면의 모서리 중 하나를 알고 피크의 정도 측정을 찾으려면 2를 곱하고 180 °에서 빼야합니다. 극단 점이 상단과 하단에있는 양면을 측면이라고합니다.
이 수치에는 규칙이 없습니다.과제는 건축에서 비롯되어 학생들이 이해하고 편리하게 만듭니다. 그러나 이등변 삼각형의 중앙값 속성이라고 할 수있는 주요 기능이 하나 있습니다. 그것은 이중적 성격에 관한 것입니다. 모든 규칙에 따라 종이에 그러한 삼각형을 만들면 중앙의 선이 중간뿐만 아니라 높이와 이등분선임을 알 수 있습니다.
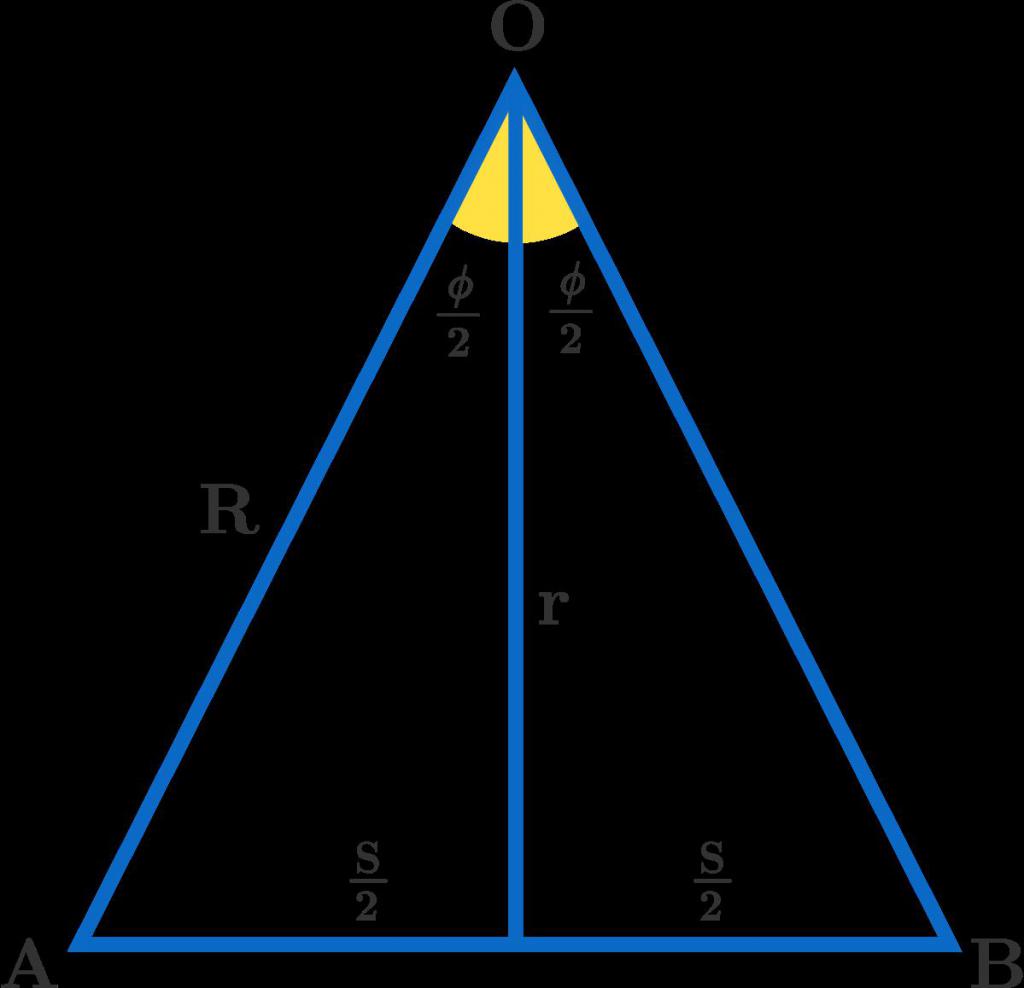
Прямая, которую проводят от вершины до основания, 너무 모호하지 않습니다. 그 특성은 이등변 삼각형의 주요 특징에 의해 결정됩니다. 정점의 모서리에서 밑면으로 내려 가면 두 개의 동일한 삼각형이 만들어지고 밑면과 같은 세그먼트로 나누는 수직선이 형성됩니다. 이 유형의 삼각형을 등변과 혼동해서는 안됩니다 (이러한 실수는 종종 학생들에 의해 이루어집니다). 여기에는 두 개가 아닌 세 개의 동일한 모서리가 있습니다.
