
O triângulo é um dos mais comunsformas geométricas, que conhecemos já na escola primária. Cada aluno enfrenta a questão de como encontrar a área de um triângulo nas aulas de geometria. Então, quais características de localização da área de uma determinada figura podem ser distinguidas? Neste artigo, veremos as fórmulas básicas necessárias para concluir essa tarefa e também analisaremos os tipos de triângulos.

Você pode encontrar a área de um triângulo de maneiras completamente diferentes, porque na geometria, mais de um tipo de forma é distinto, contendo três cantos. Esses tipos incluem:
Vamos dar uma olhada em cada um dos tipos existentes de triângulos.

Esta figura geométrica é considerada a maiscomum na resolução de problemas geométricos. Quando se torna necessário desenhar um triângulo arbitrário, essa opção vem em seu socorro.
Em um triângulo de ângulo agudo, como o nome indica, todos os ângulos são agudos e somam 180 °.
Este triângulo também é muito comum,no entanto, é encontrado um pouco menos freqüentemente em ângulo agudo. Por exemplo, ao resolver triângulos (ou seja, você conhece vários de seus lados e ângulos e precisa encontrar os elementos restantes), às vezes é necessário determinar se o ângulo é obtuso ou não. O cosseno de um ângulo obtuso é um número negativo.
Em um triângulo obtuso, um dos ângulos excede 90 °, de modo que os dois ângulos restantes podem assumir valores pequenos (por exemplo, 15 ° ou mesmo 3 °).
Para encontrar a área de um triângulo desse tipo, você precisa conhecer algumas das nuances, das quais falaremos mais adiante.
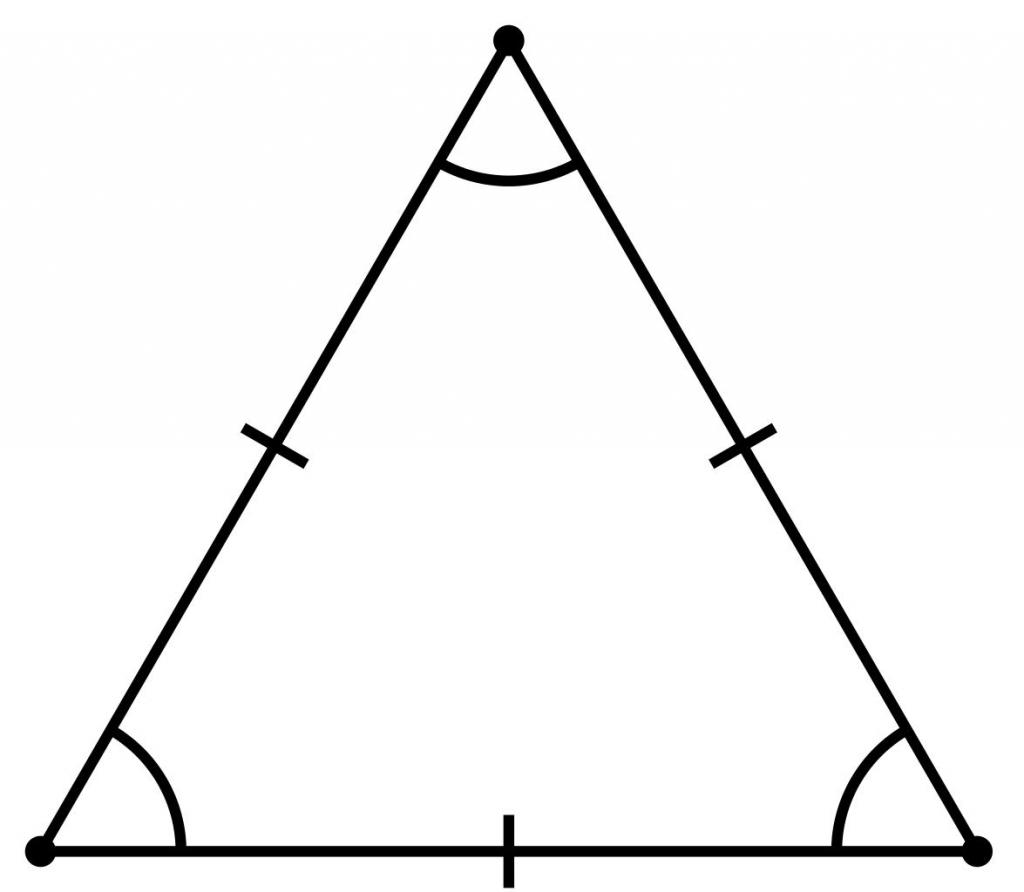
Um polígono regular é uma figuraincluindo n cantos, em que todos os lados e ângulos são iguais. Este é um triângulo regular. Como a soma de todos os ângulos do triângulo é 180 °, cada um dos três ângulos é 60 °.
Um triângulo regular, devido à sua propriedade, também é chamado de figura equilátero.
Também é importante notar que apenas um círculo pode ser inscrito em um triângulo regular, e apenas um círculo pode ser descrito em torno dele, e seus centros estão localizados em um ponto.

Além do tipo equilátero, também se pode distinguirum triângulo isósceles, ligeiramente diferente dele. Em tal triângulo, dois lados e dois ângulos são iguais um ao outro, e o terceiro lado (ao qual ângulos iguais são adjacentes) é a base.
A figura mostra um triângulo isósceles DEF, cujos ângulos D e F são iguais, e DF é a base.

Um triângulo retângulo recebe esse nome porque um de seus ângulos é reto, ou seja, é igual a 90 °. Os outros dois ângulos somam 90 °.
O maior lado desse triângulo, situado em um ângulo oposto de 90 °, é a hipotenusa, enquanto os outros dois lados são pernas. Para este tipo de triângulos, o teorema de Pitágoras é aplicável:
A soma dos quadrados dos comprimentos das pernas é igual ao quadrado do comprimento da hipotenusa.
A figura mostra um triângulo retângulo BAC com a hipotenusa AC e as pernas AB e BC.
Para encontrar a área de um triângulo com um ângulo reto, você precisa saber os valores numéricos de suas pernas.
Vamos passar para as fórmulas para encontrar a área desta figura.
Na geometria, duas fórmulas podem ser distinguidas, quesão adequados para localizar a área da maioria dos tipos de triângulos, nomeadamente triângulos de ângulo agudo, obtuso, regular e isósceles. Vamos analisar cada um deles.
Esta fórmula é universal paraencontrar a área da figura que estamos considerando. Para isso, basta saber o comprimento da lateral e o comprimento da altura desenhada por ela. A fórmula em si (metade do produto da base e a altura) é assim:
S = ½ * A * H,
onde A é o lado do triângulo dado e H é a altura do triângulo.

Por exemplo, para encontrar a área de um triângulo ACB de ângulo agudo, multiplique seu lado AB pela altura CD e divida o valor resultante por dois.
No entanto, nem sempre é fácil encontrar a áreatriângulo desta forma. Por exemplo, para usar esta fórmula para um triângulo obtuso, é necessário continuar um de seus lados e só então desenhar a altura dele.
Na prática, essa fórmula é usada com mais frequência do que outras.
Esta fórmula, como a anterior, é adequada parada maioria dos triângulos e em seu significado é uma consequência da fórmula para encontrar a área ao lado e a altura do triângulo. Ou seja, a fórmula considerada pode ser facilmente derivada da anterior. Seu texto é o seguinte:
S = ½ * sinO * A * B,
onde A e B são os lados do triângulo e O é o ângulo entre os lados A e B.
Lembre-se de que o seno de um ângulo pode ser visto em uma tabela especial com o nome do notável matemático soviético V.M. Bradis.
Agora, vamos passar para outras fórmulas que são adequadas apenas para tipos excepcionais de triângulos.
Além da fórmula universal, que inclui a necessidade de desenhar a altura em um triângulo, a área de um triângulo contendo um ângulo reto pode ser encontrada por suas pernas.
Portanto, a área de um triângulo contendo um ângulo reto é metade do produto de suas pernas, ou:
S = ½ * a * b,
onde aeb são as pernas de um triângulo retângulo.
Este tipo de formas geométricas difere porqueque sua área pode ser encontrada para o valor indicado de apenas um de seus lados (já que todos os lados de um triângulo regular são iguais). Assim, diante do problema "encontre a área de um triângulo quando os lados são iguais", você precisa usar a seguinte fórmula:
S = A2* 3/4,
onde A é o lado de um triângulo equilátero.
A última opção para encontrar a área de um triângulo é a fórmula de Heron. Para usá-lo, você precisa saber os comprimentos dos três lados da figura. A fórmula de Heron é semelhante a esta:
S = √p (p - a) (p - b) (p - c),
onde a, bec são os lados desse triângulo.
Às vezes, o problema é dado:"Área de um triângulo regular - encontre o comprimento de seu lado". Nesse caso, você precisa usar a fórmula já conhecida por nós para encontrar a área de um triângulo regular e derivar o valor do lado (ou seu quadrado) a partir dele:
UMA2 = 4S / √3.
Nos problemas do GIA em matemática, existem muitas fórmulas. Além disso, muitas vezes é necessário encontrar a área de um triângulo em papel quadriculado.
Neste caso, é mais conveniente desenhar a altura de um dos lados da figura, determinar seu comprimento pelas células e usar a fórmula universal para encontrar a área:
S = ½ * A * H.
Assim, depois de estudar as fórmulas apresentadas no artigo, você não terá problemas para encontrar a área de um triângulo de qualquer tipo.


























