
En triangel är en av huvudfigurerna för planimetri.Det är med honom i skolplanen att studien av verklig geometri börjar. Beroende på typen av hörn kan denna typ av figurer delas upp i flera typer. När man löser problem anses det enklaste vara rektangulärt. För honom finns det många teorem, regler, såväl som trigonometriska funktioner som gör att du kan hitta alla ben eller hypotenus, bara vet längden på en av sidorna och vinkeln (vilken som helst förutom den raka linjen).
Men om bara en sådan art fannstrianglar, livet för gymnasieelever och gymnasieelever skulle vara mycket enklare och sorglösa. Men det är inte så. Varje figur som geometri studerar har sina egna egenskaper och egenskaper. För att säkert lösa problem måste du känna till alla polygoner.

Isosceles triangeln är mycket lik husdjuretPythagoras, som nämndes i inledningen. Reglerna förknippade med dess konstruktion eller hitta okända element, till och med en femte klassning förstår. Det viktigaste är att navigera väl i de grundläggande begreppen geometri och de grundläggande elementen i platta figurer.
Egenskaperna för en likställt triangel framträderfrån dess struktur. De två vinklarna vid foten av en sådan polygon är desamma som sidorna. Omedelbart från denna information kan vi dra en viss slutsats. För att hitta graden av toppmåttet, känna till ett av basens hörn, måste du multiplicera den med två och subtrahera från 180 °. Två sidor, vars extrema punkter är uppe och ner, kallas sida.
Reglerna har som sådan inte denna siffra - allt iuppgifterna kommer från dess konstruktion, vilket gör det förståeligt och bekvämt för studenter. Det finns emellertid en huvudfunktion som kan kallas egenskapen för medianen i en likgilt triangel. Det handlar om hennes dubbla natur. Om du på papper bygger en sådan triangel enligt alla regler, kan du se att linjen i mitten inte bara är medianen utan också höjden och halvan.
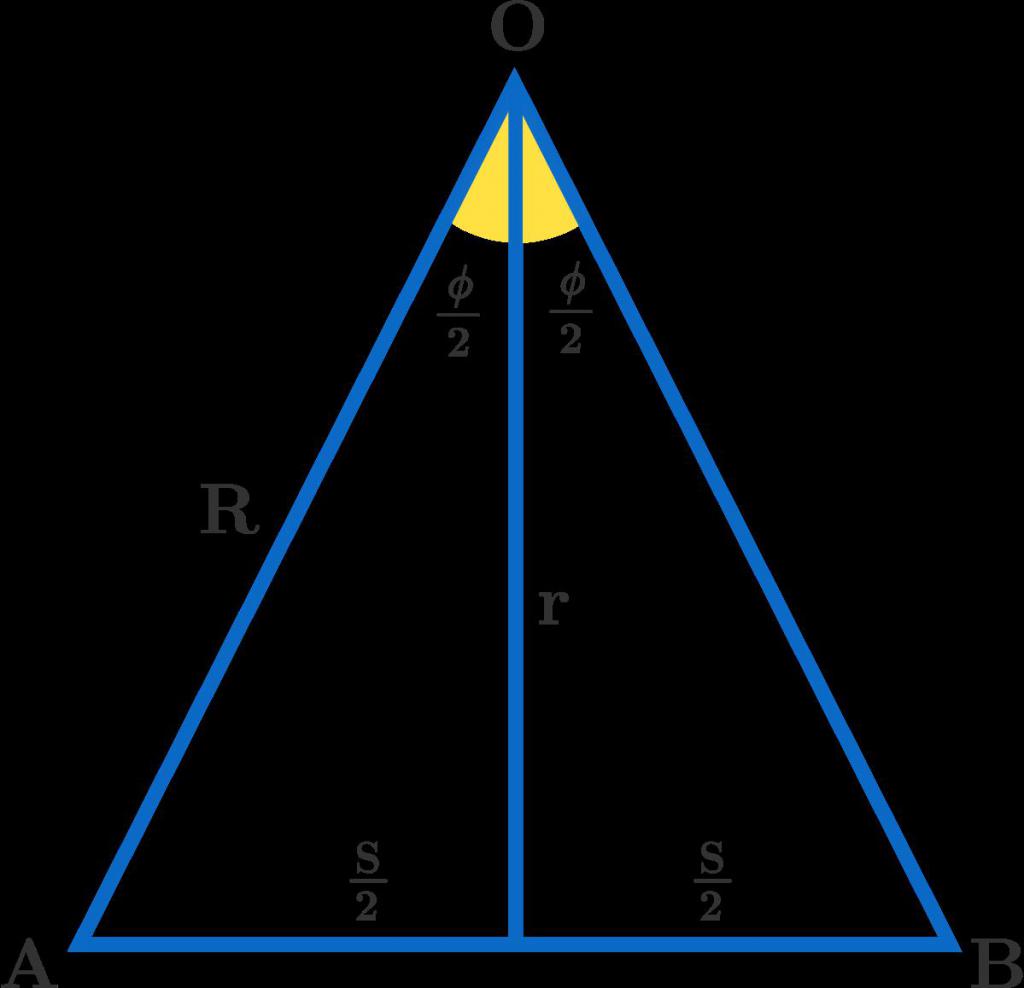
En linje ritad från toppen till botten,kommer inte att vara så entydig. Dess egenskaper bestäms av huvuddragen i en likställt triangel. Den släpps från hörnet av toppunkten till basen och skapar två lika stora trianglar, och med basen bildar en vinkelrätt, som delar upp den i lika segment. Denna typ av trianglar bör inte förväxlas med liksidiga trianglar (ofta gör ett sådant misstag av elever). De har tre identiska vinklar, och inte två, som här.


























