
कक्षा में समीकरणों को हल करने पर स्कूल में पीड़ागणितज्ञ, कई छात्र अक्सर यह सुनिश्चित करते हैं कि वे अपना समय पूरी तरह से बर्बाद कर रहे हैं, और फिर भी ऐसा कौशल जीवन में उपयोगी होगा न केवल उन लोगों के लिए जो डेसकार्टेस, यूलर या लोबचेवस्की के नक्शेकदम पर चलने का फैसला करते हैं।
व्यवहार में, उदाहरण के लिए चिकित्सा या अर्थशास्त्र में,काफी बार ऐसी परिस्थितियां होती हैं जब किसी विशेषज्ञ को यह पता लगाना होता है कि किसी विशेष दवा के सक्रिय पदार्थ की एकाग्रता रोगी के रक्त में आवश्यक स्तर तक पहुंच जाएगी या लाभदायक बनने के लिए किसी विशेष व्यवसाय के लिए आवश्यक समय की गणना करना आवश्यक है।
सबसे अधिक बार, हम nonlinear को हल करने के बारे में बात कर रहे हैंविभिन्न प्रकार के समीकरण। यह जितनी जल्दी हो सके, विशेष रूप से कंप्यूटर के उपयोग के साथ संख्यात्मक तरीकों की अनुमति देता है। वे अच्छी तरह से अध्ययन कर रहे हैं और लंबे समय तक प्रभावी साबित हुए हैं। उनमें से न्यूटन की स्पर्शरेखा विधि है, जिसके लिए यह लेख समर्पित है।

इस स्थिति में, एक फ़ंक्शन जी होता है, जो खंड (ए, बी) पर दिया जाता है और कुछ निश्चित मानों पर ले जाता है, अर्थात्, प्रत्येक (ए, बी) से संबंधित एक्स एक विशिष्ट संख्या जी (एक्स) से जुड़ा हो सकता है।
अंक ए और बी (सिरों सहित) के बीच अंतराल से समीकरण की सभी जड़ों को स्थापित करना आवश्यक है, जिसके लिए फ़ंक्शन शून्य है। जाहिर है, ये ओएक्स के साथ y = g (x) के प्रतिच्छेदन के बिंदु होंगे।
कुछ मामलों में, प्रपत्र जी के जी (x) = 0 को एक समान से बदलना अधिक सुविधाजनक है1(x) = जी2(एक्स)। इस मामले में, रेखांकन के प्रतिच्छेदन बिंदुओं के एब्सिसस (एक्स मान) जी1(x) और जी2(एक्स)।
ग़ैर-समतावादी समीकरण को हल करना भी समस्याओं के लिए महत्वपूर्ण हैअनुकूलन जिसके लिए स्थानीय चरम की स्थिति यह है कि फ़ंक्शन का व्युत्पन्न गायब हो जाता है। दूसरे शब्दों में, समीकरण p (x) = 0 की जड़ों को खोजने के लिए ऐसी समस्या को कम किया जा सकता है, जहां p (x) g "(x) के समान है।
कुछ प्रकार के नॉनलाइनियर समीकरणों के लिए,उदाहरण के लिए, वर्ग या सरल त्रिकोणमितीय, आप जड़ों को काफी सरल तरीकों से पा सकते हैं। विशेष रूप से, प्रत्येक छात्र सूत्रों को जानता है, जिसके उपयोग से कोई भी आसानी से उन बिंदुओं के तर्क के मूल्यों का पता लगा सकता है जहां वर्ग ट्रिनोमियल शून्य है।
Nonlinear समीकरणों की जड़ों को निकालने के लिए तरीकेयह विश्लेषणात्मक (प्रत्यक्ष) और पुनरावृत्त में विभाजित करने के लिए प्रथागत है। पहले मामले में, वांछित समाधान में एक सूत्र का रूप होता है, जिसका उपयोग करके, एक निश्चित संख्या में अंकगणितीय संचालन में, व्यक्ति वांछित जड़ों का मूल्य पा सकता है। इसी तरह के तरीकों को घातीय, त्रिकोणमितीय, लघुगणक और मूल बीजगणितीय समीकरणों के लिए विकसित किया गया है। बाकी के लिए, आपको विशेष संख्यात्मक विधियों का उपयोग करना होगा। वे कंप्यूटर का उपयोग करके लागू करना आसान है जो आवश्यक सटीकता के साथ जड़ों को खोजने की अनुमति देते हैं।
इनमें तथाकथित संख्यात्मक स्पर्शरेखा विधि शामिल है। बाद के महान वैज्ञानिक इसहाक न्यूटन द्वारा 17 वीं शताब्दी के अंत में प्रस्तावित किया गया था। निम्नलिखित शताब्दियों में, विधि में कई बार सुधार हुआ है।
जटिल समीकरणों को हल करने के लिए संख्यात्मक तरीके, नहींविश्लेषणात्मक समाधान होने के कारण, इसे 2 चरणों में किया जाता है। पहले आपको उन्हें स्थानीय बनाने की आवश्यकता है। इस ऑपरेशन में ओएक्स पर ऐसे सेगमेंट खोजने की सुविधा है, जिस पर समीकरण के एक रूट को हल किया जा रहा है।
सेगमेंट पर विचार करें [a, b]। यदि g (x) पर कोई रोक नहीं है और समापन बिंदुओं पर विपरीत संकेतों के मान लेता है, तो a और b के बीच या उनमें समीकरण g की कम से कम 1 जड़ है (x) = 0. अद्वितीय होने के लिए, यह आवश्यक है कि जी (एक्स) पर [ए, बी] एकरस था। जैसा कि ज्ञात है, इसके पास यह संपत्ति होगी, बशर्ते कि जी '(x) निरंतर संकेत का हो।
दूसरे शब्दों में, यदि [a, b] g (x) पर कोई असंतोष नहीं है और एकरूपता बढ़ती या घटती है, और समापन बिंदुओं पर इसके मान अलग-अलग हैं, तो [a, b] पर 1 मौजूद है और केवल 1 मूल g (x) है )।
उसी समय, आपको पता होना चाहिए कि यह मानदंड कई समीकरणों की जड़ों के लिए लागू नहीं होगा।
अधिक जटिल संख्यात्मक तरीकों पर विचार करने से पहले (स्पर्शरेखा विधि) और इसकी किस्में) इससे परिचित होने के लायक हैजड़ों की पहचान करने का सबसे आसान तरीका। इसे डाइकोटॉमी कहा जाता है और यह सहज तरीकों को संदर्भित करता है। जड़ों को खोजने के लिए एल्गोरिथ्म प्रमेय पर आधारित है कि अगर जी (x) के लिए [x पर निरंतर है0, एक्स1] विभिन्न संकेतों की स्थिति संतुष्ट है, तो माना अंतराल पर कम से कम 1 रूट जी (x) = 0 है।
इसे खोजने के लिए, आपको खंड [x को विभाजित करना होगा0, एक्स1] आधे में और x के रूप में मिडपॉइंट को चिह्नित करें2... फिर दो विकल्प संभव हैं: जी (एक्स0) * जी (एक्स2) या जी (एक्स2) * जी (एक्स1) के बराबर या कम से कम 0 हैं। इनमें से एक असमानता के लिए सही है। हम लंबाई [एक्स तक उपरोक्त प्रक्रिया दोहराते हैं0, एक्स1] कुछ निश्चित मूल्य से कम नहीं होगा जो समीकरण की जड़ को निर्धारित करने की सटीकता को निर्धारित करता है [x0, एक्स1]।
विधि के लाभों में इसकी विश्वसनीयता और शामिल हैंसादगी, और नुकसान शुरू में उन बिंदुओं की पहचान करने की आवश्यकता है जिन पर जी (x) अलग-अलग संकेत लेता है, इसलिए इसका उपयोग कई गुना के साथ जड़ों के लिए भी नहीं किया जा सकता है। इसके अलावा, यह समीकरणों की एक प्रणाली के मामले में या जब यह जटिल जड़ों की बात आती है, तो इसका सामान्यीकरण नहीं होता है।
मान लीजिए हम समीकरण g (x) = 2x को हल करना चाहते हैं5 + x - 1 = 0। लंबे समय तक एक उपयुक्त सेगमेंट की खोज न करने के लिए, हम एक ग्राफ का उपयोग करके निर्माण करते हैं, उदाहरण के लिए, प्रसिद्ध प्रोग्राम "एक्सेल"। हम देखते हैं कि रूट को स्थानीय बनाने के लिए एक खंड के रूप में अंतराल [0,1] से मान लेना बेहतर है। हम यह सुनिश्चित कर सकते हैं कि इसमें वांछित समीकरण की कम से कम एक जड़ हो।
g ”(x) = 10x4 + 1, अर्थात्, यह एक नीरस रूप से बढ़ता हुआ कार्य है, इसलिए चयनित खंड पर केवल 1 जड़ है।
समीकरण में समापन बिंदु को प्रतिस्थापित करें। हमारे पास क्रमशः 0 और 1 है। पहले चरण में, हम समाधान के लिए बिंदु 0.5 लेते हैं। फिर जी (0.5) = -0.4375। इसका मतलब यह है कि आधे हिस्से में विभाजित करने वाला अगला खंड [0,5, 1] होगा। इसका मध्यबिंदु 0.75 है। इसमें फ़ंक्शन मान 0.226 है। हम खंड [0.5, 0.75] और इसके मध्य को ध्यान में रखते हैं, जो कि बिंदु 0.625 पर है। 0.625 के जी (x) मान का मूल्यांकन करें। यह -0.11 के बराबर है, अर्थात नकारात्मक है। इस परिणाम के आधार पर, सेगमेंट [0.625, 0.75] का चयन करें। हमें x = 0.6875 मिलता है। फिर जी (एक्स) = -0.00532। यदि समाधान की सटीकता 0.01 है, तो हम मान सकते हैं कि वांछित परिणाम 0.6875 है।
न्यूटन की स्पर्शरेखा विधि का उपयोग करके जड़ों को खोजने की यह विधि अपने बहुत तेजी से अभिसरण के कारण लोकप्रिय है।
यह साबित तथ्य पर आधारित है कि यदि एक्सn - रूट एफ (एक्स) = 0 के लिए एक अनुमान है कि एफ "सी1, तो अगला सन्निकटन उस बिंदु पर होगा जहां स्पर्शरेखा का समीकरण f (x) शून्य है, अर्थात्।

पदार्थ x = xएन + १ और y को शून्य पर सेट करें।
फिर स्पर्शरेखा विधि एल्गोरिथ्म इस तरह दिखता है:

आइए शास्त्रीय न्यूटन स्पर्शरेखा विधि का उपयोग करने का प्रयास करें और कुछ गैर-रेखीय समीकरण का हल खोजें जो विश्लेषणात्मक रूप से खोजना मुश्किल या असंभव है।
इसे x के लिए जड़ों की पहचान करने की आवश्यकता है3 + 4x - 3 = 0 कुछ सटीक के साथ, उदाहरण के लिए0.001। जैसा कि आप जानते हैं, एक विषम डिग्री बहुपद के रूप में किसी भी फ़ंक्शन का ग्राफ कम से कम एक बार ओएक्स अक्ष को काटना चाहिए, अर्थात, जड़ों के अस्तित्व पर संदेह करने की कोई आवश्यकता नहीं है।
स्पर्शरेखा विधि का उपयोग करके हमारे उदाहरण को हल करने से पहले, हम एक ग्राफ बनाते हैं f (x) = x3 + 4x - 3 पॉइंटवाइज़। उदाहरण के लिए, एक्सेल स्प्रेडशीट का उपयोग करना बहुत आसान है। परिणामी ग्राफ से यह देखा जाएगा कि [0,1] पर यह OX अक्ष और फ़ंक्शन y = x के साथ प्रतिच्छेद करता है3 + 4x - 3 एकरस रूप से बढ़ता है। हम यह सुनिश्चित कर सकते हैं कि [0,1] समीकरण x पर3 + 4x - 3 = 0 का एक समाधान है और यह एकमात्र है।
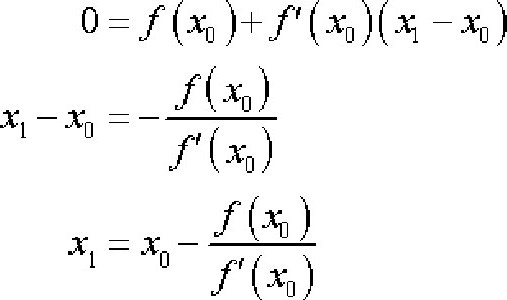
स्पर्शरेखा विधि द्वारा समीकरणों का कोई भी हल f (x) की गणना के साथ शुरू होता है। हमारे पास:
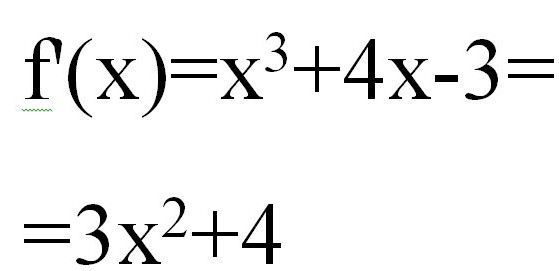
फिर दूसरे व्युत्पन्न में फॉर्म x * 6 होगा।
इन अभिव्यक्तियों का उपयोग करते हुए, हम फार्म में स्पर्शरेखा विधि का उपयोग करके समीकरण की जड़ों की पहचान करने के लिए सूत्र लिख सकते हैं:

अगला, आपको एक प्रारंभिक सन्निकटन चुनने की आवश्यकता है, अर्थात, यह निर्धारित करने के लिए कि कौन से बिंदु को प्रारंभिक बिंदु माना जाता है (ओ.बी.एस.0) पुनरावृति प्रक्रिया के लिए. खंड के छोर पर विचार करें [0,1]। एक वह जिसके लिए फ़ंक्शन की स्थिति और दूसरा एक्स में व्युत्पन्न है0... जैसा कि आप देख सकते हैं, जब x को प्रतिस्थापित किया जा रहा है0 = 0 का उल्लंघन किया जाता है, लेकिन एक्स0 = 1 ठीक है।
चूंकि

फिर अगर हम सटीकता ई के साथ स्पर्शरेखा की विधि द्वारा समाधान में रुचि रखते हैं, तो मूल्य एक्सn समस्या की आवश्यकताओं को संतोषजनक माना जा सकता है, बशर्ते कि असमानता। f (x)n) / एफ '(एक्स)n) | <ई।
स्पर्शरेखा विधि द्वारा समस्या को हल करने के पहले चरण में, हमारे पास:

यदि आप मैन्युअल रूप से (किसी कैलकुलेटर पर) परिकलन नहीं करते हैं, लेकिन Microsoft से एक स्प्रेडशीट प्रोसेसर की क्षमताओं का उपयोग करते हैं, तो पिछले उदाहरण को बहुत आसान और तेज़ हल किया जा सकता है।
ऐसा करने के लिए, एक्सेल में आपको एक नया पेज बनाने और निम्न फ़ार्मुलों के साथ इसकी कोशिकाओं को भरने की आवश्यकता है:
अगला, आपको कॉलम सी, डी और ई में सूत्र को "दो" करने की आवश्यकता है, पहले दो पंक्तियों द्वारा, और उनमें मान दिखाई देने के बाद, कॉलम बी के साथ भी ऐसा ही करें।
एक विशिष्ट कार्य में, पहले से ही सेल B10 दिखाई देगाशिलालेख "पुनरावृत्तियों का समापन", और समस्या को हल करने के लिए आपको एक पंक्ति में स्थित कक्ष में लिखी संख्या को लेना होगा। इसके लिए, आप वहां एक सशर्त सूत्र दर्ज करके एक अलग "विस्तार योग्य" कॉलम का चयन कर सकते हैं, जिसके अनुसार परिणाम वहां लिखा जाएगा यदि कॉलम बी के एक या दूसरे सेल में सामग्री "पुनरावृत्तियों का समापन" का रूप लेती है।
आइए नॉनलाइनियर समीकरण y = x का समाधान प्राप्त करने का प्रयास करें4 - 4 - 2 * x पास्कल में स्पर्शरेखा विधि द्वारा।
हम एक सहायक फ़ंक्शन का उपयोग करते हैं जोच की अनुमानित गणना करने में मदद करेगा "(x) = (f (x + डेल्टा) - f (x)) / डेल्टा। पुनरावृत्ति प्रक्रिया को पूरा करने के लिए एक शर्त के रूप में, हम असमानता की पूर्ति का चयन करते हैं। x0-एक्स1| <कुछ छोटी संख्या। पास्कल में, हम इसे एब्स (x0 - X1) <= एप्सिलॉन के रूप में लिखते हैं।
यह कार्यक्रम उल्लेखनीय है कि इसमें व्युत्पन्न की मैन्युअल गणना की आवश्यकता नहीं है।

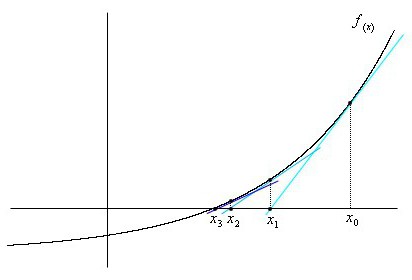
जड़ों की पहचान करने के दूसरे तरीके पर विचार करेंnonlinear समीकरण। पुनरावृत्ति प्रक्रिया है, च के लिए वांछित जड़ के लिए क्रमिक सन्निकटन (एक्स) = 0 के रूप में, अंत बिंदु के एबीसी के साथ फोर्किस के साथ कॉर्ड के प्रतिच्छेदन बिंदुओं के मूल्यों को लिया जाता है और एक्स के साथ बी लिया जाता है।1, ..., एक्सn ... हमारे पास है:
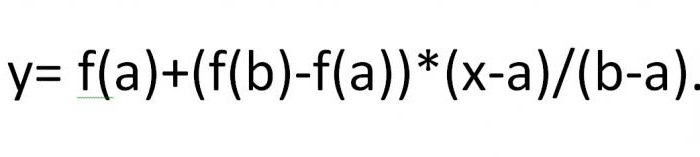
उस बिंदु के लिए जहां कॉर्ड OX अक्ष को काटता है, अभिव्यक्ति के रूप में लिखा जाएगा:

दूसरी व्युत्पत्ति को x £ [a, b] के लिए सकारात्मक होने दें (यदि हम लिखते हैं तो विपरीत मामले को घटा दिया जाएगा - f (x) = 0)। इस स्थिति में, ग्राफ y = f (x) नीचे की ओर एक वक्र उत्तल है और जीवा के नीचे स्थित है अब... 2 मामले हो सकते हैं: जब फ़ंक्शन का बिंदु पर सकारात्मक मूल्य होता है या बिंदु b पर नकारात्मक होता है।
पहले मामले में, हम अंत को एक निश्चित एक के रूप में चुनते हैं, और एक्स के लिए0 बिंदु बी ले लो। फिर उपर्युक्त सूत्र द्वारा क्रमिक सन्निकटन एक क्रम बनाते हैं जो एकरस रूप से घटता है।
दूसरे मामले में, अंतिम बिंदु बी x पर तय किया गया है0 = ए। प्रत्येक पुनरावृत्ति चरण पर प्राप्त x मान एक क्रम बनाते हैं जो एकरस रूप से बढ़ता है।
इस प्रकार, हम यह बता सकते हैं कि:
पुनरावृत्तियों को तब तक जारी रखा जा सकता है जब तक कि इस पर जड़ों की निकटता के लिए स्थितियां और पिछले पुनरावृत्ति चरण संतुष्ट नहीं हैं modulo abs (xम - एक्सम - 1) <ई।
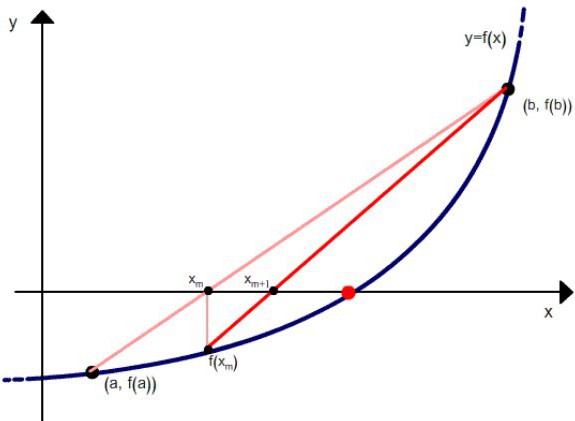
कॉर्ड और स्पर्शरेखा की संयुक्त विधि आपको समीकरण की जड़ें स्थापित करने की अनुमति देता है,विभिन्न पक्षों से उन्हें संपर्क करना। ऐसा मान जिस पर ग्राफ़ f (x) OX को पार करता है, आपको अलग-अलग तरीकों में से प्रत्येक के लिए समाधान को बहुत तेज़ी से परिष्कृत करने की अनुमति देता है।
मान लीजिए कि आपको जड़ों को खोजने की जरूरत है f (x) = 0 ifवे [ए, बी] पर हैं। आप ऊपर वर्णित किसी भी विधि को लागू कर सकते हैं। हालांकि, उनमें से एक संयोजन की कोशिश करना बेहतर है, जो रूट की सटीकता को बहुत बढ़ाएगा।
इस स्थिति के अनुसार एक प्रारंभिक सन्निकटन के साथ मामले पर विचार करें कि पहले और दूसरे डेरिवेटिव में एक विशेष बिंदु x पर अलग-अलग संकेत हैं।
ऐसी स्थितियों के तहत, स्पर्शरेखा विधि द्वारा गैर-समांतर समीकरणों को हल करने से एक्स के साथ एक अतिरिक्त के साथ एक रूट खोजने की अनुमति मिलती है0= b, और निश्चित अंत b के साथ जीवा का उपयोग करने की विधि एक कमी के साथ एक अनुमानित जड़ खोजने की ओर ले जाती है।
सूत्र उपयोग किए जाते हैं:

अब आवश्यक रूट x को अंतराल [a] में मांगा जाना चाहिए1, बी1]। अगला कदम इस सेगमेंट में संयुक्त विधि लागू करना है। ऐसा करने पर, हमें फॉर्म के सूत्र मिलते हैं:

यदि पहले और दूसरे डेरिवेटिव के संकेतों में अंतर होता है, तो, इसी तरह से बहस करते हुए, रूट को परिष्कृत करने के लिए, हम निम्नलिखित पुनरावर्ती सूत्र प्राप्त करते हैं:

अनुमानित असमानता | खn+1 - एn+1| <ई। दूसरे शब्दों में, व्यवहार में, आपको दो तरीकों का उपयोग करके एक समाधान ढूंढना होगा, लेकिन प्रत्येक चरण में आपको यह पता लगाना होगा कि परिणाम एक-दूसरे के कितने करीब हैं।
यदि उपरोक्त असमानता सत्य है, तो अंदरकिसी दिए गए सेगमेंट पर नॉनलाइनियर समीकरण की जड़ के रूप में, हम एक बिंदु लेते हैं जो किसी विशेष पुनरावृत्ति चरण में पाए जाने वाले समाधानों के बीच बिल्कुल बीच में होता है।
संयुक्त विधि आसानी से टर्बो पर्यावरण में कार्यान्वित की जाती है। यदि आप चाहते हैं, तो आप एक्सेल प्रोग्राम में सारणीबद्ध विधि से सभी गणना करने की कोशिश कर सकते हैं।
बाद के मामले में, कई स्तंभों को जीवाओं के उपयोग से समस्या को हल करने के लिए और इसहाक न्यूटन द्वारा प्रस्तावित विधि के लिए अलग से चुना जाता है।
इसके अलावा, प्रत्येक पंक्ति का उपयोग लिखने के लिए किया जाता हैदो तरीकों से एक विशिष्ट पुनरावृत्ति कदम पर गणना। फिर, समाधान क्षेत्र के बाईं ओर, सक्रिय कार्य पृष्ठ पर, एक कॉलम हाइलाइट किया जाता है, जिसमें प्रत्येक तरीकों के लिए अगले पुनरावृत्ति कदम के मूल्यों के बीच अंतर के मापांक की गणना करने का परिणाम दर्ज किया जाता है। तार्किक संरचना "आईएफ" की गणना के लिए सूत्र के अनुसार गणना के परिणामों को दर्ज करने के लिए एक और एक का उपयोग किया जा सकता है, यह पता लगाने के लिए इस्तेमाल किया जाता है कि क्या कोई शर्त पूरी हुई है या नहीं।
अब आप जानते हैं कि जटिल समीकरणों को कैसे हल किया जाए। स्पर्शरेखा विधि, जैसा कि आप पहले ही देख चुके हैं, यह पास्कल और एक्सेल दोनों में लागू करने के लिए काफी सरल है। इसलिए, आप हमेशा एक समीकरण की जड़ों को स्थापित कर सकते हैं जो सूत्रों का उपयोग करके हल करना मुश्किल या असंभव है।


























