
गणित की पहेलियाँ अकल्पनीय हैंकी राशि। उनमें से प्रत्येक अपने तरीके से अद्वितीय है, लेकिन उनका आकर्षण इस तथ्य में निहित है कि इसे हल करने के लिए अनिवार्य रूप से सूत्र में आना चाहिए। बेशक, आप उन्हें हल करने की कोशिश कर सकते हैं, जैसा कि वे कहते हैं, यादृच्छिक पर, लेकिन यह बहुत लंबा और लगभग असफल होगा।
इस लेख में से एक के बारे में बात करेंगेइस तरह के रहस्य, और अधिक सटीक होने के लिए - जादू वर्ग के बारे में। हम विस्तार से विश्लेषण करेंगे कि जादू वर्ग को कैसे हल किया जाए। सामान्य शिक्षा कार्यक्रम के ग्रेड 3, बेशक, यह गुजरता है, लेकिन शायद सभी को समझ नहीं आया या बिल्कुल याद नहीं है।
जादू वर्ग, या, जैसा कि इसे कहा जाता है,जादुई एक तालिका है जिसमें कॉलम और पंक्तियों की संख्या समान होती है, और वे सभी अलग-अलग संख्याओं से भरे होते हैं। मुख्य कार्य यह है कि ऊर्ध्वाधर, क्षैतिज और विकर्ण की मात्रा में ये आंकड़े समान मूल्य देते हैं।
जादू वर्ग के अलावा, वहाँ भी हैsemimagic। तात्पर्य यह है कि संख्याओं का योग केवल लंबवत और क्षैतिज रूप से समान होता है। जादू वर्ग "सामान्य" केवल तभी होता है जब एक से प्राकृतिक संख्याओं को भरने के लिए उपयोग किया जाता है।
एक सममित जादू वर्ग के रूप में अभी भी ऐसी चीज है - यह तब है जब दो अंकों के योग का मूल्य बराबर होता है, जबकि उन्हें केंद्र के संबंध में सममित रूप से व्यवस्थित किया जाता है।
यह जानना भी महत्वपूर्ण है कि वर्ग 2 से 2 के अलावा किसी भी आकार के हो सकते हैं। 1 बाय 1 का एक वर्ग भी जादू माना जाता है, क्योंकि सभी शर्तें पूरी होती हैं, हालांकि इसमें एक ही संख्या होती है।
तो, हमने जो परिभाषा पढ़ी है, उसके साथ अब बात करते हैं कि जादू वर्ग को कैसे हल किया जाए। स्कूल पाठ्यक्रम के ग्रेड 3 में इस लेख के बारे में विस्तार से सब कुछ समझाने की संभावना नहीं है।
वे लोग जो जादुई को हल करना जानते हैंएक वर्ग (कक्षा 3 निश्चित रूप से जानता है), वे तुरंत कहते हैं कि केवल तीन समाधान हैं, और उनमें से प्रत्येक अलग-अलग वर्गों के लिए उपयुक्त है, लेकिन फिर भी, चौथे समाधान की उपेक्षा करना असंभव है, जिसका नाम "यादृच्छिक पर" है। वास्तव में, कुछ हद तक यह संभावना है कि एक अनजान व्यक्ति अभी भी इस पहेली को हल करने में सक्षम होगा। लेकिन हम इस पद्धति को एक लंबे बॉक्स में छोड़ देंगे और सीधे सूत्रों और विधियों के लिए आगे बढ़ेंगे।
यह विधि केवल ऐसे वर्ग को हल करने के लिए उपयुक्त है, जिसमें कोशिकाओं की संख्या विषम है, उदाहरण के लिए, 3 बाय 3 या 5 बाय 5।
तो, किसी भी मामले में, शुरू में जादू को खोजने के लिए आवश्यक है। यह वह संख्या है जो तिरछे, लंबवत और क्षैतिज रूप से संख्याओं के योग के साथ प्राप्त की जाएगी। यह सूत्र का उपयोग करके गणना की जाती है:
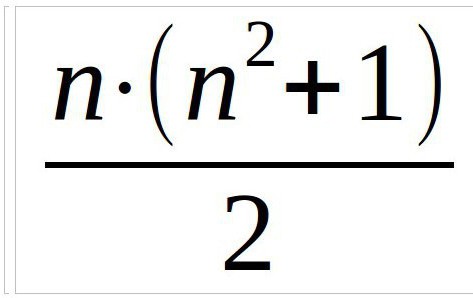
इस उदाहरण में, हम एक तीन बाय तीन वर्ग पर विचार करेंगे, इसलिए सूत्र इस तरह दिखेगा (n कॉलम की संख्या है):
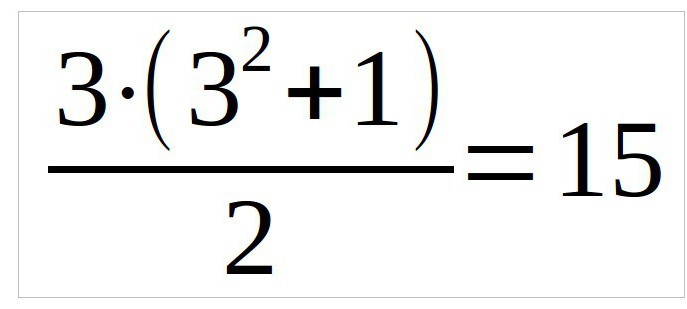
तो, हमारे पास एक वर्ग है। पहली बात यह है कि शीर्ष पर पहली पंक्ति के केंद्र में नंबर एक दर्ज करना है। बाद के सभी नंबरों को सही विकर्ण पर एक स्थान रखा जाना चाहिए।
लेकिन फिर सवाल तुरंत उठता है कि जादू को कैसे हल किया जाएवर्ग? ग्रेड 3 इस पद्धति का उपयोग करने की संभावना नहीं है, और बहुमत में एक समस्या होगी, अगर इस तरह की सेल नहीं है तो इस तरह से कैसे करें? सब कुछ सही करने के लिए, आपको कल्पना को चालू करने और शीर्ष पर एक समान जादू वर्ग खींचने की आवश्यकता है और यह पता चलता है कि नंबर 2 निचले दाएं सेल में होगा। इसलिए, हमारे वर्ग में, हम एक ही स्थान पर एक दो में प्रवेश करते हैं। इसका मतलब है कि हमें संख्याओं को दर्ज करने की आवश्यकता है ताकि कुल में वे 15 का मान दें।
इसके बाद की संख्याएं बिल्कुल एक जैसी हैं।यानी, 3 पहले कॉलम के केंद्र में होंगे। लेकिन इस सिद्धांत पर 4 प्रवेश नहीं कर पाएंगे, क्योंकि इसकी जगह पहले से ही एक इकाई है। इस स्थिति में, संख्या 4 को 3 के नीचे रखा गया है, और जारी रखें। पांच - वर्ग के केंद्र में, 6 - ऊपरी दाएं कोने में, 7 - 6 के नीचे, 8 - ऊपरी बाएं में और 9 नीचे तल के केंद्र में।
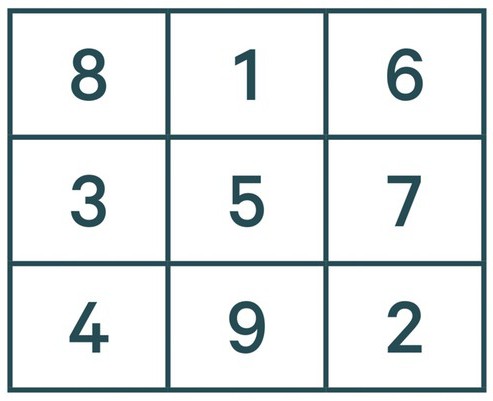
अब आप जानते हैं कि जादू वर्ग को कैसे हल किया जाए।ग्रेड 3 डेमिडोव पारित हो गया, लेकिन इस लेखक के पास थोड़ा सरल काम था, हालांकि, इस पद्धति को जानते हुए, इस तरह की समस्या को हल करना संभव होगा। लेकिन अगर स्तंभों की संख्या विषम है। और क्या करें यदि, उदाहरण के लिए, हमारे पास 4 बाय 4 वर्ग है? पाठ में इसके बारे में आगे।
डबल समता का वर्ग वह है जिसमें स्तंभों की संख्या को 2 में विभाजित किया जा सकता है और 4. अब हम एक वर्ग 4 को 4 से मानते हैं।
तो, मैजिक स्क्वायर (ग्रेड 3, डेमिडोव, कोज़लोव, टोंकिख - एक गणित पाठ्यपुस्तक में एक कार्य) को कैसे हल किया जाए, जब इसके स्तंभों की संख्या 4 है? एक बहुत ही सरल। पहले के उदाहरण की तुलना में आसान है।
पहले हम जादू को स्थिर पाते हैंवही सूत्र जो पिछली बार उद्धृत किया गया था। इस उदाहरण में, संख्या 34 है। अब आपको संख्याओं को बनाने की आवश्यकता है ताकि ऊर्ध्वाधर, क्षैतिज और विकर्ण का योग समान हो।
सबसे पहले आपको कुछ कोशिकाओं को पेंट करने की आवश्यकता है,आप इसे एक पेंसिल के साथ या कल्पना में कर सकते हैं। हम सभी कोनों पर पेंट करते हैं, यानी ऊपरी बाएँ सेल और ऊपरी दाएँ, निचले बाएँ और निचले दाएँ। यदि वर्ग 8 से 8 था, तो कोने में एक सेल पर नहीं, बल्कि चार, 2 से 2 आकार में पेंट करना आवश्यक है।
अब इस वर्ग के केंद्र पर पेंट करना आवश्यक है, ताकि इसके कोने पहले से चित्रित कोशिकाओं के कोनों को छू सकें। इस उदाहरण में, हमें 2 से 2 के केंद्र में एक वर्ग मिलता है।
शुरुआत हो रही है।हम बाएं से दाएं को भरेंगे, जिस क्रम में कोशिकाएं स्थित हैं, केवल हम भरे हुए कक्षों में मान दर्ज करेंगे। यह पता चला है कि ऊपरी बाएँ कोने में हम 1 में प्रवेश करते हैं, दाईं ओर - 4. फिर हम केंद्रीय 6, 7 और आगे 10, 11. में भरते हैं निचले बाएँ 13 और दाएं - 16। हमें लगता है कि भरने का क्रम स्पष्ट है।

शेष कोशिकाओं को उसी तरह से भरा जाता है, केवल अंदरअवरोही क्रम। यही है, चूंकि अंतिम अंकित आंकड़ा 16 था, इसलिए हम वर्ग के शीर्ष पर 15 लिखते हैं। फिर 14. फिर 12, 9 और इसी तरह, जैसा कि चित्र में दिखाया गया है।
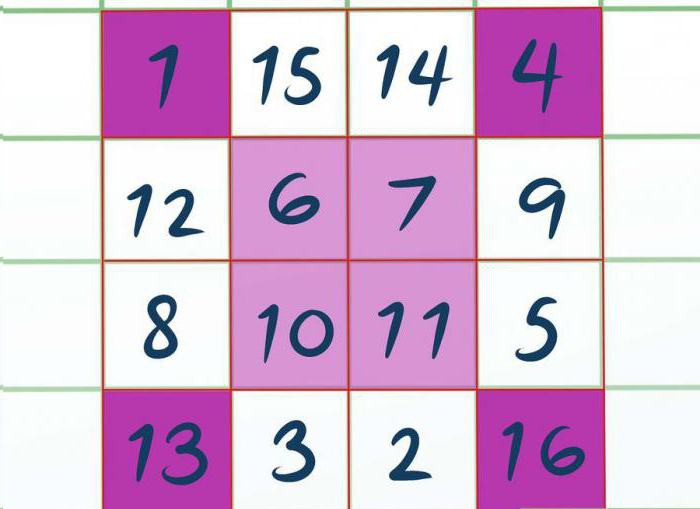
अब आप जादू वर्ग को हल करने का दूसरा तरीका जानते हैं। ग्रेड 3 इस बात से सहमत है कि दूसरों की तुलना में डबल-पैरिटी वर्ग को हल करना बहुत आसान है। खैर, हम अंतिम विधि पर जाते हैं।
एकल समता का एक वर्ग कहा जाता है, उस वर्ग को, जिसके स्तंभों की संख्या को दो में विभाजित किया जा सकता है, लेकिन चार नहीं। इस मामले में, यह 6 बाय 6 वर्ग है।
तो, हम जादू की निरंतर गणना करते हैं। वह 111 के बराबर है।
अब हमें अपने वर्ग को नेत्रहीन रूप से विभाजित करने की आवश्यकता है3 बाय 3 के चार अलग-अलग वर्ग। चार बड़े वर्ग होते हैं, जिनमें 3 में 3 बड़े होते हैं, जिनमें से 6 में 6 होते हैं। ऊपरी बाएँ को A कहा जाता है, निचले दाएं को B, ऊपरी दाएं को C और निचले को बाएं को D कहा जाता है।

अब हर छोटे वर्ग की जरूरत हैइस लेख में दिए गए पहले तरीके का उपयोग करके हल करें। यह पता चला है कि वर्ग ए में 1 से 9 तक, बी में - 10 से 18 तक, सी में - 19 से 27 और डी - 28 से 36 तक संख्या होगी।
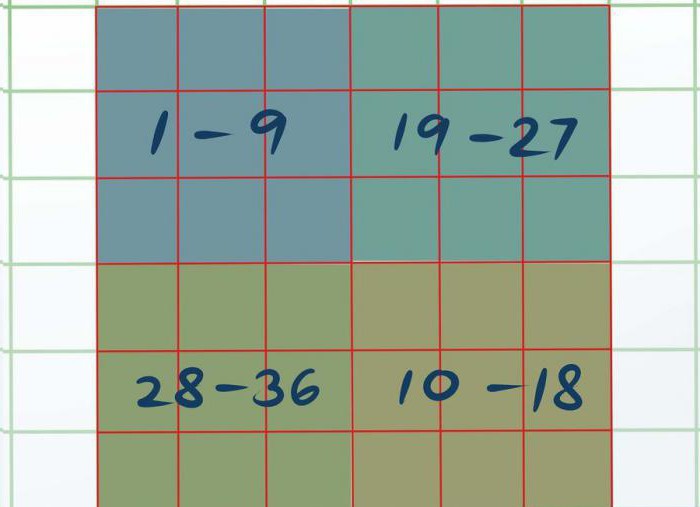
एक बार जब आप सभी चार वर्गों को हल कर लेते हैं, तो काम करेंA और D पर शुरू होगा। वर्ग A में तीन कोशिकाओं का चयन करना आवश्यक है, एक नेत्रहीन या एक पेंसिल के साथ, अर्थात्: ऊपरी बाएँ, मध्य और निचले बाएँ यह पता चला है कि हाइलाइट किए गए नंबर 8, 5 और 4 हैं। उसी तरह, वर्ग डी (35, 33, 31) को हाइलाइट किया जाना चाहिए। सभी शेष राशि वर्ग डी से ए तक आवंटित अंकों को स्वैप करना है।
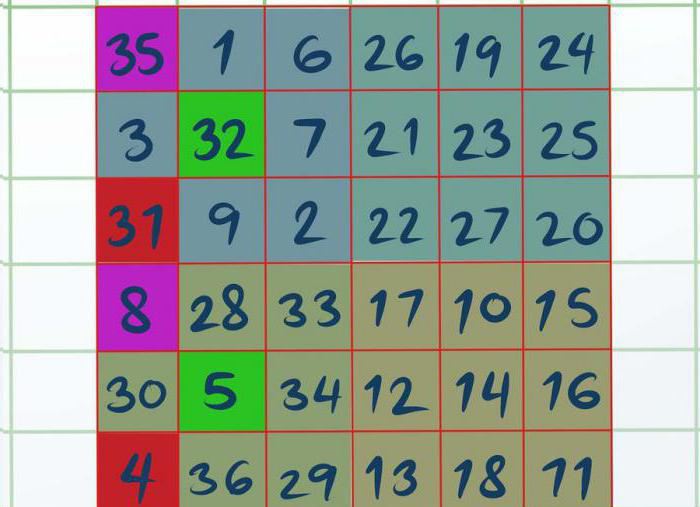
अब आप जादू वर्ग को हल करने का अंतिम तरीका जानते हैं। 3 वर्ग वर्ग एकल समता सबसे अधिक पसंद नहीं है। और यह आश्चर्य की बात नहीं है, उन सभी में से यह सबसे जटिल है।
इस लेख को पढ़ने के बाद, आपने सीखा कि कैसे हल किया जाएजादू वर्ग। ग्रेड 3 (मोरो - पाठ्यपुस्तक के लेखक) केवल कुछ भरी हुई कोशिकाओं के साथ समान कार्य प्रदान करता है। उसके उदाहरणों पर विचार करने का कोई मतलब नहीं है, क्योंकि सभी तीन तरीकों को जानने के बाद, आप आसानी से सभी प्रस्तावित समस्याओं को हल कर सकते हैं।


























