
Trokut je jedan od najčešćihgeometrijskim oblicima, s kojima smo upoznati u osnovnoj školi. Pitanje kako pronaći područje trokuta, svaki se student suočava u satovima geometrije. Dakle, koja su obilježja pronalaženja područja ove brojke mogu se identificirati? U ovom članku ćemo pogledati osnovne formule potrebne za obavljanje takvog zadatka, kao i analizirati vrste trokuta.

Područje trokuta možete pronaći na potpuno različite načine, jer u geometriji postoji više od jednog oblika oblika koji sadrži tri ugla. Te vrste uključuju:
Razmotrimo detaljnije svaku od postojećih tipova trokuta.

Takav se geometrijski oblik smatra najvećimuobičajeni u rješavanju geometrijskih problema. Kada se pojavi potreba za crtanjem proizvoljnog trokuta, spašava se ta opcija.
U akutnom trokutu, kao što naziv implicira, svi su kutovi oštri i dostižu 180 °.
Ovaj je trokut također vrlo čest,međutim, nalazi se nešto rjeđe oštroumno. Na primjer, pri rješavanju trokuta (to jest, znate nekoliko njegovih strana i kutova i trebate pronaći preostale elemente), ponekad morate utvrditi je li kut obupan ili ne. Kosinus nejasnog kuta je negativan broj.
U tupom trokutu jedan je kut veći od 90 °, tako da preostala dva kuta mogu uzeti male vrijednosti (na primjer, 15 ° ili čak 3 °).
Da biste pronašli područje trokuta ove vrste, morate znati neke nijanse, o kojima ćemo govoriti dalje.
Uobičajeni poligon je likuključujući n uglove u kojima su sve strane i kutovi jednaki. Ovo je redoviti trokut. Budući da je zbroj svih kutova trokuta 180 °, svaki od tri kuta je 60 °.
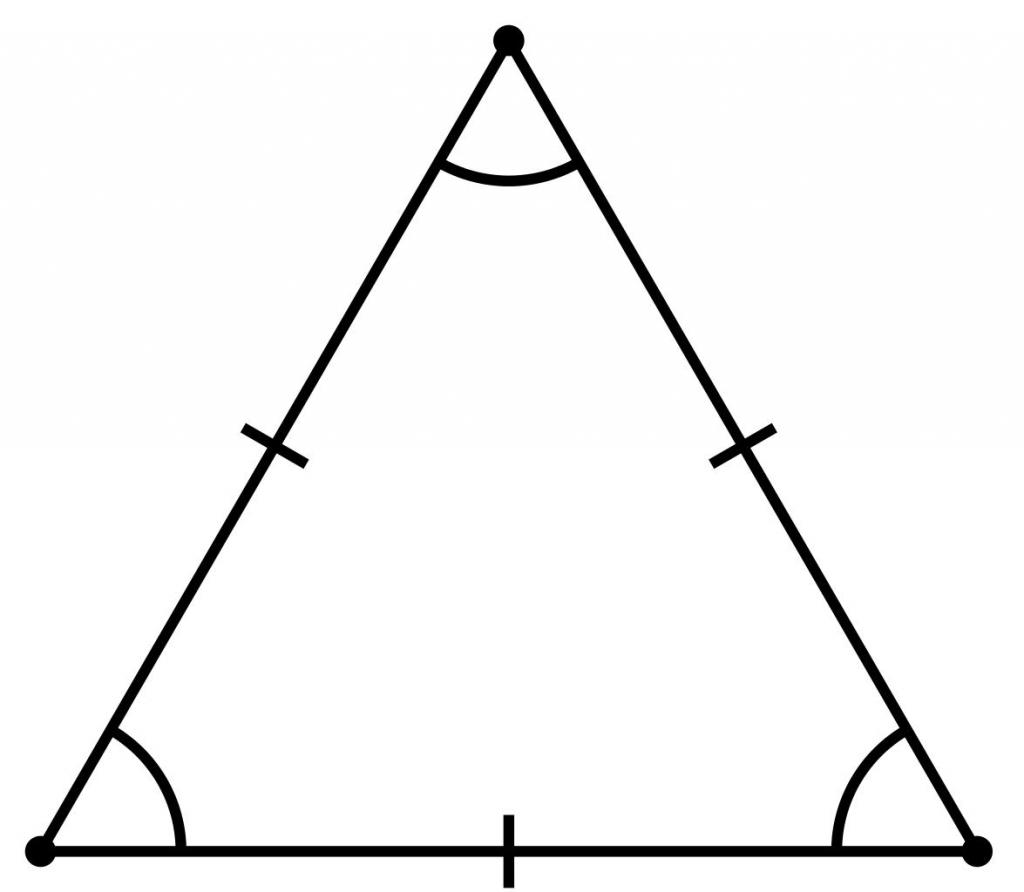
Pravi trokut, zbog svog svojstva, naziva se i jednakostraničan lik.
Također je vrijedno napomenuti da se samo jedan krug može upisati u pravilan trokut, a oko njega se može opisati samo jedan krug, a njihovi centri su smješteni u jednoj točki.

Помимо равностороннего типа, можно также выделить isosceles trokut, malo različit od njega. U takvom su trokutu dvije strane i dva kuta jednaki jedna drugoj, a treća strana (kojoj su jednaki kutovi susjedni) je osnova.
Na slici je prikazan jednako jednaki trokut DEF, čiji su kutovi D i F jednaki, a DF baza.

Pravokutni trokut je tako nazvan jer je jedan od njegovih uglova ravno, to jest, jednak je 90 °. Druga dva kuta daju se i do 90 °.
Najveća strana takvog trokuta, koja leži nasuprot kutu od 90 °, je hipotenuza, dok su ostale dvije njegove strane noge. Za ovu vrstu trokuta primjenjiva se pitagorejska teorema:
Zbir kvadrata duljina nogu jednak je kvadraturi duljine hipotenuze.
Na slici je prikazan trokut pod pravim kutom BAC s hipotenuzom AC i nogama AB i BC.
Da biste pronašli područje trokuta s pravim kutom, morate znati numeričke vrijednosti njegovih nogu.
Prijeđimo na formule za pronalaženje područja ove figure.
U geometriji se mogu razlikovati dvije formule kojepogodni su za pronalaženje područja većine vrsta trokuta, naime za trokute s oštrim, kutnim i redovitim isoscelama. Analizirajmo svaki od njih.
Ova je formula univerzalna zapronalazeći područje figure koju razmatramo. Da biste to učinili, dovoljno je znati duljinu bočne strane i duljinu visine povučene na nju. Sama formula (polovica proizvoda baze i visine) je sljedeća:
S = ½ * A * H,
gdje je A strana zadanog trokuta, a H visina trokuta.

Na primjer, da biste pronašli područje trokuta oštrog kuta ACB, pomnožite njegovu stranu AB s CD-om visine i podijelite dobivenu vrijednost s dva.
Međutim, nije uvijek lako pronaći to područjetrokut na ovaj način. Na primjer, da biste ovu formulu koristili za nejasan trokut, trebate nastaviti jednu od njegovih strana i tek nakon toga nacrtati visinu na nju.
U praksi se ta formula koristi češće od ostalih.
Ova formula, kao i prethodna, prikladna jevećine trokuta i u njegovom značenju posljedica je formule za pronalaženje područja pokraj i visine trokuta. Odnosno, razmatrana formula se lako može izvesti iz prethodne. Njegova formulacija izgleda ovako:
S = ½ * sinO * A * B,
gdje su A i B stranice trokuta, a O je kut između strana A i B.
Podsjetimo da se sinus kutova može vidjeti u posebnoj tablici nazvanoj po izvrsnom sovjetskom matematičaru V. M. Bradisu.
A sada prijeđimo na ostale formule koje su prikladne samo za iznimne vrste trokuta.
Uz univerzalnu formulu, koja uključuje potrebu za crtanje visine u trokutu, noge trokuta koji sadrže pravi kut mogu se naći i pod njegovim nogama.
Dakle, područje trokuta koji sadrži pravi kut je polovina proizvoda njegovih nogu, ili:
S = ½ * a * b,
gdje su a i b noge pravokutnog trokuta.
Ova vrsta geometrijskih oblika razlikuje se u tomeda se njegovo područje može naći za naznačenu vrijednost samo jedne njegove strane (jer su sve strane pravilnog trokuta jednake). Dakle, suočeni s problemom "pronađite područje trokuta kad su strane jednake", trebate koristiti sljedeću formulu:
S = A2* √3 / 4,
gdje je A strana jednakostraničnog trokuta.
Posljednja opcija za pronalaženje područja trokuta je Heronova formula. Da biste ga koristili, morate znati duljine triju strana figure. Heronova formula izgleda ovako:
S = √p (p - a) (p - b) (p - c),
gdje su a, b i c strane ovog trokuta.
Ponekad je problem problem:"Područje pravilnog trokuta - pronađite duljinu njegove stranice". U ovom slučaju trebate koristiti formulu koja nam je već poznata za pronalaženje područja pravilnog trokuta i iz njega dobivate vrijednost strane (ili njegovog kvadrata):
A2 = 4S / √3.
U problemima GIA-e u matematici postoji mnogo formula. Osim toga, često je potrebno na kariranom papiru pronaći područje trokuta.
U ovom je slučaju najprikladnije nacrtati visinu na jednu od strana slike, odrediti njezinu duljinu po ćelijama i pomoću univerzalne formule pronaći područje:
S = ½ * A * H.
Dakle, nakon proučavanja formula prikazanih u članku, nećete imati problema s pronalaženjem područja trokuta bilo koje vrste.


























