
Trikampis yra viena iš pagrindinių planimetrijos figūrų.Būtent su juo pagal mokyklos programą pradedamas tikrosios, tam tikra prasme, geometrijos tyrimas. Atsižvelgiant į kampų tipą, šio tipo figūras galima suskirstyti į keletą tipų. Sprendžiant problemas, lengviausias paprastai laikomas stačiakampiu. Jam yra daugybė teoremų, taisyklių, taip pat trigonometrinių funkcijų, leidžiančių rasti bet kurią koją ar hipotenuzę, žinant tik vienos iš šonų ilgį ir kampą (bet kurį, išskyrus tiesią).
Tačiau jei egzistuotų tik tokia rūšistrikampiai, aukštųjų ir vidurinių mokyklų moksleivių gyvenimas būtų daug paprastesnis ir nerūpestingas. Bet taip nėra. Kiekviena figūra, kurią tiria geometrija, turi savo ypatybes ir savybes. Norėdami užtikrintai išspręsti problemas, turite žinoti visų daugiakampių savybes.

Lygiašonis trikampis yra labai panašus į augintinįPitagoras, kuris buvo paminėtas įvade. Taisykles, susijusias su jo konstrukcija ar nežinomų elementų radimu, supras net penktasis greideris. Svarbiausia gerai žinoti pagrindines geometrijos sąvokas ir pagrindinius plokščių figūrų elementus.
Свойства равнобедренного треугольника выплывают nuo jo struktūros. Du kampai ties tokio daugiakampio pagrindu yra tokie patys kaip ir šonai. Iškart iš šios informacijos galime padaryti neabejotiną išvadą. Norint rasti smailės laipsnio matą, žinant vieną iš pagrindo kampų, reikia padauginti jį iš dviejų ir atimti iš 180 °. Dvi pusės, kurių kraštiniai taškai yra viršuje ir apačioje, vadinamos šoninėmis.
Taisyklių, kurių šis skaičius neturi, viskas išdėstytaužduotys kyla iš jo konstrukcijos, todėl jos suprantamos ir patogios studentams. Tačiau yra viena pagrindinė savybė, kurią galima vadinti lygiašonio trikampio vidurio savybe. Viskas dėl jos dvigubos prigimties. Jei ant popieriaus reikia pastatyti tokį trikampį pagal visas taisykles, tada galite pamatyti, kad linija centre yra ne tik vidurinė, bet ir aukštis bei bisektorius.
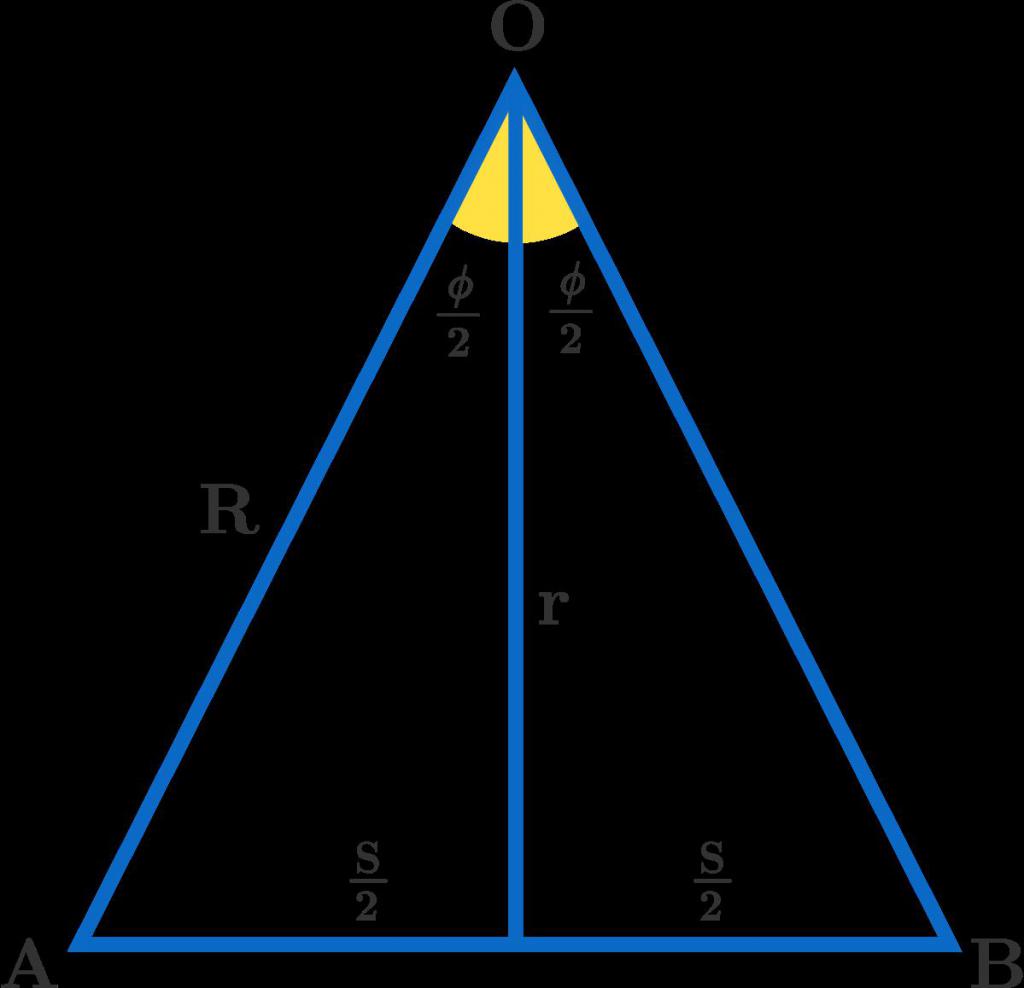
Linija, brėžta iš viršaus į apačią,nebus toks vienareikšmis. Jo savybes lemia pagrindiniai lygiašonio trikampio bruožai. Nukritęs nuo viršūnės kampo į pagrindą, jis sukuria du lygius trikampius, o su pagrindu sudaro statmeną, padalijančią ją į lygius segmentus. Tokio tipo trikampių nereikėtų painioti su lygiakraščiais trikampiais (dažnai tokią klaidą daro studentai). Jie turi tris vienodus kampus, o ne du, kaip čia.


























