
Ability to correctly display different shapes on a plane sheet, canvas and any other surface issufficiently significant skill. And first of all it is important for people of art: painters, sculptors, graphic artists, designers (interior spaces of buildings and architectural environment), and for people of science: mathematicians, physicists, designers, inventors.
But also to the person far from these spheres, to learncorrectly perceive and reflect the surrounding world is also important. This helps to understand much more of its versatility. If there is not enough understanding of how to do it correctly, then the project, picture or drawing of any invention is unlikely to succeed. That is, this skill is important both for solving simple, everyday tasks, and for having a global, universal significance.
Since ancient times, people have tried to portray,that they saw around themselves: other people, some primitive structures of those times, a surprisingly beautiful world of plants and animals, majestic mountains, and just things, household items. That is, peace in all its diversity and grandeur.
But then they did not yet have an idea of how thisit is possible to implement accurately and correctly, so that the display of different volumetric objects on the plane is really realistic, alive. There was no adequate knowledge for a person, and especially lack of special skills, apart from, perhaps, the most elementary.
It is said in earlier sources thatthe first picture in the world consisted of only one line, which ran along the shadow of a man thrown back by the sun against a wall. That is, nature itself prompted in which direction it is necessary to move in search of the correct solution of this issue.
And this question excited the person of that time stilland that's why: he did not want to just admire the voluminous living silhouette, the original, so to speak, but sought to capture a spatial object on the plane. And he did this so that it would be possible in this way to either decorate his home or place sacred to him, or take a package with a drawing and carry it to any distance.
And whatever you say, but the years went by, centuries passedand somehow as civilization developed, people gradually learned to display complex figures in two-dimensional space, that is, on a plane. Only here the accuracy of the sizes and proportions of the depicted objects began to seem very approximate.
But the question of how correctly the mappingfigures on the plane and how much they correspond to the voluminous original objects, has become one day very relevant. In a way, a new science, called geometry, has helped in solving this issue. Or rather, its section is descriptive geometry.
Here she is just studying shapes and planes, straight lines and points, and also their relationship to each other - both in three-dimensional and two-dimensional space.
An important feature in the visual artsis the display of shapes in the image plane. After all, in fact, this is the imprint of three-dimensional spatial objects in two-dimensionality. Namely: the complex must be converted into a simple, that is, an object that has a length, width, height, you need to translate into a plane.
And descriptive geometry performs such "transitions", thanks to some methods. In all there are about six. Here are the three main ones and the most popular in the whole world:
Достаточно наглядно предстает изображаемый объект in the axonometric projection (to which the orthogonal and oblique angles are referred). But most clearly and truly he is projected when portrayed in perspective. And it is the above mentioned methods that largely solve the problem of how to make the mapping of figures on a plane.

Perspective among other ways of imageoccupies the most honorable place. Because the human eye, like the camera lens, sees the surrounding space in a similar way. Things that are farther from the observer, in size, look smaller, and sometimes much less than when they are near.
For example, take the image of a cube in space.If, in fact, all its edges are parallel to each other, then when you look at this object in the distance, it may seem that the edges converge (or should converge) at one point. And, most interestingly, it is not just necessary to converge at one point, but have a single point of intersection.
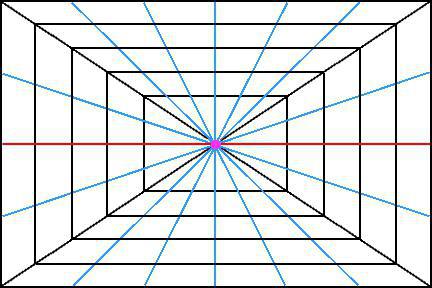
Thanks to the masters of the Renaissance:Albrecht Durer, Piero Della Francesca, Andrea Mantegna, Leon Batista Alberti, contemporary painting knows what a direct linear perspective is, how to determine the height of the horizon and the points of descent.
A world-famous genius - Leonardo da Vinci -for the first time argued the concept of aerial perspective. This is a change in color, the tone of the object, changes in its contrast characteristics (decrease as the object is removed).

Orthogonal is called paralleldesign that is directed to a line that is perpendicular to the plane. In the process of its application, the dimensions of the contours of the object remain unchanged. That is, the object is displayed without distortion.
Projected three-dimensional objectdecomposed into three types: side, front and top. And looking at all this at the same time, you can add up the idea of how the object looks in volume. At the same time, the size of the figure remains unchanged both in the three-dimensional image and in the two-dimensional one.

This projection is further subdivided into several subspecies, namely:
Do isometric distortion factors in all3 axes (in length, width, height). That is, the angles between the axles taken in pairs are 120 degrees. In dimetric - the distortions along the 2nd axes are equal, and the third is different. And in the trimetric projection, all the distortion coefficients (that is, along all 3 axes) are different.
When rotating a right triangle along the axisone of the two legs of his third party (hypotenuse) will describe a new figure called a cone. And if you rotate the rectangle (square) on one of its sides, you get a cylinder. If you rotate the semicircle, a sphere will come out.
It follows that by rotating the plane along some axis, we get the so-called figures of rotation.

These figures have an axis of rotation.How they look in a plane depends on their placement relative to eye level. For example, the upper and lower sides of a cylinder are essentially circles. And if you look at them in a plane, they look like ellipses.
But the task becomes even more difficult ifdisplaying spatial figures on a plane, they have an inclined axis. It is important that the contours of the bodies of rotation were equidistant from the axis of the latter.
Важную роль при отображении фигур на плоскости chiaroscuro plays. Because the volume of the imaged object is created not only due to the lines, but also due to the correct distribution of light and shadow on its sides. And then it looks quite voluminous in the plane of a two-dimensional surface.

Thus, the display of the figures on the plane,Determination of their sizes, features of proper blending of lightness and dark spots are quite possible due to the methods listed above. And, most importantly, these are already truly proven methods that are used by leading experts of our time.


























