Basic MKT equation and temperature measurement

The study of processes occurring in statisticalsystems, is complicated by the minimum size of particles and a huge number of them. It is practically impossible to consider each particle separately, therefore statistical values ​​are introduced: the mean velocity of the particles, their concentration, the mass of the particle. The formula characterizing the state of the system with allowance for microscopic parameters is called the basic equation of the molecular-kinetic theory of gases (MKT).

A little about the average speed of the particles

The determination of the velocity of motion of particles was firstwas carried out experimentally. Known from the school program experience, conducted by Otto Stern, allowed to create an idea of ​​the velocities of particles. In the course of the experiment, the motion of silver atoms in rotating cylinders was investigated: first, in a stationary state of the installation, then when it rotated at a certain angular velocity.

As a result, it was found that the velocity of the moleculessilver exceeds the speed of sound and is 500 m / s. The fact is quite interesting, because it is difficult to sense such velocities of particle motion in substances.

Perfect gas

Continue research is possibleOnly in a system whose parameters can be determined by direct measurements using physical instruments. Speed ​​is measured with a speedometer, but the idea of ​​attaching a speedometer to an individual particle is absurd. One can directly measure only the macroscopic parameter associated with the motion of particles.

Let us consider the gas pressure.The pressure on the walls of the vessel is created by blowing the molecules of the gas in the vessel. The peculiarity of the gaseous state of matter is in sufficiently large distances between the particles and their small interaction with each other. This allows you to directly measure its pressure.

Any system of interacting bodiescharacterized by the potential energy and kinetic energy of motion. Real gas is a complex system. Variability of potential energy can not be systematized. The problem can be solved by introducing a model carrying the characteristic properties of the gas, which sweeps out the complexity of the interaction.

Ideal gas is a state of matter in whichthe interaction of the particles is negligible, the potential energy of the interaction tends to zero. Considerable only the energy of motion, which depends on the velocity of the particles, can be considered important.

The ideal gas pressure

Identify the relationship between gas pressure and velocitythe motion of its particles allows the basic equation of the MKT of an ideal gas. A particle moving in a vessel, when colliding with a wall, transmits to it a pulse, the magnitude of which can be determined on the basis of Newton's second law:

• FΔt = 2m₀at_from

The change in the momentum of a particle in an elastic impact is associated with a change in the horizontal component of its velocity. F is the force acting on the side of the particle on the wall for a short time t; m₀ Is the mass of the particle.

With a surface area S, for a time Δt all gas particles moving in the direction of the surface with velocity v collide_from and located in a cylinder of volume Sv_fromΔt. At a particle concentration n exactly half of the molecules move to the wall, the second half - in the opposite direction.

After considering the collision of all particles, we can write Newton's law for the force acting on the pad:

• FΔt = nm₀at_from²SΔt

Since the gas pressure is defined as the ratio of the force acting perpendicular to the surface to the area of ​​the latter, we can write:

• p = F: S = nm₀at_from²

The resulting relation as the basic MKT equation can not describe the whole system, since only motion in one direction is considered.

Maxwell distribution

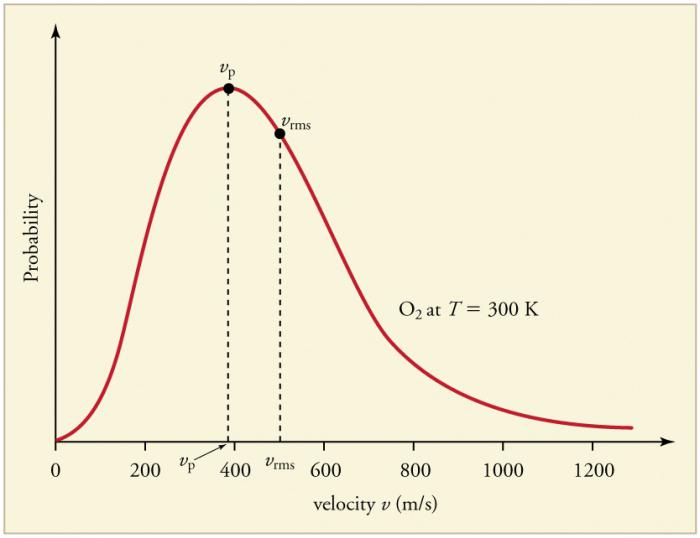
Continuous frequent collisions of gas particles withwalls and with each other lead to the establishment of a certain statistical distribution of particles in terms of velocities (energies). The directions of all the velocity vectors turn out to be equally probable. This distribution was called the Maxwell distribution. In 1860, this pattern was deduced by Maxwell on the basis of the MKT. The main parameters of the distribution law are velocities: probable, corresponding to the maximum value of the curve, and the rms v_square = √ 2›Is the mean of the square of the particle velocity.

An increase in the gas temperature corresponds to an increase in the value of the velocities.

Proceeding from the fact that all speeds are equal, and their modules have the same value, we can assume:

• 2> = from²> + and²> + z²>, From which: from²> = 2>: 3

The basic MKT equation taking into account the average value of the gas pressure is:

• p = nm₀2>: 3.

This relationship is unique in that it determines the relationship between microscopic parameters: velocity, particle mass, particle concentration and gas pressure as a whole.

Using the concept of kinetic energy of particles, the basic MKT equation can be rewritten in a different way:

• p = 2nm₀2>: 6 = 2n to>: 3

The gas pressure is proportional to the average value of the kinetic energy of its particles.

Temperature

It is interesting that for an unchanged amount of gas inA closed vessel can be associated with the gas pressure and the average energy of the particle motion. The measurement of the pressure can be made by measuring the energy of the particles.

How to proceed? What value can be compared with the kinetic energy? Such a value is the temperature.

Temperature is a measure of the thermal state of substances.To measure it, a thermometer is used, based on the thermal expansion of the working fluid (alcohol, mercury) with heating. The scale of the thermometer is created experimentally. Usually marks are placed on it, corresponding to the position of the working body with a certain physical process, taking place with a constant thermal state (boiling water, melting ice). Different thermometers have different scales. For example, the scale Celsius, Fahrenheit.

Universal temperature scale

More interesting from the point of view of independence fromthe properties of the working fluid can be considered gas thermometers. Their scale does not depend on the kind of gas used. In such an instrument, we can hypothetically identify the temperature at which the gas pressure tends to zero. Calculations show that this value corresponds to -273.15 ^aboutWITH.The temperature scale (absolute temperature scale or Kelvin scale) was introduced in 1848. For the main point of this scale took the possible temperature of zero gas pressure. A single segment of the scale is equal to a single value of the Celsius scale. It is more convenient to write the basic MKT equation using temperature when studying gas processes.

The relationship of pressure and temperature

Experimentally, you can verify the proportionality of the gas pressure to its temperature. At the same time, it was found that the pressure is directly proportional to the concentration of particles:

• P = nkT

where T is the absolute temperature, k is a constant value equal to 1.38 • 10^-23J / C.

The fundamental value having a constant value for all gases is called the Boltzmann constant.

Comparing the dependence of pressure on temperature and the basic equation of the MKT of gases, we can write:

• ‹E_to›= 3kT: 2

The average value of the kinetic energy of the movement of gas molecules is proportional to its temperature. That is, the temperature can serve as a measure of the kinetic energy of particle motion.