
In space, the plane can be set differentways (one point and vector, two points and vector, three points, etc.). With this in mind, the equation of the plane can have various forms. Also, if certain conditions are met, planes can be parallel, perpendicular, intersecting, etc. About this and talk in this article. We will learn to make up the general equation of the plane and not only.
Suppose there is a space R3, which has a rectangular coordinate system XYZ. Let us define the vector α, which will be released from the initial point O. Through the end of the vector α we draw the plane P, which will be perpendicular to it.
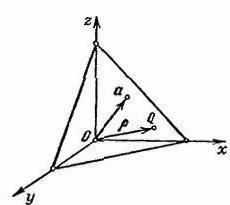
Denote on произвольн an arbitrary point Q = (x, y, z). The radius vector of the point Q will be signed with the letter p. The length of the vector α is equal to p = IαI and Ʋ = (cosα, cosβ, cosγ).
This is the unit vector that is directed toside, like vector α. α, β and γ are the angles that are formed between the vector Ʋ and the positive directions of the axes of the x, y, z space, respectively. The projection of any point QϵP on the vector Ʋ is a constant, which is equal to p: (p, Ʋ) = p (p ≥0).
The indicated equation makes sense when p = 0.The only plane P in this case will intersect the point O (α = 0), which is the origin, and the unit vector, released from the point O, will be perpendicular to P, despite its direction, which means that the vector is defined with accuracy to the mark. The previous equation is an equation of our plane P, expressed in vector form. But in the coordinates of his view will be:

P here is greater than or equal to 0. We found the equation of a plane in space in a normal form.
If the equation in coordinates is multiplied by any number that is not equal to zero, we obtain an equation equivalent to this one, which determines that same plane. It will look like this:

Here A, B, C are numbers that are nonzero at the same time. This equation is referred to as a general plane equation.
The equation in general form can be modified if there are additional conditions. Consider some of them.
Suppose that the coefficient A is equal to 0. This means that this plane is parallel to the given axis Ox. In this case, the form of the equation will change: Wu + Cz + D = 0.
Similarly, the form of the equation will change under the following conditions:
In the case when the numbers A, B, C, D are non-zero, the type of equation (0) may be as follows:
x / a + y / b + z / c = 1,
in which a = -D / A, b = -D / B, c = -D / C.
As a result, we obtain the equation of the plane in the segments. It should be noted that this plane will cross the Ox axis at the point with coordinates (a, 0,0), Oy - (0, b, 0), and Oz - (0,0, s).

Taking into account the equation x / a + y / b + z / s = 1, it is easy to visualize the placement of the plane relative to a given coordinate system.
The normal vector n to the plane P has coordinates, which are coefficients of the general equation of the given plane, that is, n (A, B, C).

To determine the coordinates of the normal n, it suffices to know the general equation of a given plane.
When using the interval equation, whichhas the form x / a + y / b + z / c = 1, as with the use of the general equation, you can write the coordinates of any normal vector of a given plane: (1 / a + 1 / b + 1 / s)
Стоит отметить, что нормальный вектор помогает solve a variety of tasks. The most common are problems that consist in proving the perpendicularity or parallelism of planes, the problem of finding the angles between planes or the angles between planes and lines.
A non-zero vector n perpendicular to a given plane is called normal (normal) for a given plane.
Suppose that in the coordinate space (rectangular coordinate system) Oxyz are given:

It is necessary to make the equation of the plane, which will pass through the point Мₒ perpendicular to the normal n.
In space, choose any arbitrary point anddenote it by M (xy, z). Let the radius vector of any point M (x, y, z) be r = x * i + y * j + z * k, and the radius vector of the point Mₒ (xₒ, yₒ, zₒ) - rₒ = xₒ * i + yₒ * j + zₒ * k. The point M will belong to the given plane if the vector MₒM is perpendicular to the vector n. We write the orthogonality condition using a scalar product:
[MₒM, n] = 0.
Since МₒМ = r – rₒ, the plane vector equation will look like this:
[r - rₒ, n] = 0.
This equation may have another form.For this, the properties of the inner product are used, and the left side of the equation is transformed. [r - rₒ, n] = [r, n] - [rₒ, n]. If [rₒ, n] is denoted as c, then we get the following equation: [r, n] - c = 0 or [r, n] = c, which expresses the constancy of the projections onto the normal vector of the radius vectors of given points that belong to the plane.
Now we can get the coordinate form of the record of the vector equation of our plane [r - rₒ, n] = 0. Since r – rₒ = (x – xₒ) * i + (y – yₒ) * j + (z – zₒ) * k, and n = A * i + B * j + C * k, we have:

It turns out that we form an equation for a plane passing through a point perpendicular to the normal n:
А * (х - хₒ) + В * (у– уₒ) С * (z – zₒ) = 0.
We define two arbitrary points M ′ (x ′, y ′, z ′) and M ″ (x ″, y ″, z ″), as well as the vector a (a ′, a ″, a).
Now we can make an equation of a given plane that will pass through the existing points M ′ and M ″, as well as any point M with coordinates (x, y, z) parallel to the given vector a.
Moreover, the vectors M′M = {xxx ′; yyy ′; zz ′} and M ″ M = {x ″ -x ′; y ″ -y ′; z ″ -z ′} must be coplanar with the vector a = (a ′, a ″, a), which means that (M ′ M, M ″ M, a) = 0.
So, our equation of a plane in space will look like this:
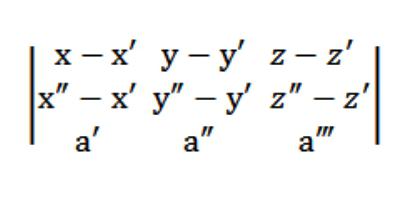
Suppose we have three points:(x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y, z ‴) that do not belong to one straight line. It is necessary to write the equation of the plane passing through the given three points. The theory of geometry asserts that such a plane really exists, only it is unique and inimitable. Since this plane intersects the point (x ′, y ′, z ′), the form of its equation will be as follows:

Here A, B, C are non-zero at the same time. Also, the given plane intersects two more points: (x ″, y ″, z ″) and (x ‴, y ‴, z ‴). In this regard, the following conditions must be met:

Now we can create a homogeneous system of equations (linear) with unknowns u, v, w:

In our case, x, y, or z appears arbitrary.point that satisfies equation (1). Taking into account equation (1) and the system of equations (2) and (3), the system of equations indicated in the figure above is satisfied with the vector N (A, B, C), which is nontrivial. That is why the determinant of this system is zero.
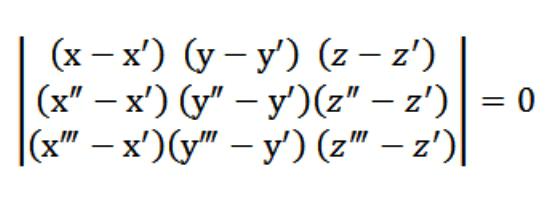
Equation (1), which we got, isthere is a plane equation. It definitely passes through 3 points, and it is easy to check. To do this, we need to expand our determinant on the elements in the first line. From the existing properties of the determinant it follows that our plane simultaneously intersects three initially defined points (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y, z). That is, we decided to set the task.
The dihedral angle representsspatial geometric shape formed by two half-planes, which emanate from one straight line. In other words, it is part of the space that is limited to these half-planes.
Suppose we have two planes with the following equations:
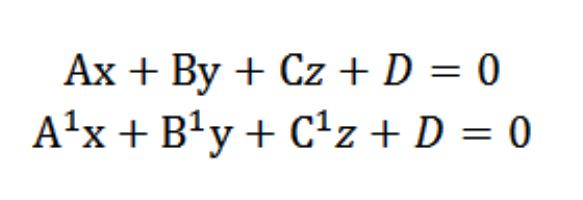
We know that the vectors N = (A, B, C) andN¹ = (А¹, В¹, С¹) are perpendicular according to the given planes. In this regard, the angle φ between the vectors N and N¹ is equal to the angle (dihedral), which is located between these planes. Scalar product has the form:
NN¹ = | N || N¹ | cos φ,
precisely because
cosφ = NN¹ / | N || N¹ | = (AAA + BB¹ + CC¹) / ((√ (А² + В² + С²)) * (√ (А¹) ² + (В¹) ² + (С¹) ²)).
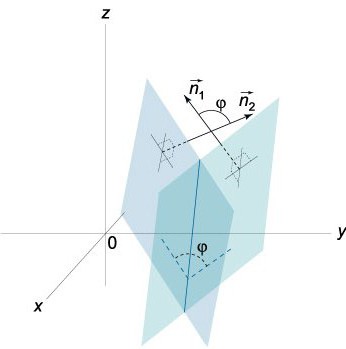
It is enough to take into account that 0≤φ≤π.
In fact, two planes that intersect form two angles (dihedral): φ1 and φ2. Their sum is π (φ1+ φ2= π). As for their cosines, their absolute values are equal, but they differ in signs, that is, cos φ1= -cos φ2. If in equation (0) we replace A, B and C with the numbers -А, -В and -С respectively, then the equation we get will determine the same plane, the only angle φ in the equation cos φ = NN1/ | N || N1| will be replaced by π-φ.
Perpendicular are called planes, betweenwhich angle is 90 degrees. Using the material outlined above, we can find the equation of a plane perpendicular to the other. Suppose we have two planes: Ax + Vu + Cz + D = 0 and A¹x + V¹y + C¹z + D = 0. We can say that they will be perpendicular if cosφ = 0. This means that NN¹ = AA¹ + BB¹ + CC¹ = 0.
Parallel are two planes that do not contain common points.
The condition of parallel planes (their equationsthe same as in the previous paragraph) is that the vectors N and N¹, which are perpendicular to them, are collinear. This means that the following conditions of proportionality are satisfied:
А / А¹ = В / В¹ = С / С¹.
If the proportionality conditions are extended - А / А¹ = В / В¹ = С / С¹ = DD¹,
this indicates that the data planes coincide. And this means that the equations Ax + Wu + Cz + D = 0 and Ak + x + Wu + C +z + D¹ = 0 describe one plane.
Suppose we have a plane P, which is givenby equation (0). It is necessary to find the distance to it from the point with coordinates (xₒ, yₒ, zₒ) = Qₒ. To do this, you need to bring the equation of the plane P in the normal form:
(ρ, v) = p (p≥0).
In this case, ρ (x, y, z) isthe radius vector of our point Q located on P, p is the length of the perpendicular P that was released from the zero point, v is the unit vector that is located in the direction a.

The difference ρ-ρº of the radius vector of some point Q = (x, y, z) belonging to P, as well as the radius vector of a given point Q0= (xₒ, yₒ, zₒ) is such a vector, the absolute value of the projection of which on v equals the distance d, which must be found from Q0= (хₒ, уₒ, zₒ) to П:
D = | (ρ-ρ0, v) |, but
(ρ-ρ0, v) = (ρ, v) - (ρ0, v) = p– (ρ0,at).
So it turns out
d = | (ρ0, v) -p |.
Now you can see to calculate the distance d from Q0 before the plane P, it is necessary to use the normal form of the equation of the plane, transfer to the left side of p, and substitute x, y, z to the last part (xₒ, yₒ, zₒ).
Thus, we find the absolute value of the resulting expression, that is, the desired d.
Using the parameter language, we get the obvious:
d = | Ahₒ + Wooₒ + Czₒ | / √ (А² + В² + С²).
If given point Q0 located on the other side of the plane P, like the origin, then between the vector ρ-ρ0 and v is an obtuse angle, therefore:
d = - (ρ-ρ0, v) = (ρ0, v) –p> 0.
In the case when the point Q0 together with the origin is located on the same side of the P, then the angle is sharp, that is:
d = (ρ-ρ0, v) = p - (ρ0, c)> 0.
The result is that in the first case (ρ0, v)> p, in the second (ρ0, v) The tangent plane to the surface at the tangency point Mº is the plane containing all possible tangents to the curves drawn through this point on the surface. In this form, the equation of the surface F (x, y, z) = 0, the equation of the tangent plane at the tangent point Мº (хº, уº, zº) will look like this: Fx(hº, dº, zº) (x-xº) + Fx(h º, º, z º) (y-º) + Fx(hº, yº, zº) (z-zº) = 0. If you specify the surface in the explicit form z = f (x, y), then the tangent plane will be described by the equation: z-zº = f (хº, уº) (х- хº) + f (хº, уº) (у-уº). В трехмерном пространстве расположена система coordinates (rectangular) Oxyz, are given two planes P ′ and P ″, which intersect and do not coincide. Since any plane located in a rectangular coordinate system is determined by a general equation, we will assume that P ′ and P ″ are given by the equations A′х + B′y + C′z + D ′ = 0 and A ″ x + B ″ y + With ″ z + D ″ = 0. In this case, we have the normal n ′ (A ′, B ′, C ′) of the plane P ′ and the normal n ″ (A ″, B ″, C ″) of the plane P ″. Since our planes are not parallel and do not coincide, these vectors are not collinear. Using the language of mathematics, we can write this condition as follows: n ′ ≠ n ″ (A ′, B ′, C ′) (λ * A ″, λ * B ″, λ * C ″), λϵR. Let the straight line, which lies at the intersection of P ′ and P ″, will be denoted by the letter a, in this case a = P ′ ∩ P ″. a is a line consisting of the set of all points(common) planes P ′ and P ″. This means that the coordinates of any point belonging to the line a must simultaneously satisfy the equations A′x + B′u + C′z + D′ = 0 and A ″ x + B ″ y + C ″ z + D ″ = 0. This means that the coordinates of the point will be a particular solution of the following system of equations:Tangent plane and its equation
Intersection of two planes

The result is that the solution (total) of thisthe system of equations will determine the coordinates of each of the points of the line, which will be the intersection point of P ′ and P ″, and define the line a in the Oxyz coordinate system (rectangular) in space.


























