
To create any programs you need basicalgorithmic constructions. Following is the simplest way to solve problems. It can be used, for example, to work with similar examples. There are other types: branching and looping. About them will be told in this article. But first you need to understand what the algorithm is all about.
The word "algorithm" came from Latin algoritmi.What does it mean? The authentic word came from the name of a mathematician, whose work fell on the 9th century. Thanks to the al-Khwarizmi treatise, mankind was able to get acquainted with the main type of algorithmic construction and generally with a general concept.
Earlier, the form of writing the word "algorithm" was adopted. Now it is used only in some cases.
Algorithm is a process that means changinginitial data, occurring in the form of discrete steps. With this concept every person encounters in life, whoever he is. Algorithms may well be the preparation of tea or food, multiplication or addition, the solution of equations, etc. All household appliances, whose work process is automated, functions at the expense of clear steps prescribed in the memory of the processor. Such algorithms are called household algorithms. There are other types. Consider them.
The basic algorithmic constructions are divided into several types, which will be discussed in this subparagraph. What are they like?
In fact, the algorithm is accurate to the smallestdetails instructions. However, not all such data can be called a described concept. To understand the algorithm of an instruction or not, it should be checked for certain properties.
All the basic algorithmic constructions must have actions that obey them. Let's consider this issue in more detail.
If we completely track the work of the algorithms and theirproperties, you can see that it is not necessary to understand their components, it is quite clear that they correspond to the plan. The correct result will be obtained, even if you just mechanically stick to the necessary actions. From this we can conclude that because of the lack of meaning in the awareness of actions, the algorithm can really be allocated to the implementation of a computer. In other words, for automated devices, this process is necessary.
What properties should the basic algorithmic constructions have for the most accurate work?
If we talk about ways to write algorithms, then we should distinguish the following:
The last point should be clarified.What is a block diagram? This is a linear or non-linear algorithm, the steps of which are recorded using special blocks. They have their own configuration, purpose and function. In the case of such a description, the algorithm is written in block diagrams that are linked together by lines. In them, you must additionally record an action (step).

Some argue that the algorithms have not 3type, and 4. The main algorithmic design: linear, branching, cyclic. What is the reason for this misconception is unclear. However, for simple solving complex problems, the computer uses the algorithms of these three fairly large groups. Consider them.
It should be noted that all the basic algorithmic constructions (follow, branch, cycle) are interrelated with each other, although they can be used separately.
What is needed to create a loop?
Cycles can be deterministic anditerative. The first represent a repetition of actions with the already known number of repetitions. An iteration cycle is one that repeats indefinitely, until the condition becomes true or false.
It is worth remembering that the mainalgorithmic constructs do not apply the basic algorithm. What is it? This concept has long been not found in modern literature, but this does not mean that it does not exist any more. Considering that several branches or repetitions can occur in solving problems, the following conclusion can be singled out. The basic algorithmic constructions (linear, branching, cyclic) are basic. In fact, they represent the "structural unit" of each so-called instruction.
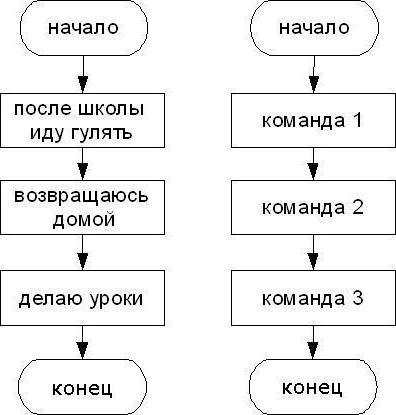
As already clear from the above, the algorithmsthere are linear and nonlinear. Consider the first option. Why is it called that? Everything is extremely simple. The point is that all the actions that are reproduced in the algorithm have a clearly sequential execution, all steps are performed strictly one after another. Typically, such tasks are small and have a low level of complexity.
An example of a linear algorithm can be the process of preparing tea:
Programming the basic algorithmic constructions is quite difficult, but if it is a question of linear algorithms, then it is often very easy to implement them.

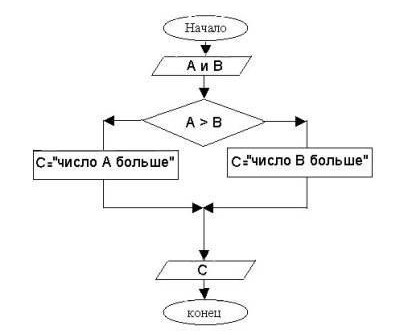
How to understand that the algorithm is branching?It is enough to make sure there is a choice of two or more options, depending on whether the condition is fulfilled or not. Each path is called a branch.
The main feature of the branching algorithm is the existence of a conditional branch. It happens during the verification of the expression to true or false.
As a rule, logical expressions are representedsigns "less", "more", "less than or equal to", "greater than or equal to", "equal", "not equal". Sometimes there are variants where the condition is interconnected with the help of the and (and) and or (or) commands.
An example of such an algorithm may be a solutionof the following problem: if the expression ((x + 3) / 1) is equal to a positive number, output the result to the screen, if negative, tell the user about the error.
It is quite simple to use the basic algorithmic constructions in practice. Branching is one of the most common methods of solution.
A cycle with a counter is a cycle that includesA variable that changes the value with a certain step. The step is set by the user or prescribed by the programmer while writing the collateral. Most languages for this loop use the for statement.
For the program to display two lines 4 times:
It is necessary to create a deterministic cycle. What does it look like? We use the language "Pascal" for better perception of the design.
1. For i: = 1 to 2 do:
- i is the loop counter, it determines the number of repetitions in the loop.
2. Begin (the operator brackets are opened in order for both phrases to be the body of the loop and to be repeated together.)
3. Writeln ('How are you?'):
- the word writeln means the output of a phrase that is in single quotes.
4. Writeln ('Well, thank you').
5. End.
6. i: = i + 1.
As you can see, it is quite easy and even interesting to use the basic algorithmic constructions. Basic algorithms are really widely known, without them it is impossible to write programs.

A loop with a postcondition can be repeatedan indefinite number of actions without inserting operator staples or compound words into them. It will be fulfilled at least once. The loop runs until the condition is false. It stops when the indicators are correct. The algorithm is constructed on this. The basic algorithmic constructions of this type work at this pace.
To implement this cycle, a constructionRepeat A until B. Literally it is translated as "repeat actions, while the condition is false". Accordingly, through A the repetition process itself is expressed, through B - the data, which as a result must take the correct value.
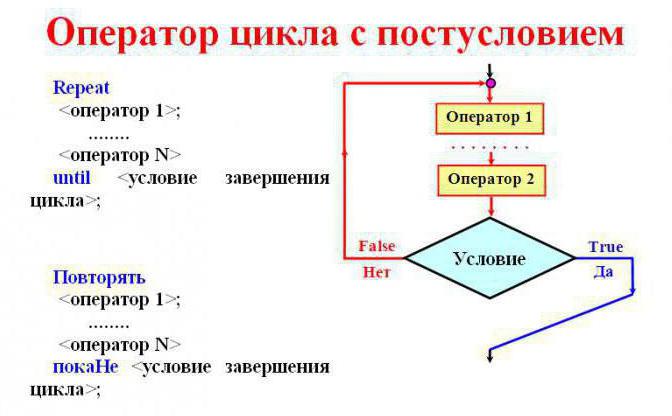
A loop with a postcondition is constructed in such a way thatit is executed at least once in any case. However, there are cases when a cycle is necessary in the case of a particular condition, and if there is no repetition, it should not. Otherwise, the result will be incorrect. It is in this case that a loop with a precondition is used. To create it, you need a "while A do B" construct. The first command is literally translated as "bye". A is a condition, and B is an action that will be repeated. The whole construction means: "as long as the condition is correct, perform the actions".
All the basic algorithmic constructions workonly in certain cases. What are they in the cycle with a precondition? If it is necessary that not one action is repeated, but several, it is worthwhile to use either composite operators or special brackets. The cycle may well not be fulfilled if the condition is not true when entering it. Accordingly, the actions will be repeated if it is correct.

The auxiliary algorithm is used in otherprocesses by specifying only his name. It does not apply to the basic algorithmic constructions. In programming languages, this process of action is called a subroutine. To facilitate the work with the code and subsequently more simple problem solving, each action is combined into one block, which is an auxiliary algorithm. Each of them can be given a name, which allows you to repeatedly refer to it.


























